Note

Go to the end to download the full example code. or to run this example in your browser via Binder

模型复杂度影响#

演示模型复杂度如何影响预测准确性和计算性能。

我们将使用两个数据集：

  • Diabetes dataset 用于回归。 该数据集由糖尿病患者的10项测量值组成。 任务是预测疾病进展；

  • The 20 newsgroups text dataset 用于分类。该数据集由新闻组帖子组成。 任务是预测帖子所讨论的主题（20个主题中的一个）。

我们将对三种不同的估计器建模复杂度的影响：

我们通过选择每个模型中的相关参数来使模型复杂度变化。接下来，我们将测量对计算性能（延迟）和预测能力（MSE或Hamming Loss）的影响。

# 作者：scikit-learn 开发者
# SPDX 许可证标识符：BSD-3-Clause

import time

import matplotlib.pyplot as plt
import numpy as np

from sklearn import datasets
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.linear_model import SGDClassifier
from sklearn.metrics import hamming_loss, mean_squared_error
from sklearn.model_selection import train_test_split
from sklearn.svm import NuSVR

# 初始化随机生成器
np.random.seed(0)

加载数据#

首先我们加载两个数据集。

Note

我们使用 fetch_20newsgroups_vectorized 下载 20 个新闻组数据集。它返回可直接使用的特征。

Note

20类新闻组数据集的 X 是一个稀疏矩阵，而糖尿病数据集的 X 是一个numpy数组。

def generate_data(case):
    """生成回归/分类数据。"""
    if case == "regression":
        X, y = datasets.load_diabetes(return_X_y=True)
        train_size = 0.8
    elif case == "classification":
        X, y = datasets.fetch_20newsgroups_vectorized(subset="all", return_X_y=True)
        train_size = 0.4  # to make the example run faster

    X_train, X_test, y_train, y_test = train_test_split(
        X, y, train_size=train_size, random_state=0
    )

    data = {"X_train": X_train, "X_test": X_test, "y_train": y_train, "y_test": y_test}
    return data


regression_data = generate_data("regression")
classification_data = generate_data("classification")

基准影响#

接下来，我们可以计算参数对给定估计器的影响。在每一轮中，我们将使用新的 changing_param 值设置估计器，并收集预测时间、预测性能和复杂性，以观察这些变化如何影响估计器。我们将使用作为参数传递的 complexity_computer 来计算复杂性。

def benchmark_influence(conf):
    """
        基准测试 `changing_param` 对MSE和延迟的影响。
    """
    prediction_times = []
    prediction_powers = []
    complexities = []
    for param_value in conf["changing_param_values"]:
        conf["tuned_params"][conf["changing_param"]] = param_value
        estimator = conf["estimator"](**conf["tuned_params"])

        print("Benchmarking %s" % estimator)
        estimator.fit(conf["data"]["X_train"], conf["data"]["y_train"])
        conf["postfit_hook"](estimator)
        complexity = conf["complexity_computer"](estimator)
        complexities.append(complexity)
        start_time = time.time()
        for _ in range(conf["n_samples"]):
            y_pred = estimator.predict(conf["data"]["X_test"])
        elapsed_time = (time.time() - start_time) / float(conf["n_samples"])
        prediction_times.append(elapsed_time)
        pred_score = conf["prediction_performance_computer"](
            conf["data"]["y_test"], y_pred
        )
        prediction_powers.append(pred_score)
        print(
            "Complexity: %d | %s: %.4f | Pred. Time: %fs\n"
            % (
                complexity,
                conf["prediction_performance_label"],
                pred_score,
                elapsed_time,
            )
        )
    return prediction_powers, prediction_times, complexities

选择参数#

我们通过创建一个包含所有必要值的字典来选择每个估计器的参数。 changing_param 是在每个估计器中变化的参数名称。 复杂度将由 complexity_label 定义，并使用 complexity_computer 计算。 还请注意，根据估计器类型的不同，我们传递的数据也不同。

def _count_nonzero_coefficients(estimator):
    a = estimator.coef_.toarray()
    return np.count_nonzero(a)


configurations = [
    {
        "estimator": SGDClassifier,
        "tuned_params": {
            "penalty": "elasticnet",
            "alpha": 0.001,
            "loss": "modified_huber",
            "fit_intercept": True,
            "tol": 1e-1,
            "n_iter_no_change": 2,
        },
        "changing_param": "l1_ratio",
        "changing_param_values": [0.25, 0.5, 0.75, 0.9],
        "complexity_label": "non_zero coefficients",
        "complexity_computer": _count_nonzero_coefficients,
        "prediction_performance_computer": hamming_loss,
        "prediction_performance_label": "Hamming Loss (Misclassification Ratio)",
        "postfit_hook": lambda x: x.sparsify(),
        "data": classification_data,
        "n_samples": 5,
    },
    {
        "estimator": NuSVR,
        "tuned_params": {"C": 1e3, "gamma": 2**-15},
        "changing_param": "nu",
        "changing_param_values": [0.05, 0.1, 0.2, 0.35, 0.5],
        "complexity_label": "n_support_vectors",
        "complexity_computer": lambda x: len(x.support_vectors_),
        "data": regression_data,
        "postfit_hook": lambda x: x,
        "prediction_performance_computer": mean_squared_error,
        "prediction_performance_label": "MSE",
        "n_samples": 15,
    },
    {
        "estimator": GradientBoostingRegressor,
        "tuned_params": {
            "loss": "squared_error",
            "learning_rate": 0.05,
            "max_depth": 2,
        },
        "changing_param": "n_estimators",
        "changing_param_values": [10, 25, 50, 75, 100],
        "complexity_label": "n_trees",
        "complexity_computer": lambda x: x.n_estimators,
        "data": regression_data,
        "postfit_hook": lambda x: x,
        "prediction_performance_computer": mean_squared_error,
        "prediction_performance_label": "MSE",
        "n_samples": 15,
    },
]

运行代码并绘制结果

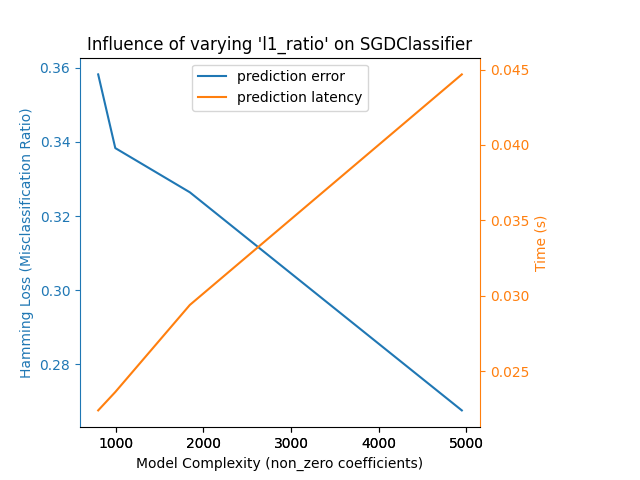
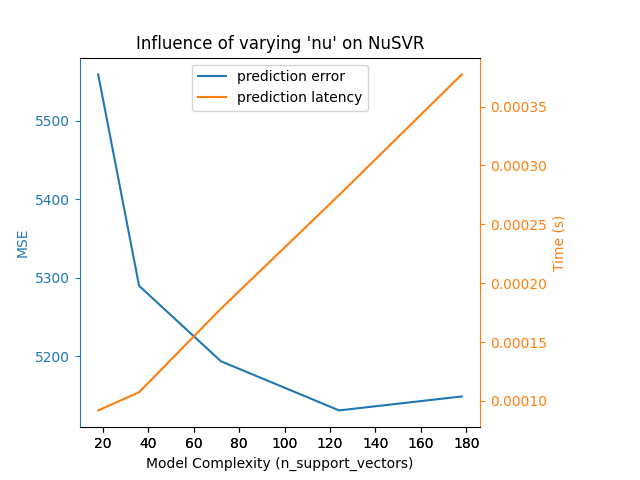
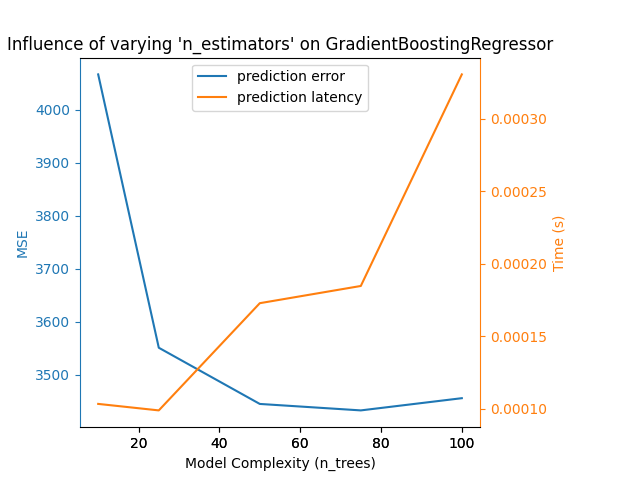
我们定义了运行基准测试所需的所有函数。现在，我们将循环遍历之前定义的不同配置。随后，我们可以分析从基准测试中获得的图表： 放松SGD分类器中的 L1 惩罚会减少预测误差，但会增加训练时间。 我们可以对Nu-SVR的训练时间进行类似的分析，训练时间随着支持向量的数量增加而增加。然而，我们观察到存在一个最佳的支持向量数量，可以减少预测误差。确实，支持向量太少会导致模型欠拟合，而支持向量太多会导致模型过拟合。 对于梯度提升模型也可以得出完全相同的结论。与Nu-SVR的唯一区别是，集成中树的数量过多并不会造成同样的负面影响。

def plot_influence(conf, mse_values, prediction_times, complexities):
    """
    绘制模型复杂度对准确性和延迟的影响。
    """

    fig = plt.figure()
    fig.subplots_adjust(right=0.75)

    # 第一轴（预测误差）
    ax1 = fig.add_subplot(111)
    line1 = ax1.plot(complexities, mse_values, c="tab:blue", ls="-")[0]
    ax1.set_xlabel("Model Complexity (%s)" % conf["complexity_label"])
    y1_label = conf["prediction_performance_label"]
    ax1.set_ylabel(y1_label)

    ax1.spines["left"].set_color(line1.get_color())
    ax1.yaxis.label.set_color(line1.get_color())
    ax1.tick_params(axis="y", colors=line1.get_color())

    # 第二轴（延迟）
    ax2 = fig.add_subplot(111, sharex=ax1, frameon=False)
    line2 = ax2.plot(complexities, prediction_times, c="tab:orange", ls="-")[0]
    ax2.yaxis.tick_right()
    ax2.yaxis.set_label_position("right")
    y2_label = "Time (s)"
    ax2.set_ylabel(y2_label)
    ax1.spines["right"].set_color(line2.get_color())
    ax2.yaxis.label.set_color(line2.get_color())
    ax2.tick_params(axis="y", colors=line2.get_color())

    plt.legend(
        (line1, line2), ("prediction error", "prediction latency"), loc="upper center"
    )

    plt.title(
        "Influence of varying '%s' on %s"
        % (conf["changing_param"], conf["estimator"].__name__)
    )


for conf in configurations:
    prediction_performances, prediction_times, complexities = benchmark_influence(conf)
    plot_influence(conf, prediction_performances, prediction_times, complexities)
plt.show()
  • Influence of varying 'l1_ratio' on SGDClassifier
  • Influence of varying 'nu' on NuSVR
  • Influence of varying 'n_estimators' on GradientBoostingRegressor
Benchmarking SGDClassifier(alpha=0.001, l1_ratio=0.25, loss='modified_huber',
              n_iter_no_change=2, penalty='elasticnet', tol=0.1)
Complexity: 4948 | Hamming Loss (Misclassification Ratio): 0.2675 | Pred. Time: 0.044682s

Benchmarking SGDClassifier(alpha=0.001, l1_ratio=0.5, loss='modified_huber',
              n_iter_no_change=2, penalty='elasticnet', tol=0.1)
Complexity: 1847 | Hamming Loss (Misclassification Ratio): 0.3264 | Pred. Time: 0.029387s

Benchmarking SGDClassifier(alpha=0.001, l1_ratio=0.75, loss='modified_huber',
              n_iter_no_change=2, penalty='elasticnet', tol=0.1)
Complexity: 997 | Hamming Loss (Misclassification Ratio): 0.3383 | Pred. Time: 0.023611s

Benchmarking SGDClassifier(alpha=0.001, l1_ratio=0.9, loss='modified_huber',
              n_iter_no_change=2, penalty='elasticnet', tol=0.1)
Complexity: 802 | Hamming Loss (Misclassification Ratio): 0.3582 | Pred. Time: 0.022392s

Benchmarking NuSVR(C=1000.0, gamma=3.0517578125e-05, nu=0.05)
Complexity: 18 | MSE: 5558.7313 | Pred. Time: 0.000092s

Benchmarking NuSVR(C=1000.0, gamma=3.0517578125e-05, nu=0.1)
Complexity: 36 | MSE: 5289.8022 | Pred. Time: 0.000107s

Benchmarking NuSVR(C=1000.0, gamma=3.0517578125e-05, nu=0.2)
Complexity: 72 | MSE: 5193.8353 | Pred. Time: 0.000178s

Benchmarking NuSVR(C=1000.0, gamma=3.0517578125e-05, nu=0.35)
Complexity: 124 | MSE: 5131.3279 | Pred. Time: 0.000275s

Benchmarking NuSVR(C=1000.0, gamma=3.0517578125e-05)
Complexity: 178 | MSE: 5149.0779 | Pred. Time: 0.000377s

Benchmarking GradientBoostingRegressor(learning_rate=0.05, max_depth=2, n_estimators=10)
Complexity: 10 | MSE: 4066.4812 | Pred. Time: 0.000103s

Benchmarking GradientBoostingRegressor(learning_rate=0.05, max_depth=2, n_estimators=25)
Complexity: 25 | MSE: 3551.1723 | Pred. Time: 0.000099s

Benchmarking GradientBoostingRegressor(learning_rate=0.05, max_depth=2, n_estimators=50)
Complexity: 50 | MSE: 3445.2171 | Pred. Time: 0.000173s

Benchmarking GradientBoostingRegressor(learning_rate=0.05, max_depth=2, n_estimators=75)
Complexity: 75 | MSE: 3433.0358 | Pred. Time: 0.000185s

Benchmarking GradientBoostingRegressor(learning_rate=0.05, max_depth=2)
Complexity: 100 | MSE: 3456.0602 | Pred. Time: 0.000331s

Conclusion#

作为结论，我们可以得出以下见解：

  • 一个更复杂（或更具表现力）的模型将需要更长的训练时间；

  • 一个更复杂的模型并不保证能减少预测误差。

这些方面与模型的泛化能力以及避免模型欠拟合或过拟合有关。

Total running time of the script: (0 minutes 8.516 seconds)

Related examples

变分贝叶斯高斯混合模型的浓度先验类型分析

变分贝叶斯高斯混合模型的浓度先验类型分析

类似然比率用于衡量分类性能

类似然比率用于衡量分类性能

阈值变化对自训练的影响

阈值变化对自训练的影响

使用轮廓分析选择KMeans聚类的簇数

使用轮廓分析选择KMeans聚类的簇数

Gallery generated by Sphinx-Gallery

On this page
Show Source