Note

Go to the end to download the full example code. or to run this example in your browser via Binder

RBF核的显式特征映射近似#

一个展示RBF核特征映射近似的示例。

该示例展示了如何使用 RBFSampler 和 Nystroem 来近似RBF核的特征映射，并在数字数据集上使用SVM进行分类。比较了在原始空间中使用线性SVM、使用近似映射的线性SVM以及使用核化SVM的结果。展示了在不同数量的蒙特卡罗采样（对于使用随机傅里叶特征的 RBFSampler ）和不同大小的训练集子集（对于 Nystroem ）情况下的时间和准确性。

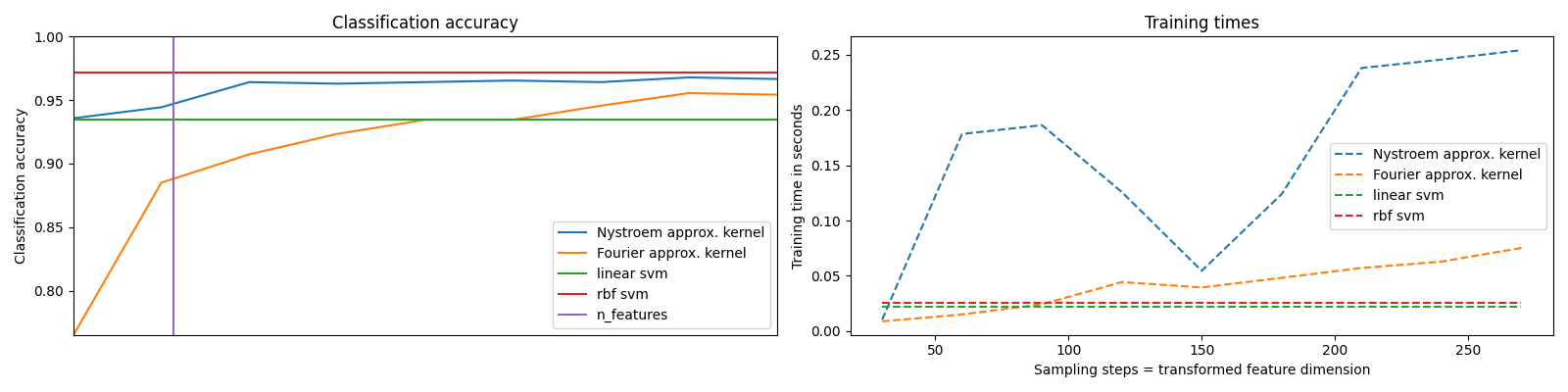
请注意，这里的数据集不够大，无法展示核近似的优势，因为精确的SVM仍然相当快。

采样更多的维度显然会带来更好的分类结果，但代价更高。这意味着在运行时间和准确性之间存在权衡，由参数n_components决定。请注意，通过使用 SGDClassifier 的随机梯度下降法，可以大大加速线性SVM和近似核SVM的求解。这对于核化SVM的情况并不容易实现。

Python 包和数据集导入，加载数据集#

# 作者：scikit-learn 开发者
# SPDX-License-Identifier：BSD-3-Clause

# 标准科学Python导入
from time import time

import matplotlib.pyplot as plt
import numpy as np

# 导入数据集、分类器和性能指标
from sklearn import datasets, pipeline, svm
from sklearn.decomposition import PCA
from sklearn.kernel_approximation import Nystroem, RBFSampler

# The digits dataset
#
#
digits = datasets.load_digits(n_class=9)

时间和准确性图表#

要在这些数据上应用分类器，我们需要将图像展平，将数据转换为 (样本, 特征) 矩阵：

n_samples = len(digits.data)
data = digits.data / 16.0
data -= data.mean(axis=0)

# 我们学习前半部分的数字
data_train, targets_train = (data[: n_samples // 2], digits.target[: n_samples // 2])


# 现在预测后半部分的数字值：
data_test, targets_test = (data[n_samples // 2 :], digits.target[n_samples // 2 :])
# data_test = scaler.transform(data_test)

# 创建一个分类器：支持向量分类器
kernel_svm = svm.SVC(gamma=0.2)
linear_svm = svm.LinearSVC(random_state=42)

# 从核近似和线性支持向量机创建管道
feature_map_fourier = RBFSampler(gamma=0.2, random_state=1)
feature_map_nystroem = Nystroem(gamma=0.2, random_state=1)
fourier_approx_svm = pipeline.Pipeline(
    [
        ("feature_map", feature_map_fourier),
        ("svm", svm.LinearSVC(random_state=42)),
    ]
)

nystroem_approx_svm = pipeline.Pipeline(
    [
        ("feature_map", feature_map_nystroem),
        ("svm", svm.LinearSVC(random_state=42)),
    ]
)

# 使用线性和核SVM进行拟合和预测：

kernel_svm_time = time()
kernel_svm.fit(data_train, targets_train)
kernel_svm_score = kernel_svm.score(data_test, targets_test)
kernel_svm_time = time() - kernel_svm_time

linear_svm_time = time()
linear_svm.fit(data_train, targets_train)
linear_svm_score = linear_svm.score(data_test, targets_test)
linear_svm_time = time() - linear_svm_time

sample_sizes = 30 * np.arange(1, 10)
fourier_scores = []
nystroem_scores = []
fourier_times = []
nystroem_times = []

for D in sample_sizes:
    fourier_approx_svm.set_params(feature_map__n_components=D)
    nystroem_approx_svm.set_params(feature_map__n_components=D)
    start = time()
    nystroem_approx_svm.fit(data_train, targets_train)
    nystroem_times.append(time() - start)

    start = time()
    fourier_approx_svm.fit(data_train, targets_train)
    fourier_times.append(time() - start)

    fourier_score = fourier_approx_svm.score(data_test, targets_test)
    nystroem_score = nystroem_approx_svm.score(data_test, targets_test)
    nystroem_scores.append(nystroem_score)
    fourier_scores.append(fourier_score)

# plot the results:
plt.figure(figsize=(16, 4))
accuracy = plt.subplot(121)
# 第二个y轴用于时间
timescale = plt.subplot(122)

accuracy.plot(sample_sizes, nystroem_scores, label="Nystroem approx. kernel")
timescale.plot(sample_sizes, nystroem_times, "--", label="Nystroem approx. kernel")

accuracy.plot(sample_sizes, fourier_scores, label="Fourier approx. kernel")
timescale.plot(sample_sizes, fourier_times, "--", label="Fourier approx. kernel")

# horizontal lines for exact rbf and linear kernels:
accuracy.plot(
    [sample_sizes[0], sample_sizes[-1]],
    [linear_svm_score, linear_svm_score],
    label="linear svm",
)
timescale.plot(
    [sample_sizes[0], sample_sizes[-1]],
    [linear_svm_time, linear_svm_time],
    "--",
    label="linear svm",
)

accuracy.plot(
    [sample_sizes[0], sample_sizes[-1]],
    [kernel_svm_score, kernel_svm_score],
    label="rbf svm",
)
timescale.plot(
    [sample_sizes[0], sample_sizes[-1]],
    [kernel_svm_time, kernel_svm_time],
    "--",
    label="rbf svm",
)

# 垂直线用于数据集维度 = 64
accuracy.plot([64, 64], [0.7, 1], label="n_features")

# legends and labels
accuracy.set_title("Classification accuracy")
timescale.set_title("Training times")
accuracy.set_xlim(sample_sizes[0], sample_sizes[-1])
accuracy.set_xticks(())
accuracy.set_ylim(np.min(fourier_scores), 1)
timescale.set_xlabel("Sampling steps = transformed feature dimension")
accuracy.set_ylabel("Classification accuracy")
timescale.set_ylabel("Training time in seconds")
accuracy.legend(loc="best")
timescale.legend(loc="best")
plt.tight_layout()
plt.show()

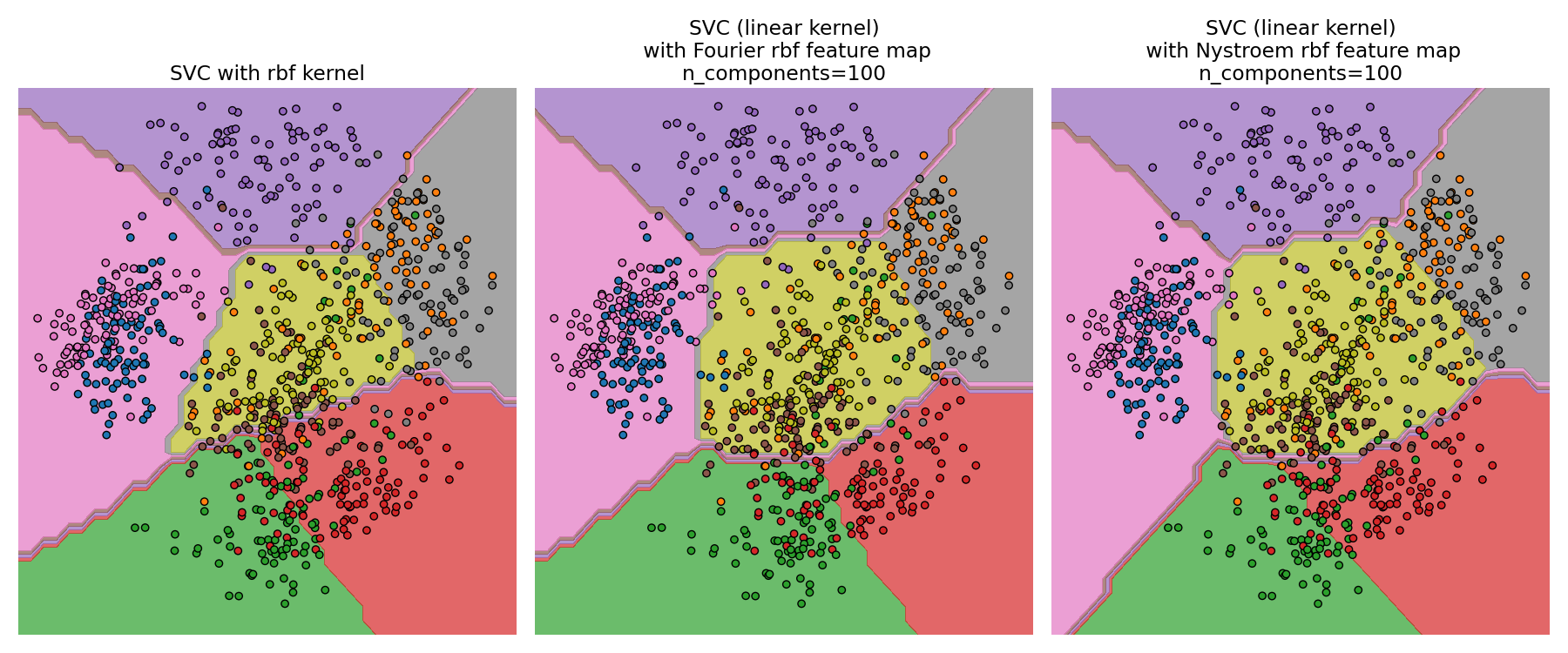
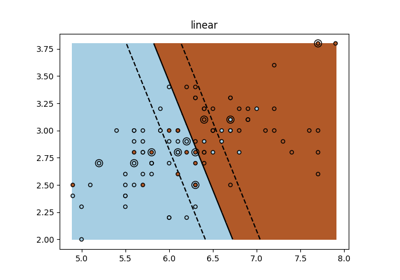
RBF核SVM和线性SVM的决策边界#

第二个图展示了RBF核SVM和带有近似核映射的线性SVM的决策边界。该图显示了分类器投影到数据的前两个主成分上的决策边界。这种可视化应谨慎对待，因为它只是64维决策边界的一个有趣切片。特别要注意的是，一个数据点（用点表示）不一定会被分类到它所在的区域，因为它不会位于前两个主成分所跨越的平面上。 RBFSampler 和:class:Nystroem 的使用在:ref:kernel_approximation 中有详细描述。

# 可视化决策面，投影到数据集的前两个主成分上
pca = PCA(n_components=8, random_state=42).fit(data_train)

X = pca.transform(data_train)

# 沿前两个主成分生成网格
multiples = np.arange(-2, 2, 0.1)
# 沿第一组件的步骤
first = multiples[:, np.newaxis] * pca.components_[0, :]
# 第二部分的步骤
second = multiples[:, np.newaxis] * pca.components_[1, :]
# combine
grid = first[np.newaxis, :, :] + second[:, np.newaxis, :]
flat_grid = grid.reshape(-1, data.shape[1])

# title for the plots
titles = [
    "SVC with rbf kernel",
    "SVC (linear kernel)\n with Fourier rbf feature map\nn_components=100",
    "SVC (linear kernel)\n with Nystroem rbf feature map\nn_components=100",
]

plt.figure(figsize=(18, 7.5))
plt.rcParams.update({"font.size": 14})
# 预测和绘图
for i, clf in enumerate((kernel_svm, nystroem_approx_svm, fourier_approx_svm)):
    # 绘制决策边界。为此，我们将为网格 [x_min, x_max]x[y_min, y_max] 中的每个点分配一个颜色。
    plt.subplot(1, 3, i + 1)
    Z = clf.predict(flat_grid)

    # 将结果放入彩色图中
    Z = Z.reshape(grid.shape[:-1])
    levels = np.arange(10)
    lv_eps = 0.01  # Adjust a mapping from calculated contour levels to color.
    plt.contourf(
        multiples,
        multiples,
        Z,
        levels=levels - lv_eps,
        cmap=plt.cm.tab10,
        vmin=0,
        vmax=10,
        alpha=0.7,
    )
    plt.axis("off")

    # 还要绘制训练点
    plt.scatter(
        X[:, 0],
        X[:, 1],
        c=targets_train,
        cmap=plt.cm.tab10,
        edgecolors=(0, 0, 0),
        vmin=0,
        vmax=10,
    )

    plt.title(titles[i])
plt.tight_layout()
plt.show()