PCA#
- class sklearn.decomposition.PCA(n_components=None, *, copy=True, whiten=False, svd_solver='auto', tol=0.0, iterated_power='auto', n_oversamples=10, power_iteration_normalizer='auto', random_state=None)#
主成分分析(PCA)。
使用奇异值分解(SVD)对数据进行线性降维,以将其投影到低维空间。在应用SVD之前,输入数据被中心化,但不对每个特征进行缩放。
它使用LAPACK实现的全SVD或Halko等人2009年提出的随机截断SVD方法,具体取决于输入数据的形状和要提取的成分数量。
对于稀疏输入,可以使用ARPACK实现的截断SVD(即通过:func:
scipy.sparse.linalg.svds)。或者,可以考虑:class:TruncatedSVD,其中数据不被中心化。请注意,此类仅对某些求解器(如”arpack”和”covariance_eigh”)支持稀疏输入。有关稀疏数据的替代方案,请参见:class:
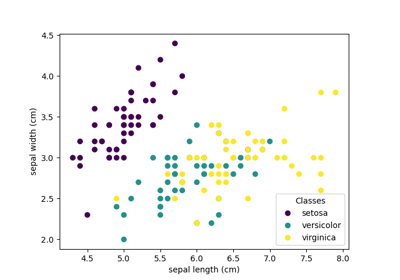
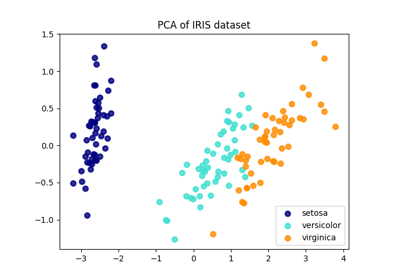
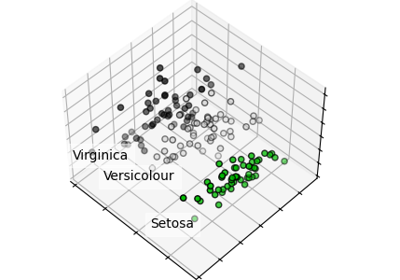
TruncatedSVD。有关使用示例,请参见 使用鸢尾花数据集的PCA示例
更多信息请参阅:ref:
用户指南 <PCA>。- Parameters:
- n_componentsint, float or ‘mle’, default=None
要保留的成分数量。 如果未设置n_components,则保留所有成分:
n_components == min(n_samples, n_features)
如果
n_components == 'mle'且svd_solver == 'full',则使用Minka的MLE猜测维度。使用n_components == 'mle'将解释svd_solver == 'auto'为svd_solver == 'full'。如果
0 < n_components < 1且svd_solver == 'full',则选择成分数量,使得需要解释的方差量大于n_components指定的百分比。如果
svd_solver == 'arpack',成分数量必须严格小于n_features和n_samples的最小值。因此,None情况下的结果为:
n_components == min(n_samples, n_features) - 1
- copybool, default=True
如果为False,传递给fit的数据将被覆盖,运行fit(X).transform(X)将不会产生预期结果,请改用fit_transform(X)。
- whitenbool, default=False
当为True(默认情况下为False)时,
components_向量将乘以n_samples的平方根,然后除以奇异值,以确保输出不相关且成分方差为单位。白化将从变换信号中移除一些信息(成分的相对方差尺度),但有时可以通过使数据符合某些硬编码假设来提高下游估计器的预测准确性。
- svd_solver{‘auto’, ‘full’, ‘covariance_eigh’, ‘arpack’, ‘randomized’}, default=’auto’
- “auto” :
求解器由基于
X.shape和n_components的默认’auto’策略选择:如果输入数据少于1000个特征且样本数量是特征数量的10倍以上,则使用”covariance_eigh”求解器。否则,如果输入数据大于500x500且要提取的成分数量低于数据最小维度的80%,则选择更高效的”randomized”方法。否则,计算精确的全SVD并可选地进行截断。- “full” :
通过
scipy.linalg.svd调用标准LAPACK求解器运行精确的全SVD,并通过后处理选择成分- “covariance_eigh” :
预计算协方差矩阵(在中心化数据上),在协方差矩阵上运行经典的特征值分解,通常使用LAPACK,并通过后处理选择成分。此求解器对于n_samples >> n_features和小n_features非常高效。然而,对于大n_features(需要大量内存 footprint 来具体化协方差矩阵)不可行。另请注意,与”full”求解器相比,此求解器有效地使条件数加倍,因此数值稳定性较差(例如,输入数据具有大范围奇异值时)。
- “arpack” :
通过
scipy.sparse.linalg.svds调用ARPACK求解器运行截断到n_components的SVD。需要严格0 < n_components < min(X.shape)- “randomized” :
通过Halko等人的方法运行随机SVD。
Added in version 0.18.0.
Changed in version 1.5: 添加了’covariance_eigh’求解器。
- tolfloat, default=0.0
由svd_solver == ‘arpack’计算的奇异值的容差。必须在范围[0.0, 无穷大)内。
Added in version 0.18.0.
- iterated_powerint or ‘auto’, default=’auto’
由svd_solver == ‘randomized’计算的幂方法的迭代次数。必须在范围[0, 无穷大)内。
Added in version 0.18.0.
- n_oversamplesint, default=10
此参数仅在
svd_solver="randomized"时相关。它对应于为确保适当条件而额外采样的随机向量数量。有关更多详细信息,请参见:func:~sklearn.utils.extmath.randomized_svd。Added in version 1.1.
- power_iteration_normalizer{‘auto’, ‘QR’, ‘LU’, ‘none’}, default=’auto’
随机SVD求解器的幂迭代归一化器。ARPACK不使用。有关更多详细信息,请参见:func:
~sklearn.utils.extmath.randomized_svd。Added in version 1.1.
- random_stateint, RandomState instance or None, default=None
当使用’arpack’或’randomized’求解器时使用。传递一个int以在多次函数调用中获得可重复的结果。参见:term:
Glossary <random_state>。Added in version 0.18.0.
- Attributes:
- components_ndarray of shape (n_components, n_features)
特征空间中的主轴,表示数据中最大方差的方向。等效地,中心化输入数据的右奇异向量,平行于其特征向量。成分按递减的
explained_variance_排序。- explained_variance_ndarray of shape (n_components,)
每个选定成分解释的方差量。方差估计使用
n_samples - 1自由度。等于X的协方差矩阵的n_components最大特征值。
Added in version 0.18.
- explained_variance_ratio_ndarray of shape (n_components,)
每个选定成分解释的方差百分比。
如果未设置
n_components,则存储所有成分,且比率之和等于1.0。- singular_values_ndarray of shape (n_components,)
每个选定成分对应的奇异值。奇异值等于低维空间中
n_components变量的2-范数。Added in version 0.19.
- mean_ndarray of shape (n_features,)
每个特征的经验均值,从训练集中估计。
等于
X.mean(axis=0)。- n_components_int
估计的成分数量。当n_components设置为’mle’或0到1之间的数字(svd_solver == ‘full’)时,此数量从输入数据中估计。否则,它等于参数n_components,或者在n_components为None时等于n_features和n_samples的较小值。
- n_samples_int
训练数据中的样本数量。
- noise_variance_float
根据Tipping和Bishop 1999年的概率PCA模型估计的噪声协方差。参见C. Bishop的《模式识别与机器学习》12.2.1节p. 574或http://www.miketipping.com/papers/met-mppca.pdf。它需要计算估计的数据协方差和评分样本。
等于X的协方差矩阵的(min(n_features, n_samples) - n_components)最小特征值的平均值。
- n_features_in_int
fit 期间看到的特征数量。
Added in version 0.24.
- feature_names_in_ndarray of shape (
n_features_in_,) fit 期间看到的特征名称。仅当
X的特征名称均为字符串时定义。Added in version 1.0.
See also
KernelPCA核主成分分析。
SparsePCA稀疏主成分分析。
TruncatedSVD使用截断SVD进行降维。
IncrementalPCA增量主成分分析。
References
对于n_components == ‘mle’,此类使用以下方法: Minka, T. P.. “Automatic choice of dimensionality for PCA”. In NIPS, pp. 598-604
实现了以下概率PCA模型: Tipping, M. E., and Bishop, C. M. (1999). “Probabilistic principal component analysis”. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 61(3), 611-622. 通过score和score_samples方法。
对于svd_solver == ‘arpack’,请参见
scipy.sparse.linalg.svds。对于svd_solver == ‘randomized’,请参见: Halko, N., Martinsson, P. G., and Tropp, J. A. (2011). “Finding structure with randomness: Probabilistic algorithms for constructing approximate matrix decompositions”. SIAM review, 53(2), 217-288. 以及 Martinsson, P. G., Rokhlin, V., and Tygert, M. (2011). “A randomized algorithm for the decomposition of matrices”. Applied and Computational Harmonic Analysis, 30(1), 47-68.
Examples
>>> import numpy as np >>> from sklearn.decomposition import PCA >>> X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]]) >>> pca = PCA(n_components=2) >>> pca.fit(X) PCA(n_components=2) >>> print(pca.explained_variance_ratio_) [0.9924... 0.0075...] >>> print(pca.singular_values_) [6.30061... 0.54980...]
>>> pca = PCA(n_components=2, svd_solver='full') >>> pca.fit(X) PCA(n_components=2, svd_solver='full') >>> print(pca.explained_variance_ratio_) [0.9924... 0.00755...] >>> print(pca.singular_values_) [6.30061... 0.54980...]
>>> pca = PCA(n_components=1, svd_solver='arpack') >>> pca.fit(X) PCA(n_components=1, svd_solver='arpack') >>> print(pca.explained_variance_ratio_) [0.99244...] >>> print(pca.singular_values_) [6.30061...]
- fit(X, y=None)#
拟合模型与X。
- Parameters:
- X{array-like, sparse matrix},形状为 (n_samples, n_features)
训练数据,其中
n_samples是样本数量,n_features是特征数量。- y忽略
忽略。
- Returns:
- selfobject
返回实例本身。
- fit_transform(X, y=None)#
拟合模型与X并应用降维于X。
- Parameters:
- X{array-like, sparse matrix},形状为 (n_samples, n_features)
训练数据,其中
n_samples是样本数量,n_features是特征数量。- y忽略
忽略。
- Returns:
- X_newndarray,形状为 (n_samples, n_components)
变换后的值。
Notes
此方法返回一个Fortran顺序的数组。要将其转换为C顺序的数组,请使用 ‘np.ascontiguousarray’。
- get_covariance()#
计算数据与生成模型之间的协方差。
cov = components_.T * S**2 * components_ + sigma2 * eye(n_features)其中 S**2 包含解释的方差,sigma2 包含噪声方差。
- Returns:
- covarray of shape=(n_features, n_features)
数据的估计协方差。
- get_feature_names_out(input_features=None)#
获取转换后的输出特征名称。
输出特征名称将以小写的类名作为前缀。例如,如果转换器输出3个特征,那么输出特征名称将是:
["class_name0", "class_name1", "class_name2"]。- Parameters:
- input_features类似数组的对象或None,默认为None
仅用于验证特征名称与
fit中看到的名称。
- Returns:
- feature_names_outndarray of str对象
转换后的特征名称。
- get_metadata_routing()#
获取此对象的元数据路由。
请查看 用户指南 以了解路由机制的工作原理。
- Returns:
- routingMetadataRequest
MetadataRequest封装的 路由信息。
- get_params(deep=True)#
获取此估计器的参数。
- Parameters:
- deepbool, 默认=True
如果为True,将返回此估计器和包含的子对象(也是估计器)的参数。
- Returns:
- paramsdict
参数名称映射到它们的值。
- get_precision()#
计算数据精度矩阵与生成模型。
等于协方差的逆,但为了提高效率,使用矩阵求逆引理进行计算。
- Returns:
- precisionarray, shape=(n_features, n_features)
数据的估计精度。
- inverse_transform(X)#
将数据转换回其原始空间。
换句话说,返回一个输入
X_original,其转换结果将是 X。- Parameters:
- Xarray-like of shape (n_samples, n_components)
新数据,其中
n_samples是样本数量 且n_components是组件数量。
- Returns:
- X_original array-like of shape (n_samples, n_features)
原始数据,其中
n_samples是样本数量 且n_features是特征数量。
Notes
如果启用了白化,inverse_transform 将计算 精确的逆操作,其中包括反转白化。
- score(X, y=None)#
返回所有样本的平均对数似然。
参见. “模式识别与机器学习” 由 C. Bishop, 12.2.1 p. 574 或 http://www.miketipping.com/papers/met-mppca.pdf
- Parameters:
- X形状为 (n_samples, n_features) 的类数组
数据。
- y忽略
忽略。
- Returns:
- llfloat
当前模型下样本的平均对数似然。
- score_samples(X)#
返回每个样本的对数似然。
参见. “模式识别与机器学习” 由C. Bishop, 12.2.1 p. 574 或 http://www.miketipping.com/papers/met-mppca.pdf
- Parameters:
- X类数组,形状 (n_samples, n_features)
数据。
- Returns:
- llndarray,形状 (n_samples,)
当前模型下每个样本的对数似然。
- set_output(*, transform=None)#
设置输出容器。
请参阅 介绍 set_output API 以了解如何使用API的示例。
- Parameters:
- transform{“default”, “pandas”, “polars”}, 默认=None
配置
transform和fit_transform的输出。"default": 转换器的默认输出格式"pandas": DataFrame 输出"polars": Polars 输出None: 转换配置不变
Added in version 1.4:
"polars"选项已添加。
- Returns:
- self估计器实例
估计器实例。
- set_params(**params)#
设置此估计器的参数。
该方法适用于简单估计器以及嵌套对象(例如
Pipeline)。后者具有形式为<component>__<parameter>的参数,以便可以更新嵌套对象的每个组件。- Parameters:
- **paramsdict
估计器参数。
- Returns:
- selfestimator instance
估计器实例。
- transform(X)#
应用降维到X。
X被投影到从前一个训练集中提取的第一主成分上。
- Parameters:
- X{array-like, sparse matrix},形状为 (n_samples, n_features)
新数据,其中
n_samples是样本数量 和n_features是特征数量。
- Returns:
- X_newarray-like,形状为 (n_samples, n_components)
X在第一主成分上的投影,其中
n_samples是样本数量,n_components是成分数量。
Gallery examples#

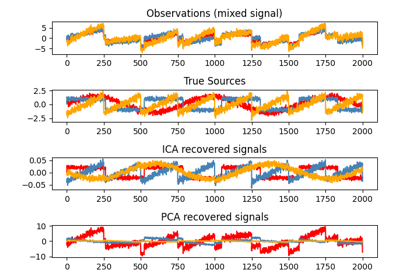
sphx_glr_auto_examples_decomposition_plot_ica_vs_pca.py