johnson_lindenstrauss_min_dim#
- sklearn.random_projection.johnson_lindenstrauss_min_dim(n_samples, *, eps=0.1)#
找到一个“安全”的随机投影组件数量。
随机投影
p引入的失真仅以良好概率在欧几里得空间中将两点之间的距离改变一个因子(1 +- eps)。投影p是如下的 eps-嵌入:(1 - eps) ||u - v||^2 < ||p(u) - p(v)||^2 < (1 + eps) ||u - v||^2
其中 u 和 v 是从形状为 (n_samples, n_features) 的数据集中任意选取的行,eps 在 ]0, 1[ 之间,p 是通过形状为 (n_components, n_features) 的随机高斯 N(0, 1) 矩阵(或稀疏的 Achlioptas 矩阵)进行的投影。
保证 eps-嵌入的最小组件数量由以下公式给出:
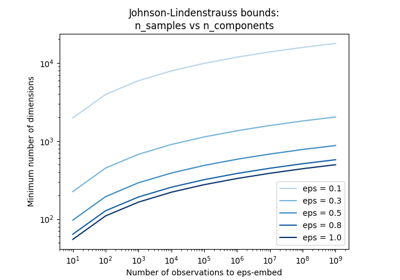
n_components >= 4 log(n_samples) / (eps^2 / 2 - eps^3 / 3)
注意,维度的数量与原始特征的数量无关,而是取决于数据集的大小:数据集越大,eps-嵌入的最小维度越高。
更多信息请参阅 用户指南 。
- Parameters:
- n_samplesint 或 int 的数组
样本数量应为大于 0 的整数。如果给定一个数组,它将逐元素计算安全组件数量。
- epsfloat 或形状为 (n_components,) 的 float 数组, 默认=0.1
最大失真率,范围在 (0, 1) 之间,由 Johnson-Lindenstrauss 引理定义。如果给定一个数组,它将逐元素计算安全组件数量。
- Returns:
- n_componentsint 或 int 的 ndarray
保证以良好概率实现 n_samples 的 eps-嵌入的最小组件数量。
References
Examples
>>> from sklearn.random_projection import johnson_lindenstrauss_min_dim >>> johnson_lindenstrauss_min_dim(1e6, eps=0.5) 663
>>> johnson_lindenstrauss_min_dim(1e6, eps=[0.5, 0.1, 0.01]) array([ 663, 11841, 1112658])
>>> johnson_lindenstrauss_min_dim([1e4, 1e5, 1e6], eps=0.1) array([ 7894, 9868, 11841])