Note

Go to the end to download the full example code. or to run this example in your browser via Binder

主成分回归与偏最小二乘回归#

本示例比较了主成分回归 (PCR) 和偏最小二乘回归 (PLS) 在一个玩具数据集上的表现。我们的目标是说明当目标与数据中某些低方差方向强相关时，PLS 如何能优于 PCR。

PCR 是一个由两步组成的回归器：首先，对训练数据应用 PCA ，可能会进行降维；然后，在转换后的样本上训练一个回归器（例如线性回归器）。在 PCA 中，转换是完全无监督的，这意味着不使用任何关于目标的信息。因此，在某些数据集中，当目标与具有低方差的*方向*强相关时，PCR 的表现可能会很差。实际上，PCA 的降维将数据投影到一个较低维度的空间中，在每个轴上贪婪地最大化投影数据的方差。尽管这些低方差方向对目标具有最强的预测能力，但它们会被丢弃，最终的回归器将无法利用它们。

PLS 既是一个转换器也是一个回归器，它与 PCR 非常相似：它也对样本进行降维，然后对转换后的数据应用线性回归器。与 PCR 的主要区别在于 PLS 转换是有监督的。因此，正如我们将在本示例中看到的，它不会遇到我们刚才提到的问题。

The data#

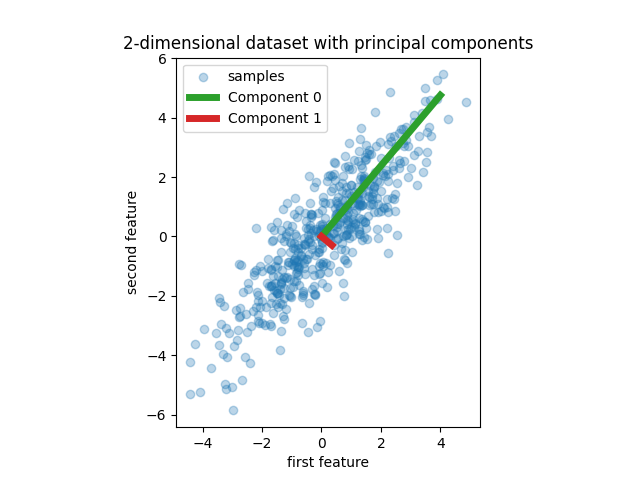
我们首先创建一个包含两个特征的简单数据集。在深入研究PCR和PLS之前，我们拟合一个PCA估计器，以显示该数据集的两个主成分，即解释数据中最大方差的两个方向。

import matplotlib.pyplot as plt
import numpy as np

from sklearn.decomposition import PCA

rng = np.random.RandomState(0)
n_samples = 500
cov = [[3, 3], [3, 4]]
X = rng.multivariate_normal(mean=[0, 0], cov=cov, size=n_samples)
pca = PCA(n_components=2).fit(X)


plt.scatter(X[:, 0], X[:, 1], alpha=0.3, label="samples")
for i, (comp, var) in enumerate(zip(pca.components_, pca.explained_variance_)):
    comp = comp * var  # scale component by its variance explanation power
    plt.plot(
        [0, comp[0]],
        [0, comp[1]],
        label=f"Component {i}",
        linewidth=5,
        color=f"C{i + 2}",
    )
plt.gca().set(
    aspect="equal",
    title="2-dimensional dataset with principal components",
    xlabel="first feature",
    ylabel="second feature",
)
plt.legend()
plt.show()

2-dimensional dataset with principal components

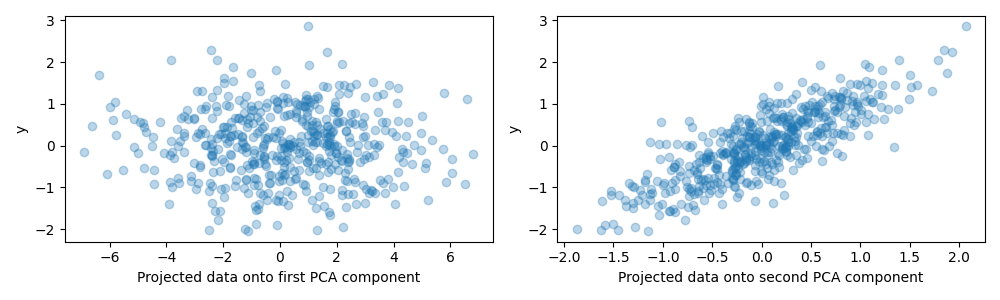
为了这个示例的目的，我们现在定义目标 y ，使其与方差较小的方向强烈相关。为此，我们将 X 投影到第二个分量上，并添加一些噪声。

y = X.dot(pca.components_[1]) + rng.normal(size=n_samples) / 2

fig, axes = plt.subplots(1, 2, figsize=(10, 3))

axes[0].scatter(X.dot(pca.components_[0]), y, alpha=0.3)
axes[0].set(xlabel="Projected data onto first PCA component", ylabel="y")
axes[1].scatter(X.dot(pca.components_[1]), y, alpha=0.3)
axes[1].set(xlabel="Projected data onto second PCA component", ylabel="y")
plt.tight_layout()
plt.show()

对一个成分的投影和预测能力#

我们现在创建两个回归器：PCR 和 PLS，并且为了演示的目的，我们将组件数量设置为 1。在将数据输入到 PCR 的 PCA 步骤之前，我们首先对其进行标准化，这是良好实践所推荐的。PLS 估计器具有内置的缩放功能。

对于这两种模型，我们将投影到第一个成分上的数据与目标进行对比绘图。在这两种情况下，这些投影数据都是回归器将用作训练数据的内容。

from sklearn.cross_decomposition import PLSRegression
from sklearn.decomposition import PCA
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=rng)

pcr = make_pipeline(StandardScaler(), PCA(n_components=1), LinearRegression())
pcr.fit(X_train, y_train)
pca = pcr.named_steps["pca"]  # retrieve the PCA step of the pipeline

pls = PLSRegression(n_components=1)
pls.fit(X_train, y_train)

fig, axes = plt.subplots(1, 2, figsize=(10, 3))
axes[0].scatter(pca.transform(X_test), y_test, alpha=0.3, label="ground truth")
axes[0].scatter(
    pca.transform(X_test), pcr.predict(X_test), alpha=0.3, label="predictions"
)
axes[0].set(
    xlabel="Projected data onto first PCA component", ylabel="y", title="PCR / PCA"
)
axes[0].legend()
axes[1].scatter(pls.transform(X_test), y_test, alpha=0.3, label="ground truth")
axes[1].scatter(
    pls.transform(X_test), pls.predict(X_test), alpha=0.3, label="predictions"
)
axes[1].set(xlabel="Projected data onto first PLS component", ylabel="y", title="PLS")
axes[1].legend()
plt.tight_layout()
plt.show()

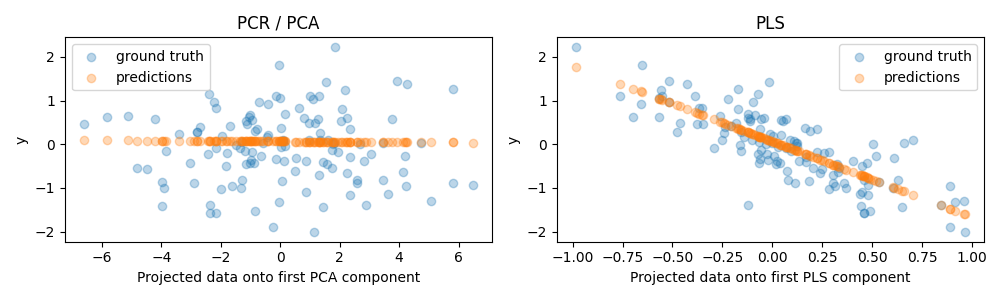
正如预期的那样，PCR 的无监督 PCA 变换舍弃了第二个成分，即方差最低的方向，尽管它是最具预测性的方向。这是因为 PCA 是一种完全无监督的变换，导致投影数据对目标的预测能力较低。

另一方面，PLS 回归器能够捕捉到方差最小方向的影响，这要归功于其在转换过程中使用了目标信息：它可以识别出这个方向实际上是最具预测性的。我们注意到，第一个 PLS 组件与目标呈负相关，这源于特征向量的符号是任意的。

我们还打印了两个估计量的R平方得分，这进一步确认了在这种情况下，PLS比PCR更好。负的R平方表明，PCR的表现比仅仅预测目标均值的回归器还要差。

print(f"PCR r-squared {pcr.score(X_test, y_test):.3f}")
print(f"PLS r-squared {pls.score(X_test, y_test):.3f}")

PCR r-squared -0.026
PLS r-squared 0.658

最后需要指出的是，使用2个成分的PCR表现与PLS一样好：这是因为在这种情况下，PCR能够利用对目标具有最大预测能力的第二个成分。

pca_2 = make_pipeline(PCA(n_components=2), LinearRegression())
pca_2.fit(X_train, y_train)
print(f"PCR r-squared with 2 components {pca_2.score(X_test, y_test):.3f}")