Note
Go to the end to download the full example code. or to run this example in your browser via Binder
调整决策阈值以适应成本敏感学习#
一旦分类器训练完成,predict 方法的输出将根据 decision_function 或 predict_proba 的输出进行阈值化,输出类别标签预测。对于二元分类器,默认阈值定义为后验概率估计为0.5或决策分数为0.0。
然而,这种默认策略很可能不是当前任务的最优策略。在这里,我们使用“Statlog”德国信用数据集 [1] 来说明一个用例。在该数据集中,任务是预测一个人信用是“好”还是“坏”。此外,还提供了一个成本矩阵,指定了误分类的成本。具体来说,将“坏”信用误分类为“好”信用的成本平均是将“好”信用误分类为“坏”信用的五倍。
我们使用 TunedThresholdClassifierCV 来选择决策函数的截断点,以最小化提供的业务成本。
在示例的第二部分,我们通过考虑信用卡交易中的欺诈检测问题进一步扩展了这种方法:在这种情况下,业务指标取决于每笔交易的金额。
参考文献
具有恒定收益和成本的成本敏感学习#
在本节中,我们展示了在每个混淆矩阵条目的收益和成本都是恒定的情况下,如何在成本敏感学习中使用 TunedThresholdClassifierCV 。我们使用 [2] 中提出的问题,并使用 “Statlog” 德国信用数据集 [1]。
“Statlog” 德国信用数据集
我们从OpenML获取德国信用数据集。
import sklearn
from sklearn.datasets import fetch_openml
sklearn.set_config(transform_output="pandas")
german_credit = fetch_openml(data_id=31, as_frame=True, parser="pandas")
X, y = german_credit.data, german_credit.target
我们检查 X 中可用的特征类型。
X.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 1000 entries, 0 to 999
Data columns (total 20 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 checking_status 1000 non-null category
1 duration 1000 non-null int64
2 credit_history 1000 non-null category
3 purpose 1000 non-null category
4 credit_amount 1000 non-null int64
5 savings_status 1000 non-null category
6 employment 1000 non-null category
7 installment_commitment 1000 non-null int64
8 personal_status 1000 non-null category
9 other_parties 1000 non-null category
10 residence_since 1000 non-null int64
11 property_magnitude 1000 non-null category
12 age 1000 non-null int64
13 other_payment_plans 1000 non-null category
14 housing 1000 non-null category
15 existing_credits 1000 non-null int64
16 job 1000 non-null category
17 num_dependents 1000 non-null int64
18 own_telephone 1000 non-null category
19 foreign_worker 1000 non-null category
dtypes: category(13), int64(7)
memory usage: 69.9 KB
许多特征是分类的,通常是字符串编码的。在开发预测模型时,我们需要对这些类别进行编码。让我们检查一下目标。
y.value_counts()
class
good 700
bad 300
Name: count, dtype: int64
另一个观察结果是数据集不平衡。在评估我们的预测模型时,我们需要小心,并使用适合这种情况的一系列指标。
此外,我们观察到目标是字符串编码的。一些指标(例如精确度和召回率)需要提供感兴趣的标签,也称为“正标签”。在这里,我们定义我们的目标是预测一个样本是否是“坏”信用。
pos_label, neg_label = "bad", "good"
为了进行分析,我们使用单次分层拆分来拆分数据集。
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, random_state=0)
我们已经准备好设计我们的预测模型和相关的评估策略。
评估指标#
在本节中,我们定义了一组稍后会使用的指标。为了观察调整截断点的效果,我们使用受试者工作特征(ROC)曲线和精确率-召回率曲线来评估预测模型。因此,这些图上报告的值分别是ROC曲线的真正例率(TPR,也称为召回率或敏感性)和假正例率(FPR,也称为特异性),以及精确率-召回率曲线的精确率和召回率。
根据这四个指标,scikit-learn 并未提供用于计算 FPR 的评分器。因此,我们需要定义一个小的自定义函数来计算它。
from sklearn.metrics import confusion_matrix
def fpr_score(y, y_pred, neg_label, pos_label):
cm = confusion_matrix(y, y_pred, labels=[neg_label, pos_label])
tn, fp, _, _ = cm.ravel()
tnr = tn / (tn + fp)
return 1 - tnr
正如前面所述,“正标签”并未定义为值“1”,并且使用此非标准值调用某些指标会引发错误。我们需要向指标提供“正标签”的指示。
因此,我们需要使用 make_scorer 定义一个 scikit-learn 评分器,并传递相关信息。我们将所有自定义评分器存储在一个字典中。要使用它们,我们需要传递拟合的模型、数据以及我们希望评估预测模型的目标。
from sklearn.metrics import make_scorer, precision_score, recall_score
tpr_score = recall_score # TPR and recall are the same metric
scoring = {
"precision": make_scorer(precision_score, pos_label=pos_label),
"recall": make_scorer(recall_score, pos_label=pos_label),
"fpr": make_scorer(fpr_score, neg_label=neg_label, pos_label=pos_label),
"tpr": make_scorer(tpr_score, pos_label=pos_label),
}
此外,原始研究 [1] 定义了一个自定义的业务指标。我们称任何旨在量化预测(正确或错误)如何影响在特定应用环境中部署给定机器学习模型的业务价值的指标函数为“业务指标”。对于我们的信用预测任务,作者提供了一个自定义的成本矩阵,该矩阵编码了将“坏”信用分类为“好”平均成本是相反情况的5倍:对于金融机构来说,不向不会违约的潜在客户提供信用(因此错过了一个本来会偿还信用并支付利息的好客户)的成本要低于向会违约的客户提供信用的成本。
我们定义了一个加权混淆矩阵并返回总体成本的 Python 函数。
import numpy as np
def credit_gain_score(y, y_pred, neg_label, pos_label):
cm = confusion_matrix(y, y_pred, labels=[neg_label, pos_label])
# 混淆矩阵的行表示观测类的计数,列表示预测类的计数。请注意,这里我们将“坏”视为正类(第二行和第二列)。Scikit-learn 模型选择工具期望我们遵循“越高越好”的惯例,因此以下收益矩阵为两种预测错误分配了负收益(成本):
# - 每个假阳性(“好”信用被标记为“坏”)的收益为 -1,
# - 每个假阴性(“坏”信用被标记为“好”)的收益为 -5,
# 在此度量中,真正类和真负类被分配为零收益。
#
# 请注意,理论上,如果我们的模型经过校准且数据集具有代表性且足够大,我们不需要调整阈值,而可以安全地将其设置为成本比1/5,正如Elkan论文[2]_中的公式(2)所述。
gain_matrix = np.array(
[
[0, -1], # -1 gain for false positives
[-5, 0], # -5 gain for false negatives
]
)
return np.sum(cm * gain_matrix)
scoring["credit_gain"] = make_scorer(
credit_gain_score, neg_label=neg_label, pos_label=pos_label
)
香草预测模型#
我们使用 HistGradientBoostingClassifier 作为预测模型,该模型本身可以处理分类特征和缺失值。
from sklearn.ensemble import HistGradientBoostingClassifier
model = HistGradientBoostingClassifier(
categorical_features="from_dtype", random_state=0
).fit(X_train, y_train)
model
我们使用ROC曲线和精确率-召回率曲线来评估预测模型的性能。
import matplotlib.pyplot as plt
from sklearn.metrics import PrecisionRecallDisplay, RocCurveDisplay
fig, axs = plt.subplots(nrows=1, ncols=2, figsize=(14, 6))
PrecisionRecallDisplay.from_estimator(
model, X_test, y_test, pos_label=pos_label, ax=axs[0], name="GBDT"
)
axs[0].plot(
scoring["recall"](model, X_test, y_test),
scoring["precision"](model, X_test, y_test),
marker="o",
markersize=10,
color="tab:blue",
label="Default cut-off point at a probability of 0.5",
)
axs[0].set_title("Precision-Recall curve")
axs[0].legend()
RocCurveDisplay.from_estimator(
model,
X_test,
y_test,
pos_label=pos_label,
ax=axs[1],
name="GBDT",
plot_chance_level=True,
)
axs[1].plot(
scoring["fpr"](model, X_test, y_test),
scoring["tpr"](model, X_test, y_test),
marker="o",
markersize=10,
color="tab:blue",
label="Default cut-off point at a probability of 0.5",
)
axs[1].set_title("ROC curve")
axs[1].legend()
_ = fig.suptitle("Evaluation of the vanilla GBDT model")
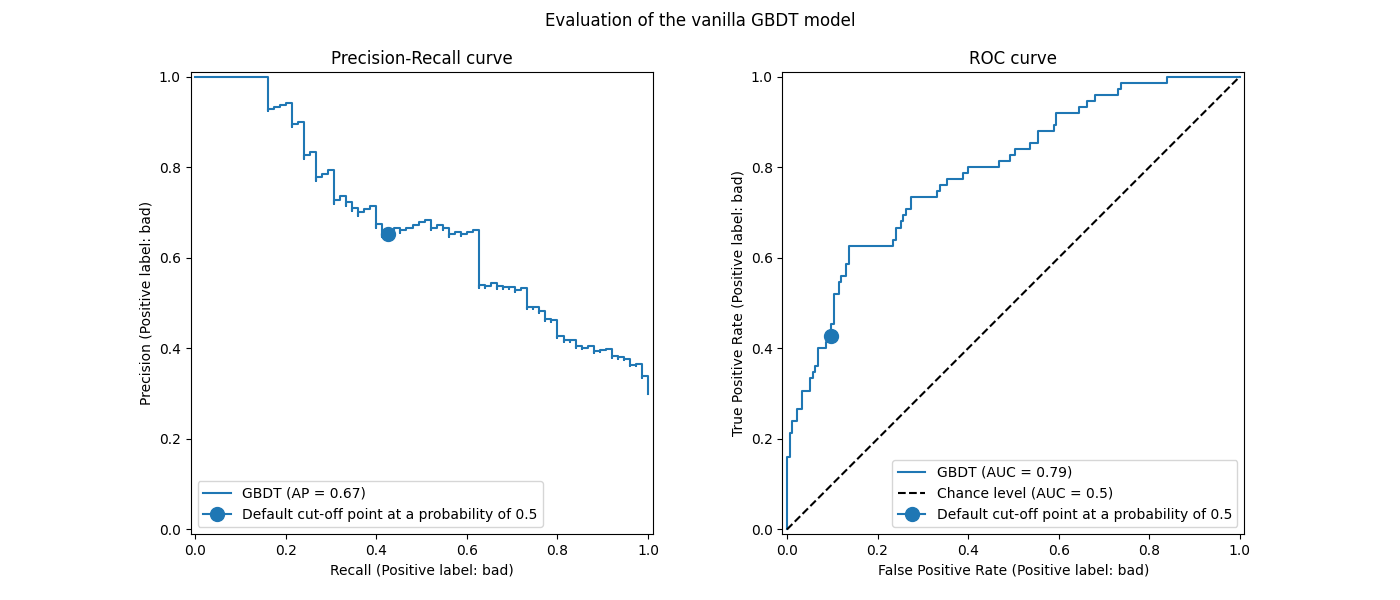
我们回顾一下,这些曲线提供了关于预测模型在不同截断点上的统计性能的见解。对于精确率-召回率曲线,报告的指标是精确率和召回率;对于ROC曲线,报告的指标是TPR(与召回率相同)和FPR。
这里,不同的截断点对应于介于0和1之间的不同后验概率估计水平。默认情况下, model.predict 使用概率估计为0.5的截断点。此类截断点的指标在曲线上用蓝点表示:它对应于使用 model.predict 时模型的统计性能。
然而,我们记得最初的目标是根据业务指标最小化成本(或最大化收益)。我们可以计算业务指标的值:
print(f"Business defined metric: {scoring['credit_gain'](model, X_test, y_test)}")
Business defined metric: -232
在这个阶段,我们还不知道是否有其他截断点可以带来更大的收益。为了找到最优的截断点,我们需要使用业务指标计算所有可能截断点的成本收益,并选择最佳的那个。手动实现这一策略可能相当繁琐,但 TunedThresholdClassifierCV 类可以帮助我们。它会自动计算所有可能截断点的成本收益,并针对 scoring 进行优化。
调整截止点
我们使用 TunedThresholdClassifierCV 来调整截断点。我们需要提供要优化的业务指标以及正标签。在内部,选择最佳截断点以通过交叉验证最大化业务指标。默认情况下,使用5折分层交叉验证。
from sklearn.model_selection import TunedThresholdClassifierCV
tuned_model = TunedThresholdClassifierCV(
estimator=model,
scoring=scoring["credit_gain"],
store_cv_results=True, # necessary to inspect all results
)
tuned_model.fit(X_train, y_train)
print(f"{tuned_model.best_threshold_=:0.2f}")
tuned_model.best_threshold_=0.02
我们绘制了原始模型和调优模型的ROC曲线和精确率-召回率曲线。 同时,我们绘制了每个模型将使用的截断点。因为我们稍后会重用相同的代码,所以我们定义了一个生成图表的函数。
def plot_roc_pr_curves(vanilla_model, tuned_model, *, title):
fig, axs = plt.subplots(nrows=1, ncols=3, figsize=(21, 6))
linestyles = ("dashed", "dotted")
markerstyles = ("o", ">")
colors = ("tab:blue", "tab:orange")
names = ("Vanilla GBDT", "Tuned GBDT")
for idx, (est, linestyle, marker, color, name) in enumerate(
zip((vanilla_model, tuned_model), linestyles, markerstyles, colors, names)
):
decision_threshold = getattr(est, "best_threshold_", 0.5)
PrecisionRecallDisplay.from_estimator(
est,
X_test,
y_test,
pos_label=pos_label,
linestyle=linestyle,
color=color,
ax=axs[0],
name=name,
)
axs[0].plot(
scoring["recall"](est, X_test, y_test),
scoring["precision"](est, X_test, y_test),
marker,
markersize=10,
color=color,
label=f"Cut-off point at probability of {decision_threshold:.2f}",
)
RocCurveDisplay.from_estimator(
est,
X_test,
y_test,
pos_label=pos_label,
linestyle=linestyle,
color=color,
ax=axs[1],
name=name,
plot_chance_level=idx == 1,
)
axs[1].plot(
scoring["fpr"](est, X_test, y_test),
scoring["tpr"](est, X_test, y_test),
marker,
markersize=10,
color=color,
label=f"Cut-off point at probability of {decision_threshold:.2f}",
)
axs[0].set_title("Precision-Recall curve")
axs[0].legend()
axs[1].set_title("ROC curve")
axs[1].legend()
axs[2].plot(
tuned_model.cv_results_["thresholds"],
tuned_model.cv_results_["scores"],
color="tab:orange",
)
axs[2].plot(
tuned_model.best_threshold_,
tuned_model.best_score_,
"o",
markersize=10,
color="tab:orange",
label="Optimal cut-off point for the business metric",
)
axs[2].legend()
axs[2].set_xlabel("Decision threshold (probability)")
axs[2].set_ylabel("Objective score (using cost-matrix)")
axs[2].set_title("Objective score as a function of the decision threshold")
fig.suptitle(title)
title = "Comparison of the cut-off point for the vanilla and tuned GBDT model"
plot_roc_pr_curves(model, tuned_model, title=title)
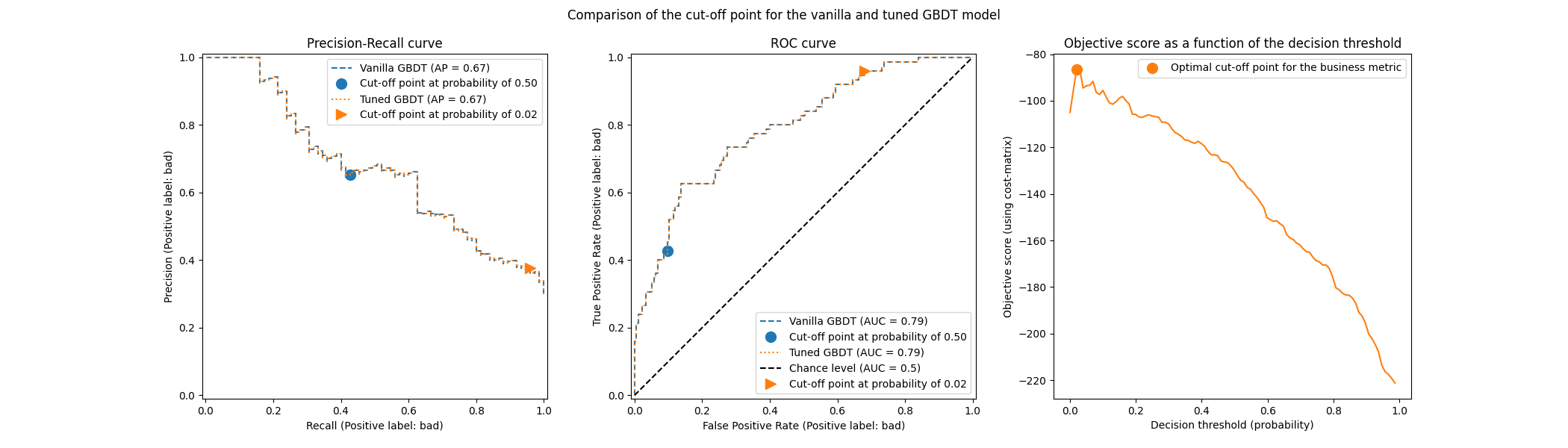
第一个需要注意的是,这两个分类器具有完全相同的ROC和精确率-召回率曲线。这是预期的,因为默认情况下,分类器是在相同的训练数据上进行拟合的。在后面的部分中,我们将更详细地讨论有关模型重新拟合和交叉验证的可用选项。
第二点需要注意的是,原始模型和调优模型的截断点不同。为了理解调优模型为何选择这个截断点,我们可以查看右侧的图表,该图表绘制了与我们的业务指标完全相同的目标分数。我们看到,最佳阈值对应于目标分数的最大值。这个最大值出现在一个远低于0.5的决策阈值处:调优模型在显著降低精度的代价下,享有更高的召回率:调优模型更倾向于将更多个体预测为“坏”类别。
我们现在可以检查选择这个截止点是否会在测试集上带来更好的得分:
print(f"Business defined metric: {scoring['credit_gain'](tuned_model, X_test, y_test)}")
Business defined metric: -134
我们观察到,调整决策阈值几乎使我们的业务收益提高了2倍。
关于模型重拟合和交叉验证的考虑事项
在上述实验中,我们使用了 TunedThresholdClassifierCV 的默认设置。特别地,截断点是通过5折分层交叉验证进行调整的。此外,一旦选择了截断点,基础预测模型会在整个训练数据上重新拟合。
这两种策略可以通过提供 refit 和 cv 参数来更改。例如,可以提供一个已拟合的 estimator 并设置 cv="prefit" ,在这种情况下,截断点是在拟合时提供的整个数据集上找到的。此外,通过设置 refit=False ,基础分类器不会被重新拟合。在这里,我们可以尝试进行这样的实验。
model.fit(X_train, y_train)
tuned_model.set_params(cv="prefit", refit=False).fit(X_train, y_train)
print(f"{tuned_model.best_threshold_=:0.2f}")
tuned_model.best_threshold_=0.28
然后,我们用之前相同的方法评估我们的模型:
title = "Tuned GBDT model without refitting and using the entire dataset"
plot_roc_pr_curves(model, tuned_model, title=title)
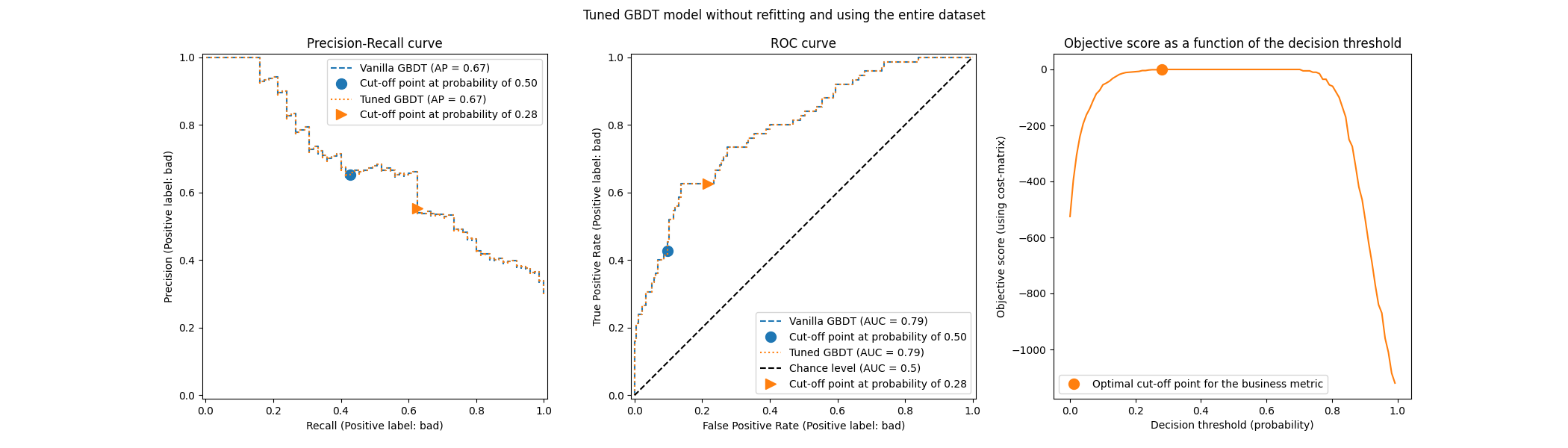
我们观察到最佳截断点与之前实验中发现的不同。如果我们看右侧的图表,可以看到业务收益在很大范围的决策阈值上有一个接近最优0收益的大平台。这种行为是过拟合的症状。由于我们禁用了交叉验证,我们在与模型训练集相同的集合上调整了截断点,这就是观察到过拟合的原因。
因此,应谨慎使用此选项。需要确保在拟合时提供给 TunedThresholdClassifierCV 的数据与用于训练基础分类器的数据不同。当仅仅是为了在一个全新的验证集上调整预测模型而不进行昂贵的完全重拟合时,这种情况有时会发生。
当交叉验证成本过高时,一个潜在的替代方法是通过向 cv 参数提供一个 [0, 1] 范围内的浮点数来使用单次训练-测试拆分。它将数据分成训练集和测试集。让我们来探讨这个选项:
tuned_model.set_params(cv=0.75).fit(X_train, y_train)
title = "Tuned GBDT model without refitting and using the entire dataset"
plot_roc_pr_curves(model, tuned_model, title=title)
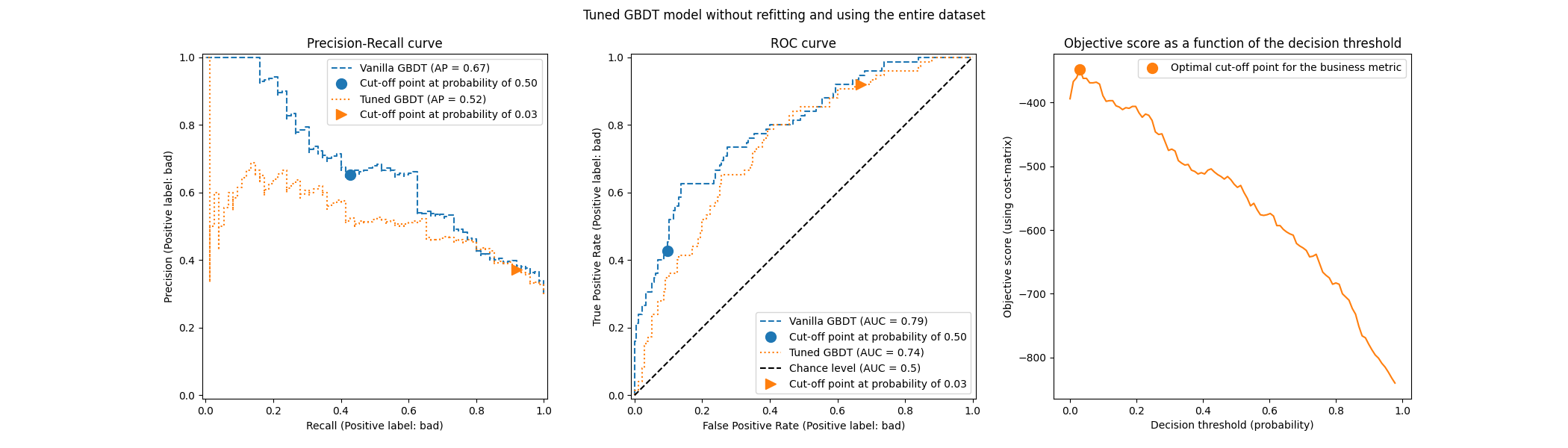
关于截断点,我们观察到最优值与多次重复交叉验证情况相似。然而,请注意,单次分割并未考虑拟合/预测过程的变异性,因此我们无法知道截断点是否存在任何方差。重复交叉验证平均化了这一效应。
另一个观察点涉及调整后的模型的ROC曲线和精确率-召回率曲线。正如预期的那样,这些曲线与原始模型的曲线有所不同,因为我们在拟合过程中使用了提供的数据子集来训练基础分类器,并保留了一个验证集用于调整截断点。
当收益和成本不恒定时的成本敏感学习
正如文献 [2] 所述,收益和成本在现实世界问题中通常不是恒定的。 在本节中,我们使用与文献 [2] 中类似的示例来解决信用卡交易记录中欺诈检测的问题。
信用卡数据集
credit_card = fetch_openml(data_id=1597, as_frame=True, parser="pandas")
credit_card.frame.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 284807 entries, 0 to 284806
Data columns (total 30 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 V1 284807 non-null float64
1 V2 284807 non-null float64
2 V3 284807 non-null float64
3 V4 284807 non-null float64
4 V5 284807 non-null float64
5 V6 284807 non-null float64
6 V7 284807 non-null float64
7 V8 284807 non-null float64
8 V9 284807 non-null float64
9 V10 284807 non-null float64
10 V11 284807 non-null float64
11 V12 284807 non-null float64
12 V13 284807 non-null float64
13 V14 284807 non-null float64
14 V15 284807 non-null float64
15 V16 284807 non-null float64
16 V17 284807 non-null float64
17 V18 284807 non-null float64
18 V19 284807 non-null float64
19 V20 284807 non-null float64
20 V21 284807 non-null float64
21 V22 284807 non-null float64
22 V23 284807 non-null float64
23 V24 284807 non-null float64
24 V25 284807 non-null float64
25 V26 284807 non-null float64
26 V27 284807 non-null float64
27 V28 284807 non-null float64
28 Amount 284807 non-null float64
29 Class 284807 non-null category
dtypes: category(1), float64(29)
memory usage: 63.3 MB
该数据集包含信用卡记录信息,其中一些是欺诈的,另一些是合法的。因此,目标是预测信用卡记录是否为欺诈。
columns_to_drop = ["Class"]
data = credit_card.frame.drop(columns=columns_to_drop)
target = credit_card.frame["Class"].astype(int)
首先,我们检查数据集的类别分布。
target.value_counts(normalize=True)
Class
0 0.998273
1 0.001727
Name: proportion, dtype: float64
该数据集高度不平衡,欺诈交易仅占数据的0.17%。由于我们有兴趣训练一个机器学习模型,我们还应确保在少数类中有足够的样本来训练模型。
target.value_counts()
Class
0 284315
1 492
Name: count, dtype: int64
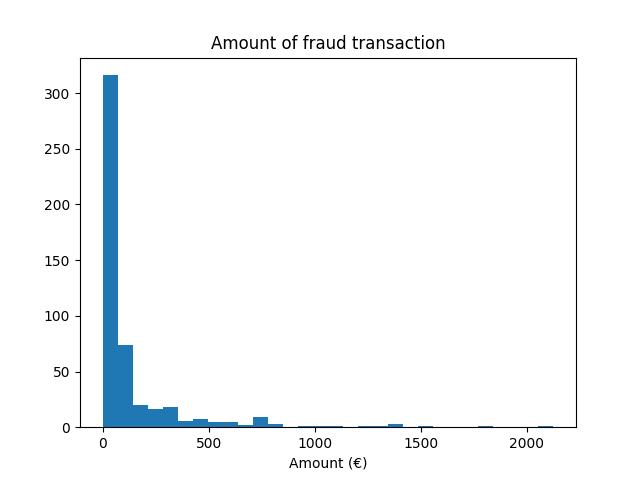
我们观察到我们有大约500个样本,这在训练机器学习模型所需的样本数量中属于较少的。此外,除了目标分布,我们还检查了欺诈交易金额的分布。
fraud = target == 1
amount_fraud = data["Amount"][fraud]
_, ax = plt.subplots()
ax.hist(amount_fraud, bins=30)
ax.set_title("Amount of fraud transaction")
_ = ax.set_xlabel("Amount (€)")
解决业务指标问题
现在,我们创建一个依赖于每笔交易金额的业务指标。我们类似于[2]_定义成本矩阵。接受一笔合法交易会带来交易金额2%的收益。然而,接受一笔欺诈交易会导致交易金额的损失。如[2]_所述,拒绝(欺诈和合法交易)相关的收益和损失定义起来并不简单。在这里,我们定义拒绝一笔合法交易估计为损失5欧元,而拒绝一笔欺诈交易估计为收益50欧元。因此,我们定义以下函数来计算给定决策的总收益:
def business_metric(y_true, y_pred, amount):
mask_true_positive = (y_true == 1) & (y_pred == 1)
mask_true_negative = (y_true == 0) & (y_pred == 0)
mask_false_positive = (y_true == 0) & (y_pred == 1)
mask_false_negative = (y_true == 1) & (y_pred == 0)
fraudulent_refuse = mask_true_positive.sum() * 50
fraudulent_accept = -amount[mask_false_negative].sum()
legitimate_refuse = mask_false_positive.sum() * -5
legitimate_accept = (amount[mask_true_negative] * 0.02).sum()
return fraudulent_refuse + fraudulent_accept + legitimate_refuse + legitimate_accept
从这个业务指标中,我们创建了一个scikit-learn评分器,该评分器在给定一个已拟合的分类器和一个测试集的情况下计算业务指标。在这方面,我们使用了:func:~sklearn.metrics.make_scorer 工厂。变量 amount 是传递给评分器的附加元数据,我们需要使用:ref:metadata routing <metadata_routing> 来考虑这些信息。
sklearn.set_config(enable_metadata_routing=True)
business_scorer = make_scorer(business_metric).set_score_request(amount=True)
因此,在此阶段,我们观察到交易金额被使用了两次:一次作为特征来训练我们的预测模型,一次作为元数据来计算业务指标,从而计算我们模型的统计性能。当作为特征使用时,我们只需要在 data 中有一列包含每笔交易的金额。要将此信息用作元数据,我们需要有一个外部变量,可以传递给评分器或模型,内部将此元数据路由到评分器。所以让我们创建这个变量。
amount = credit_card.frame["Amount"].to_numpy()
from sklearn.model_selection import train_test_split
data_train, data_test, target_train, target_test, amount_train, amount_test = (
train_test_split(
data, target, amount, stratify=target, test_size=0.5, random_state=42
)
)
我们首先评估一些基准策略作为参考。请记住,类别“0”是合法类别,类别“1”是欺诈类别。
from sklearn.dummy import DummyClassifier
always_accept_policy = DummyClassifier(strategy="constant", constant=0)
always_accept_policy.fit(data_train, target_train)
benefit = business_scorer(
always_accept_policy, data_test, target_test, amount=amount_test
)
print(f"Benefit of the 'always accept' policy: {benefit:,.2f}€")
Benefit of the 'always accept' policy: 221,445.07€
一个将所有交易视为合法的策略将产生约220,000欧元的利润。我们对一个预测所有交易为欺诈的分类器进行相同的评估。
always_reject_policy = DummyClassifier(strategy="constant", constant=1)
always_reject_policy.fit(data_train, target_train)
benefit = business_scorer(
always_reject_policy, data_test, target_test, amount=amount_test
)
print(f"Benefit of the 'always reject' policy: {benefit:,.2f}€")
Benefit of the 'always reject' policy: -698,490.00€
这样的政策将导致灾难性的损失:大约670,000欧元。这是预料之中的,因为绝大多数交易都是合法的,而该政策将以不小的代价拒绝这些交易。
一个能够根据每笔交易调整接受/拒绝决策的预测模型,理想情况下应该使我们获得的利润超过我们最佳恒定基线策略的220,000欧元。
我们从默认决策阈值为0.5的逻辑回归模型开始。在这里,我们通过一个适当的评分规则(对数损失)来调整逻辑回归的超参数 C ,以确保模型的 predict_proba 方法返回的概率预测尽可能准确,而不考虑决策阈值的选择。
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import GridSearchCV
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
logistic_regression = make_pipeline(StandardScaler(), LogisticRegression())
param_grid = {"logisticregression__C": np.logspace(-6, 6, 13)}
model = GridSearchCV(logistic_regression, param_grid, scoring="neg_log_loss").fit(
data_train, target_train
)
model
print(
"Benefit of logistic regression with default threshold: "
f"{business_scorer(model, data_test, target_test, amount=amount_test):,.2f}€"
)
Benefit of logistic regression with default threshold: 244,919.87€
业务指标显示,我们的预测模型在默认决策阈值下,已经在利润方面超过了基线,使用它来接受或拒绝交易而不是接受所有交易已经是有利的。
调整决策阈值
现在的问题是:我们的模型对于我们想要做的决策类型来说是否是最优的?
到目前为止,我们还没有优化决策阈值。我们使用 TunedThresholdClassifierCV 来根据我们的业务评分器优化决策。为了避免嵌套交叉验证,我们将使用在之前网格搜索中找到的最佳估计器。
tuned_model = TunedThresholdClassifierCV(
estimator=model.best_estimator_,
scoring=business_scorer,
thresholds=100,
n_jobs=2,
)
由于我们的业务评分器需要每笔交易的金额,我们需要在 fit 方法中传递这些信息。TunedThresholdClassifierCV 负责自动将这些元数据分派给底层评分器。
tuned_model.fit(data_train, target_train, amount=amount_train)
我们观察到调整后的决策阈值远离默认的0.5:
print(f"Tuned decision threshold: {tuned_model.best_threshold_:.2f}")
Tuned decision threshold: 0.03
print(
"Benefit of logistic regression with a tuned threshold: "
f"{business_scorer(tuned_model, data_test, target_test, amount=amount_test):,.2f}€"
)
Benefit of logistic regression with a tuned threshold: 249,433.39€
我们观察到,调整决策阈值可以提高部署模型时的预期利润——这一点由业务指标表明。因此,只要有可能,优化决策阈值以符合业务指标是有价值的。
手动设置决策阈值而不是调整它
在前面的例子中,我们使用了:class:~sklearn.model_selection.TunedThresholdClassifierCV 来找到最佳决策阈值。然而,在某些情况下,我们可能对手头的问题有一些先验知识,并且我们可能愿意手动设置决策阈值。
类 FixedThresholdClassifier 允许我们手动设置决策阈值。在预测时,它的行为与之前调优的模型相同,但在拟合过程中不进行搜索。
在这里,我们将重用上一节中找到的决策阈值来创建一个新模型,并检查它是否给出相同的结果。
from sklearn.model_selection import FixedThresholdClassifier
model_fixed_threshold = FixedThresholdClassifier(
estimator=model, threshold=tuned_model.best_threshold_, prefit=True
).fit(data_train, target_train)
business_score = business_scorer(
model_fixed_threshold, data_test, target_test, amount=amount_test
)
print(f"Benefit of logistic regression with a tuned threshold: {business_score:,.2f}€")
Benefit of logistic regression with a tuned threshold: 249,433.39€
我们观察到我们获得了完全相同的结果,但拟合过程要快得多,因为我们没有进行任何超参数搜索。
最后,(平均)业务指标本身的估计可能不可靠,特别是当少数类的数据点数量非常少时。通过对历史数据(离线评估)进行业务指标的交叉验证来估计的任何业务影响,理想情况下都应该通过对实时数据(在线评估)进行A/B测试来确认。但是请注意,A/B测试模型超出了scikit-learn库本身的范围。
Total running time of the script: (0 minutes 18.739 seconds)
Related examples