Note

Go to the end to download the full example code. or to run this example in your browser via Binder

比较交叉分解方法#

各种交叉分解算法的简单用法：

PLSCanonical
PLS回归，具有多变量响应，又称PLS2
PLS回归，具有单变量响应，又称PLS1
CCA

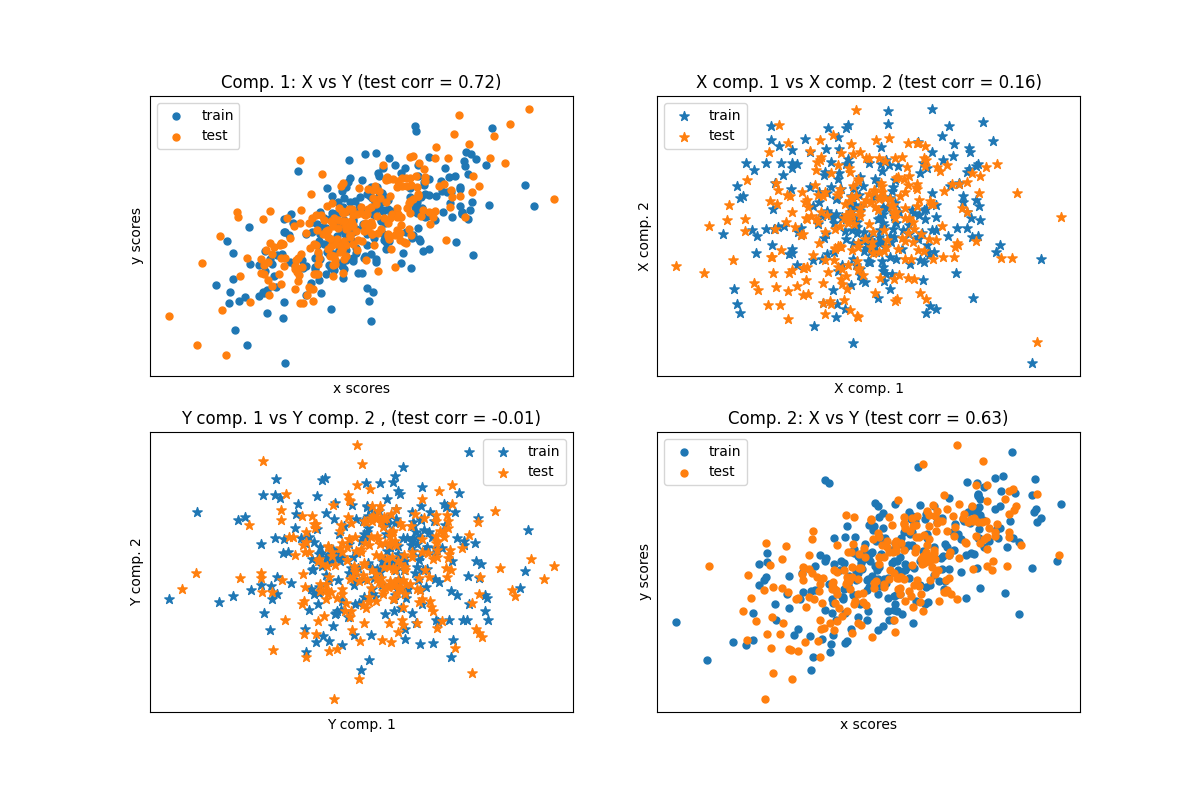
给定两个多变量协变的二维数据集X和Y，PLS提取“协方差方向”，即解释两个数据集之间最大共享方差的各个成分。这在**散点矩阵图**显示中很明显：数据集X和数据集Y中的成分1是最大相关的（点位于第一对角线附近）。对于两个数据集中的成分2也是如此，然而，不同成分之间跨数据集的相关性较弱：点云非常球形。

基于数据集的潜在变量模型#

import numpy as np

n = 500
# 2 latents vars:
l1 = np.random.normal(size=n)
l2 = np.random.normal(size=n)

latents = np.array([l1, l1, l2, l2]).T
X = latents + np.random.normal(size=4 * n).reshape((n, 4))
Y = latents + np.random.normal(size=4 * n).reshape((n, 4))

X_train = X[: n // 2]
Y_train = Y[: n // 2]
X_test = X[n // 2 :]
Y_test = Y[n // 2 :]

print("Corr(X)")
print(np.round(np.corrcoef(X.T), 2))
print("Corr(Y)")
print(np.round(np.corrcoef(Y.T), 2))

Corr(X)
[[ 1.    0.49 -0.05 -0.04]
 [ 0.49  1.   -0.01 -0.01]
 [-0.05 -0.01  1.    0.48]
 [-0.04 -0.01  0.48  1.  ]]
Corr(Y)
[[ 1.    0.53  0.03 -0.02]
 [ 0.53  1.    0.   -0.03]
 [ 0.03  0.    1.    0.5 ]
 [-0.02 -0.03  0.5   1.  ]]

规范（对称）PLS#

转换数据#

from sklearn.cross_decomposition import PLSCanonical

plsca = PLSCanonical(n_components=2)
plsca.fit(X_train, Y_train)
X_train_r, Y_train_r = plsca.transform(X_train, Y_train)
X_test_r, Y_test_r = plsca.transform(X_test, Y_test)

分数的散点图#

import matplotlib.pyplot as plt

# 在对角线上绘制每个成分的X与Y得分
plt.figure(figsize=(12, 8))
plt.subplot(221)
plt.scatter(X_train_r[:, 0], Y_train_r[:, 0], label="train", marker="o", s=25)
plt.scatter(X_test_r[:, 0], Y_test_r[:, 0], label="test", marker="o", s=25)
plt.xlabel("x scores")
plt.ylabel("y scores")
plt.title(
    "Comp. 1: X vs Y (test corr = %.2f)"
    % np.corrcoef(X_test_r[:, 0], Y_test_r[:, 0])[0, 1]
)
plt.xticks(())
plt.yticks(())
plt.legend(loc="best")

plt.subplot(224)
plt.scatter(X_train_r[:, 1], Y_train_r[:, 1], label="train", marker="o", s=25)
plt.scatter(X_test_r[:, 1], Y_test_r[:, 1], label="test", marker="o", s=25)
plt.xlabel("x scores")
plt.ylabel("y scores")
plt.title(
    "Comp. 2: X vs Y (test corr = %.2f)"
    % np.corrcoef(X_test_r[:, 1], Y_test_r[:, 1])[0, 1]
)
plt.xticks(())
plt.yticks(())
plt.legend(loc="best")

# 非对角线图组件 1 对 2 的 X 和 Y
plt.subplot(222)
plt.scatter(X_train_r[:, 0], X_train_r[:, 1], label="train", marker="*", s=50)
plt.scatter(X_test_r[:, 0], X_test_r[:, 1], label="test", marker="*", s=50)
plt.xlabel("X comp. 1")
plt.ylabel("X comp. 2")
plt.title(
    "X comp. 1 vs X comp. 2 (test corr = %.2f)"
    % np.corrcoef(X_test_r[:, 0], X_test_r[:, 1])[0, 1]
)
plt.legend(loc="best")
plt.xticks(())
plt.yticks(())

plt.subplot(223)
plt.scatter(Y_train_r[:, 0], Y_train_r[:, 1], label="train", marker="*", s=50)
plt.scatter(Y_test_r[:, 0], Y_test_r[:, 1], label="test", marker="*", s=50)
plt.xlabel("Y comp. 1")
plt.ylabel("Y comp. 2")
plt.title(
    "Y comp. 1 vs Y comp. 2 , (test corr = %.2f)"
    % np.corrcoef(Y_test_r[:, 0], Y_test_r[:, 1])[0, 1]
)
plt.legend(loc="best")
plt.xticks(())
plt.yticks(())
plt.show()

Comp. 1: X vs Y (test corr = 0.72), Comp. 2: X vs Y (test corr = 0.63), X comp. 1 vs X comp. 2 (test corr = 0.16), Y comp. 1 vs Y comp. 2 , (test corr = -0.01)

PLS 回归，多变量响应，又称 PLS2#

from sklearn.cross_decomposition import PLSRegression

n = 1000
q = 3
p = 10
X = np.random.normal(size=n * p).reshape((n, p))
B = np.array([[1, 2] + [0] * (p - 2)] * q).T
# 每个 Yj = 1*X1 + 2*X2 + 噪声
Y = np.dot(X, B) + np.random.normal(size=n * q).reshape((n, q)) + 5

pls2 = PLSRegression(n_components=3)
pls2.fit(X, Y)
print("True B (such that: Y = XB + Err)")
print(B)
# 比较 pls2.coef_ 和 B
print("Estimated B")
print(np.round(pls2.coef_, 1))
pls2.predict(X)

True B (such that: Y = XB + Err)
[[1 1 1]
 [2 2 2]
 [0 0 0]
 [0 0 0]
 [0 0 0]
 [0 0 0]
 [0 0 0]
 [0 0 0]
 [0 0 0]
 [0 0 0]]
Estimated B
[[ 1.   2.  -0.1 -0.  -0.  -0.  -0.  -0.1  0.  -0. ]
 [ 1.   1.9 -0.  -0.   0.   0.1 -0.   0.  -0.  -0. ]
 [ 1.   1.9 -0.  -0.  -0.   0.  -0.  -0.  -0.  -0. ]]

array([[4.46260781, 4.3792903 , 4.36836896],
       [5.22294138, 5.07398425, 5.06453542],
       [3.2416229 , 3.5337111 , 3.43197656],
       ...,
       [8.8168107 , 8.67329602, 8.61637485],
       [9.55912109, 9.37260612, 9.3419536 ],
       [6.80361268, 6.99998367, 6.88026638]])

PLS 回归，具有单变量响应，又称 PLS1#

n = 1000
p = 10
X = np.random.normal(size=n * p).reshape((n, p))
y = X[:, 0] + 2 * X[:, 1] + np.random.normal(size=n * 1) + 5
pls1 = PLSRegression(n_components=3)
pls1.fit(X, y)
# 请注意，组件的数量超过了1（y的维度）
print("Estimated betas")
print(np.round(pls1.coef_, 1))

Estimated betas
[[ 0.9  2.  -0.  -0.  -0.  -0.1  0.  -0.   0.  -0. ]]

CCA（对称消减的PLS模式B）#

from sklearn.cross_decomposition import CCA

cca = CCA(n_components=2)
cca.fit(X_train, Y_train)
X_train_r, Y_train_r = cca.transform(X_train, Y_train)
X_test_r, Y_test_r = cca.transform(X_test, Y_test)