Note

Go to the end to download the full example code. or to run this example in your browser via Binder

稳健的协方差估计和马氏距离的相关性#

本示例展示了在高斯分布数据上使用马氏距离进行协方差估计。

对于高斯分布数据，可以使用马氏距离计算观测值 \(x_i\) 到分布模式的距离：

\[d_{(\mu,\Sigma)}(x_i)^2 = (x_i - \mu)^T\Sigma^{-1}(x_i - \mu)\]

其中 \(\mu\) 和 \(\Sigma\) 分别是底层高斯分布的均值和协方差。

在实际操作中，\(\mu\) 和 \(\Sigma\) 被一些估计值所替代。标准的协方差最大似然估计（MLE）对数据集中异常值非常敏感，因此，下游的马氏距离也会受到影响。最好使用稳健的协方差估计器，以确保估计对数据集中的“错误”观测值具有抵抗力，并且计算出的马氏距离能够准确反映观测值的真实组织。

最小协方差行列式估计器（MCD）是一种稳健的、高破坏点（即它可以用于估计高度污染数据集的协方差矩阵，最多可容忍 \(\frac{n_\text{samples}-n_\text{features}-1}{2}\) 个异常值）的协方差估计器。MCD 的思想是找到 \(\frac{n_\text{samples}+n_\text{features}+1}{2}\) 个观测值，其经验协方差具有最小的行列式，从而产生一个“纯净”的观测子集，从中计算标准的均值和协方差估计。MCD 由 P.J.Rousseuw 在 [1] 中引入。

本示例说明了马氏距离如何受到异常数据的影响。当使用基于标准协方差 MLE 的马氏距离时，从污染分布中抽取的观测值与来自真实高斯分布的观测值无法区分。使用基于 MCD 的马氏距离，这两种群体变得可以区分。相关应用包括异常值检测、观测值排序和聚类。

Note

另请参见稳健与经验协方差估计

参考文献

生成数据#

首先，我们生成一个包含125个样本和2个特征的数据集。两个特征均为均值为0的高斯分布，但特征1的标准差为2，特征2的标准差为1。接下来，将25个样本替换为高斯异常值样本，其中特征1的标准差为1，特征2的标准差为7。

import numpy as np

# 为了获得一致的结果
np.random.seed(7)

n_samples = 125
n_outliers = 25
n_features = 2

# 生成形状为 (125, 2) 的高斯数据
gen_cov = np.eye(n_features)
gen_cov[0, 0] = 2.0
X = np.dot(np.random.randn(n_samples, n_features), gen_cov)
# 添加一些离群值
outliers_cov = np.eye(n_features)
outliers_cov[np.arange(1, n_features), np.arange(1, n_features)] = 7.0
X[-n_outliers:] = np.dot(np.random.randn(n_outliers, n_features), outliers_cov)

结果比较#

下面，我们将基于MCD和MLE的协方差估计器拟合到我们的数据，并打印估计的协方差矩阵。请注意，基于MLE的估计器对特征2的估计方差（7.5）比MCD稳健估计器（1.2）高得多。这表明基于MCD的稳健估计器对异常样本更具抵抗力，这些异常样本被设计为在特征2中具有更大的方差。

import matplotlib.pyplot as plt

from sklearn.covariance import EmpiricalCovariance, MinCovDet

# 拟合一个MCD稳健估计器到数据
robust_cov = MinCovDet().fit(X)
# 拟合一个最大似然估计器到数据
emp_cov = EmpiricalCovariance().fit(X)
print(
    "Estimated covariance matrix:\nMCD (Robust):\n{}\nMLE:\n{}".format(
        robust_cov.covariance_, emp_cov.covariance_
    )
)

Estimated covariance matrix:
MCD (Robust):
[[ 3.26253567e+00 -3.06695631e-03]
 [-3.06695631e-03  1.22747343e+00]]
MLE:
[[ 3.23773583 -0.24640578]
 [-0.24640578  7.51963999]]

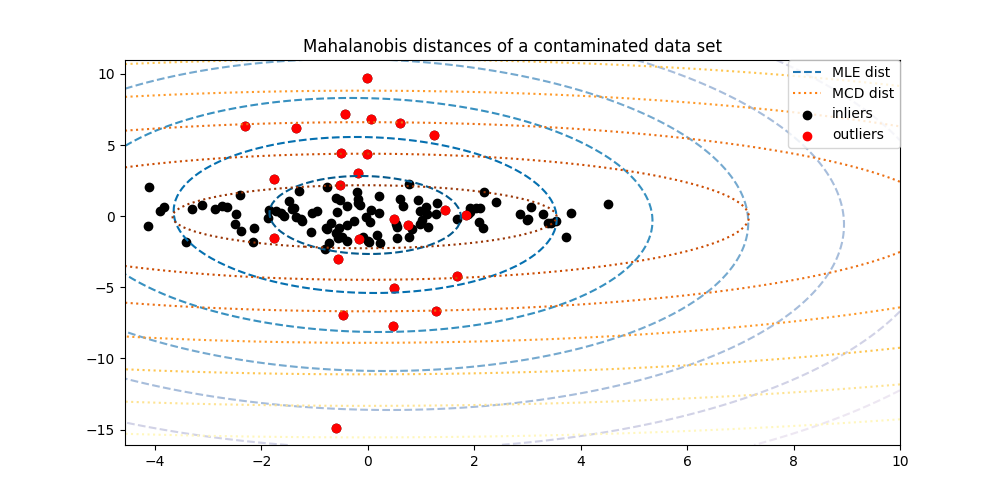
为了更好地可视化差异，我们绘制了由两种方法计算的马氏距离的等高线。请注意，基于稳健MCD的马氏距离更好地拟合了内点（黑点），而基于MLE的距离则更容易受到异常值（红点）的影响。

import matplotlib.lines as mlines

fig, ax = plt.subplots(figsize=(10, 5))
# 绘制数据集
inlier_plot = ax.scatter(X[:, 0], X[:, 1], color="black", label="inliers")
outlier_plot = ax.scatter(
    X[:, 0][-n_outliers:], X[:, 1][-n_outliers:], color="red", label="outliers"
)
ax.set_xlim(ax.get_xlim()[0], 10.0)
ax.set_title("Mahalanobis distances of a contaminated data set")

# 创建特征1和特征2值的网格
xx, yy = np.meshgrid(
    np.linspace(plt.xlim()[0], plt.xlim()[1], 100),
    np.linspace(plt.ylim()[0], plt.ylim()[1], 100),
)
zz = np.c_[xx.ravel(), yy.ravel()]
# 计算基于最大似然估计的网格马氏距离
mahal_emp_cov = emp_cov.mahalanobis(zz)
mahal_emp_cov = mahal_emp_cov.reshape(xx.shape)
emp_cov_contour = plt.contour(
    xx, yy, np.sqrt(mahal_emp_cov), cmap=plt.cm.PuBu_r, linestyles="dashed"
)
# 计算基于MCD的马氏距离
mahal_robust_cov = robust_cov.mahalanobis(zz)
mahal_robust_cov = mahal_robust_cov.reshape(xx.shape)
robust_contour = ax.contour(
    xx, yy, np.sqrt(mahal_robust_cov), cmap=plt.cm.YlOrBr_r, linestyles="dotted"
)

# Add legend
ax.legend(
    [
        mlines.Line2D([], [], color="tab:blue", linestyle="dashed"),
        mlines.Line2D([], [], color="tab:orange", linestyle="dotted"),
        inlier_plot,
        outlier_plot,
    ],
    ["MLE dist", "MCD dist", "inliers", "outliers"],
    loc="upper right",
    borderaxespad=0,
)

plt.show()

Mahalanobis distances of a contaminated data set

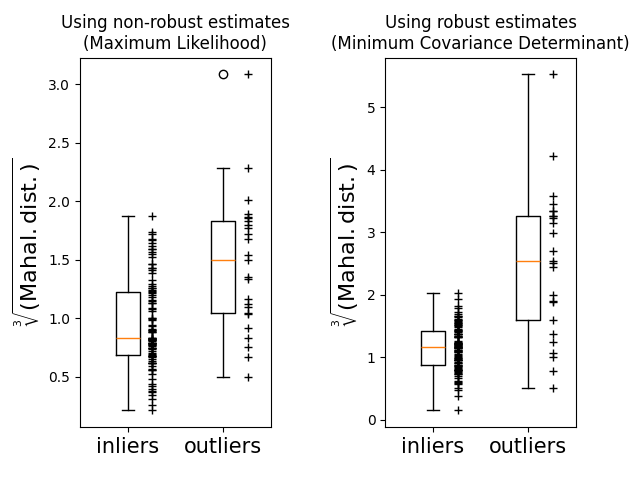
最后，我们强调了基于MCD的马氏距离区分异常值的能力。我们取马氏距离的立方根，得到近似正态分布（如Wilson和Hilferty [2]_所建议的），然后用箱线图绘制内点和异常点样本的值。对于基于稳健MCD的马氏距离，异常点样本的分布与内点样本的分布更加分离。

fig, (ax1, ax2) = plt.subplots(1, 2)
plt.subplots_adjust(wspace=0.6)

# 计算样本的MLE马氏距离的立方根
emp_mahal = emp_cov.mahalanobis(X - np.mean(X, 0)) ** (0.33)
# Plot boxplots
ax1.boxplot([emp_mahal[:-n_outliers], emp_mahal[-n_outliers:]], widths=0.25)
# Plot individual samples
ax1.plot(
    np.full(n_samples - n_outliers, 1.26),
    emp_mahal[:-n_outliers],
    "+k",
    markeredgewidth=1,
)
ax1.plot(np.full(n_outliers, 2.26), emp_mahal[-n_outliers:], "+k", markeredgewidth=1)
ax1.axes.set_xticklabels(("inliers", "outliers"), size=15)
ax1.set_ylabel(r"$\sqrt[3]{\rm{(Mahal. dist.)}}$", size=16)
ax1.set_title("Using non-robust estimates\n(Maximum Likelihood)")

# 计算样本的MCD马氏距离的立方根
robust_mahal = robust_cov.mahalanobis(X - robust_cov.location_) ** (0.33)
# Plot boxplots
ax2.boxplot([robust_mahal[:-n_outliers], robust_mahal[-n_outliers:]], widths=0.25)
# Plot individual samples
ax2.plot(
    np.full(n_samples - n_outliers, 1.26),
    robust_mahal[:-n_outliers],
    "+k",
    markeredgewidth=1,
)
ax2.plot(np.full(n_outliers, 2.26), robust_mahal[-n_outliers:], "+k", markeredgewidth=1)
ax2.axes.set_xticklabels(("inliers", "outliers"), size=15)
ax2.set_ylabel(r"$\sqrt[3]{\rm{(Mahal. dist.)}}$", size=16)
ax2.set_title("Using robust estimates\n(Minimum Covariance Determinant)")

plt.show()