Note
Go to the end to download the full example code. or to run this example in your browser via Binder
部分依赖图和个体条件期望图#
部分依赖图显示目标函数 [2] 与一组感兴趣特征之间的依赖关系,同时对所有其他特征(补充特征)的值进行边际化处理。由于人类感知的限制,感兴趣特征的集合大小必须很小(通常为一到两个),因此它们通常在最重要的特征中选择。
类似地,个体条件期望(ICE)图 [3] 显示目标函数与感兴趣特征之间的依赖关系。然而,与显示感兴趣特征平均效果的部分依赖图不同,ICE 图可视化每个样本的预测对特征的依赖关系,每个样本一条线。ICE 图仅支持一个感兴趣特征。
此示例展示了如何从训练在自行车共享数据集上的 MLPRegressor 和 HistGradientBoostingRegressor 中获取部分依赖图和 ICE 图。此示例的灵感来自 [1]。
自行车共享数据集预处理#
我们将使用共享单车数据集。目标是利用天气和季节数据以及日期时间信息来预测单车租赁数量。
from sklearn.datasets import fetch_openml
bikes = fetch_openml("Bike_Sharing_Demand", version=2, as_frame=True)
# 进行显式复制以避免 pandas 的 "SettingWithCopyWarning" 警告
X, y = bikes.data.copy(), bikes.target
# 我们只使用数据的一个子集来加快示例的速度。
X = X.iloc[::5, :]
y = y[::5]
特征“weather”有一个特点:类别“heavy_rain”是一个罕见类别。
X["weather"].value_counts()
weather
clear 2284
misty 904
rain 287
heavy_rain 1
Name: count, dtype: int64
由于这一罕见类别,我们将其合并为 "rain" 。
X["weather"] = (
X["weather"]
.astype(object)
.replace(to_replace="heavy_rain", value="rain")
.astype("category")
)
我们现在仔细看看 "year" 特征:
X["year"].value_counts()
year
1 1747
0 1729
Name: count, dtype: int64
我们可以看到我们有两年的数据。我们使用第一年的数据来训练模型,使用第二年的数据来测试模型。
mask_training = X["year"] == 0.0
X = X.drop(columns=["year"])
X_train, y_train = X[mask_training], y[mask_training]
X_test, y_test = X[~mask_training], y[~mask_training]
我们可以检查数据集信息,发现我们有异构数据类型。我们必须相应地预处理不同的列。
X_train.info()
<class 'pandas.core.frame.DataFrame'>
Index: 1729 entries, 0 to 8640
Data columns (total 11 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 season 1729 non-null category
1 month 1729 non-null int64
2 hour 1729 non-null int64
3 holiday 1729 non-null category
4 weekday 1729 non-null int64
5 workingday 1729 non-null category
6 weather 1729 non-null category
7 temp 1729 non-null float64
8 feel_temp 1729 non-null float64
9 humidity 1729 non-null float64
10 windspeed 1729 non-null float64
dtypes: category(4), float64(4), int64(3)
memory usage: 115.4 KB
根据前面的信息,我们将把 category 列视为名义分类特征。此外,我们还将把日期和时间信息视为分类特征。
我们手动定义包含数值和类别特征的列。
numerical_features = [
"temp",
"feel_temp",
"humidity",
"windspeed",
]
categorical_features = X_train.columns.drop(numerical_features)
在详细介绍不同机器学习管道的预处理之前,我们将尝试对数据集进行一些额外的直观分析,这将有助于理解模型的统计性能和部分依赖分析的结果。
我们通过按季节和年份对数据进行分组,绘制平均自行车租赁数量。
from itertools import product
import matplotlib.pyplot as plt
import numpy as np
days = ("Sun", "Mon", "Tue", "Wed", "Thu", "Fri", "Sat")
hours = tuple(range(24))
xticklabels = [f"{day}\n{hour}:00" for day, hour in product(days, hours)]
xtick_start, xtick_period = 6, 12
fig, axs = plt.subplots(nrows=2, figsize=(8, 6), sharey=True, sharex=True)
average_bike_rentals = bikes.frame.groupby(
["year", "season", "weekday", "hour"], observed=True
).mean(numeric_only=True)["count"]
for ax, (idx, df) in zip(axs, average_bike_rentals.groupby("year")):
df.groupby("season", observed=True).plot(ax=ax, legend=True)
# 装饰图表
ax.set_xticks(
np.linspace(
start=xtick_start,
stop=len(xticklabels),
num=len(xticklabels) // xtick_period,
)
)
ax.set_xticklabels(xticklabels[xtick_start::xtick_period])
ax.set_xlabel("")
ax.set_ylabel("Average number of bike rentals")
ax.set_title(
f"Bike rental for {'2010 (train set)' if idx == 0.0 else '2011 (test set)'}"
)
ax.set_ylim(0, 1_000)
ax.set_xlim(0, len(xticklabels))
ax.legend(loc=2)
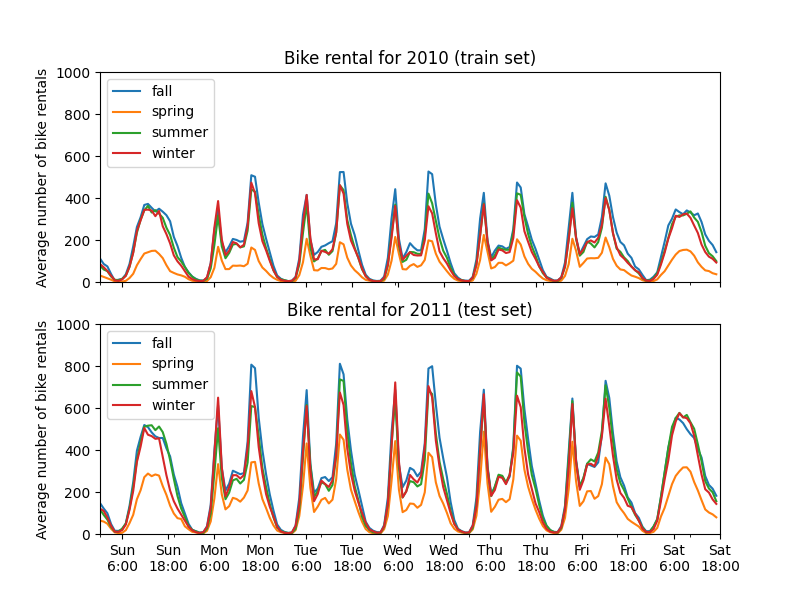
第一个显著的区别是测试集中的自行车租赁数量比训练集中更高。因此,得到一个低估自行车租赁数量的机器学习模型并不令人惊讶。我们还观察到,在春季,自行车租赁数量较低。此外,我们看到在工作日的早上6-7点和下午5-6点左右,自行车租赁数量有一些峰值。我们可以记住这些不同的见解,并利用它们来理解部分依赖图。
机器学习模型的预处理器#
由于我们后面会使用两个不同的模型,一个是 MLPRegressor ,另一个是 HistGradientBoostingRegressor ,因此我们为每个模型创建了两个不同的预处理器。
神经网络模型的预处理器#
我们将使用 QuantileTransformer 来缩放数值特征,并使用 OneHotEncoder 对类别特征进行编码。
from sklearn.compose import ColumnTransformer
from sklearn.preprocessing import OneHotEncoder, QuantileTransformer
mlp_preprocessor = ColumnTransformer(
transformers=[
("num", QuantileTransformer(n_quantiles=100), numerical_features),
("cat", OneHotEncoder(handle_unknown="ignore"), categorical_features),
]
)
mlp_preprocessor
梯度提升模型的预处理器#
对于梯度提升模型,我们保留数值特征不变,仅使用:class:~sklearn.preprocessing.OrdinalEncoder 对分类特征进行编码。
from sklearn.preprocessing import OrdinalEncoder
hgbdt_preprocessor = ColumnTransformer(
transformers=[
("cat", OrdinalEncoder(), categorical_features),
("num", "passthrough", numerical_features),
],
sparse_threshold=1,
verbose_feature_names_out=False,
).set_output(transform="pandas")
hgbdt_preprocessor
单变量部分依赖与不同模型的比较#
在本节中,我们将使用两种不同的机器学习模型计算一阶部分依赖:(i) 多层感知器和 (ii) 梯度提升模型。通过这两种模型,我们将展示如何计算和解释数值特征和分类特征的部分依赖图(PDP)以及个体条件期望(ICE)。
多层感知器#
让我们拟合一个 MLPRegressor 并计算单变量部分依赖图。
from time import time
from sklearn.neural_network import MLPRegressor
from sklearn.pipeline import make_pipeline
print("Training MLPRegressor...")
tic = time()
mlp_model = make_pipeline(
mlp_preprocessor,
MLPRegressor(
hidden_layer_sizes=(30, 15),
learning_rate_init=0.01,
early_stopping=True,
random_state=0,
),
)
mlp_model.fit(X_train, y_train)
print(f"done in {time() - tic:.3f}s")
print(f"Test R2 score: {mlp_model.score(X_test, y_test):.2f}")
Training MLPRegressor...
done in 0.251s
Test R2 score: 0.61
我们使用专门为神经网络创建的预处理器配置了一个管道,并调整了神经网络的规模和学习率,以在训练时间和测试集上的预测性能之间取得合理的折衷。
重要的是,这个表格数据集的特征具有非常不同的动态范围。神经网络往往对具有不同尺度的特征非常敏感,如果忘记对数值特征进行预处理,将导致模型表现非常差。
通过使用更大的神经网络,可以获得更高的预测性能,但训练成本也会显著增加。
请注意,在绘制部分依赖图之前,检查模型在测试集上的准确性非常重要,因为解释某个特征对预测函数的影响对于一个预测性能差的模型来说意义不大。在这方面,我们的MLP模型表现得相当不错。
我们将绘制平均部分依赖图。
import matplotlib.pyplot as plt
from sklearn.inspection import PartialDependenceDisplay
common_params = {
"subsample": 50,
"n_jobs": 2,
"grid_resolution": 20,
"random_state": 0,
}
print("Computing partial dependence plots...")
features_info = {
# 关注的特性
"features": ["temp", "humidity", "windspeed", "season", "weather", "hour"],
# 部分依赖图的类型
"kind": "average",
# 有关分类特征的信息
"categorical_features": categorical_features,
}
tic = time()
_, ax = plt.subplots(ncols=3, nrows=2, figsize=(9, 8), constrained_layout=True)
display = PartialDependenceDisplay.from_estimator(
mlp_model,
X_train,
**features_info,
ax=ax,
**common_params,
)
print(f"done in {time() - tic:.3f}s")
_ = display.figure_.suptitle(
(
"Partial dependence of the number of bike rentals\n"
"for the bike rental dataset with an MLPRegressor"
),
fontsize=16,
)
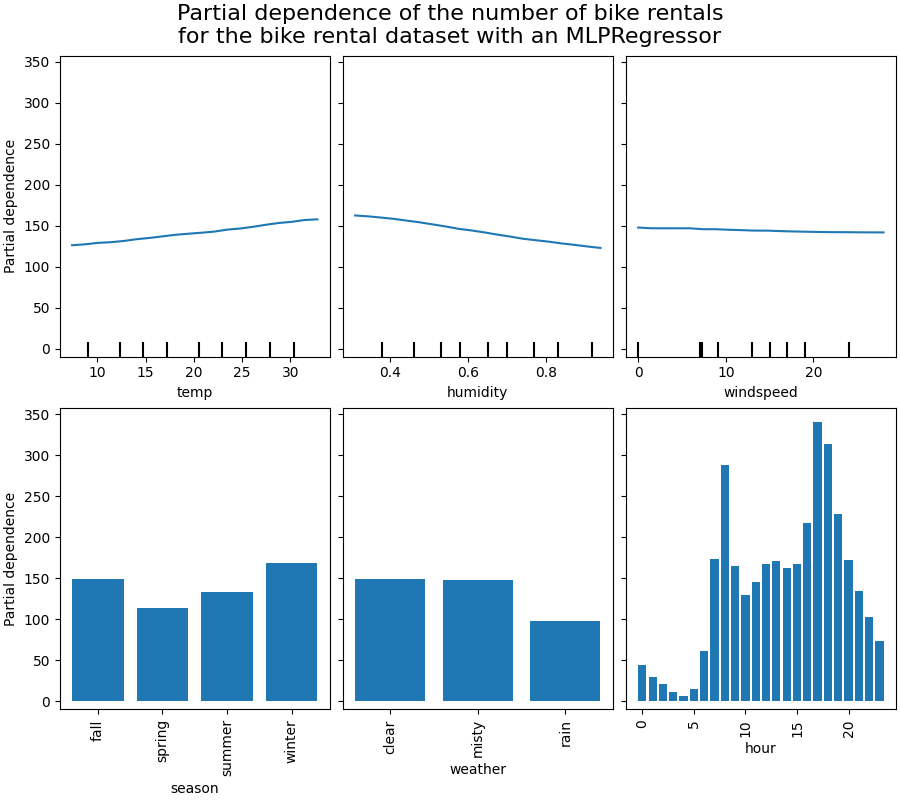
Computing partial dependence plots...
done in 0.342s
梯度提升#
现在让我们拟合一个 HistGradientBoostingRegressor 并计算相同特征的部分依赖性。我们还使用了为该模型创建的特定预处理器。
from sklearn.ensemble import HistGradientBoostingRegressor
print("Training HistGradientBoostingRegressor...")
tic = time()
hgbdt_model = make_pipeline(
hgbdt_preprocessor,
HistGradientBoostingRegressor(
categorical_features=categorical_features,
random_state=0,
max_iter=50,
),
)
hgbdt_model.fit(X_train, y_train)
print(f"done in {time() - tic:.3f}s")
print(f"Test R2 score: {hgbdt_model.score(X_test, y_test):.2f}")
Training HistGradientBoostingRegressor...
done in 0.157s
Test R2 score: 0.62
在这里,我们使用了梯度提升模型的默认超参数,没有进行任何预处理,因为基于树的模型对数值特征的单调变换具有天然的鲁棒性。
请注意,在这个表格数据集上,梯度提升机的训练速度比神经网络快得多,且更为准确。调节其超参数的成本也显著更低(默认参数往往效果很好,而神经网络通常不是这样)。
我们将绘制一些数值和类别特征的部分依赖图。
print("Computing partial dependence plots...")
tic = time()
_, ax = plt.subplots(ncols=3, nrows=2, figsize=(9, 8), constrained_layout=True)
display = PartialDependenceDisplay.from_estimator(
hgbdt_model,
X_train,
**features_info,
ax=ax,
**common_params,
)
print(f"done in {time() - tic:.3f}s")
_ = display.figure_.suptitle(
(
"Partial dependence of the number of bike rentals\n"
"for the bike rental dataset with a gradient boosting"
),
fontsize=16,
)
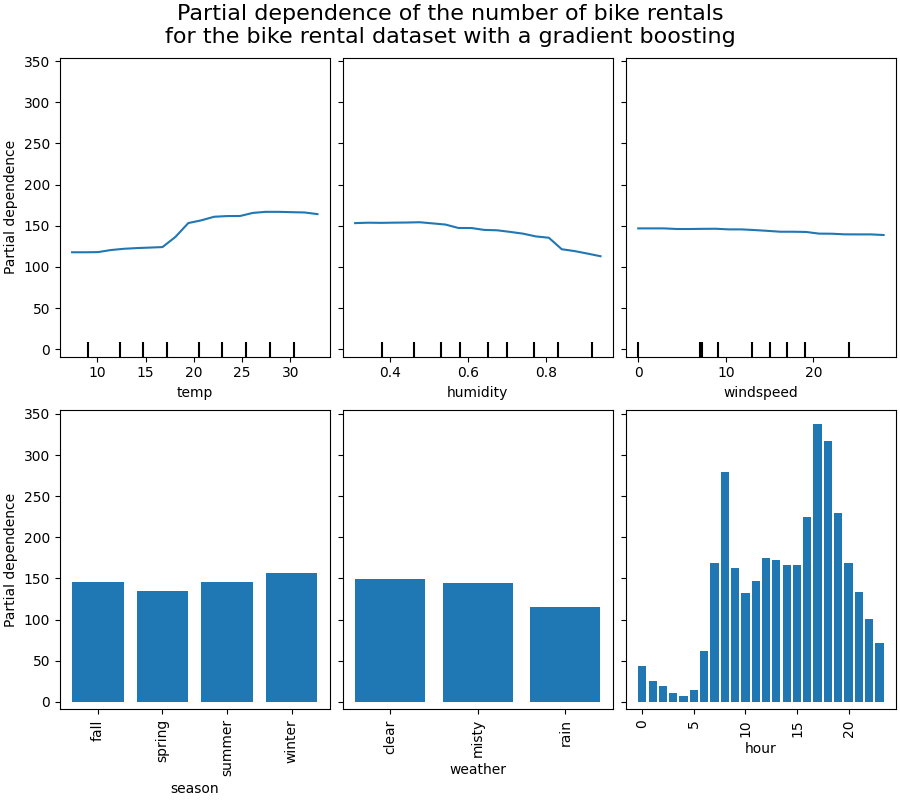
Computing partial dependence plots...
done in 0.574s
图表分析#
我们将首先查看数值特征的部分依赖图(PDP)。对于两个模型,温度的PDP的一般趋势是自行车租赁数量随着温度的升高而增加。我们可以对湿度特征进行类似的分析,但趋势相反。湿度增加时,自行车租赁数量减少。最后,我们看到风速特征也有相同的趋势。对于两个模型,风速增加时,自行车租赁数量减少。我们还观察到:class:~sklearn.neural_network.MLPRegressor 的预测比:class:~sklearn.ensemble.HistGradientBoostingRegressor 更平滑。
现在,我们将查看分类特征的部分依赖图。
我们观察到春季是季节特征中最低的。对于天气特征,雨天类别是最低的。关于小时特征,我们看到在早上7点和下午6点左右有两个高峰。这些发现与我们之前对数据集的观察一致。
然而,值得注意的是,如果特征是相关的,我们可能会创建潜在的无意义的合成样本。
ICE 与 PDP#
PDP 是特征边际效应的平均值。我们对提供的样本集的所有样本的响应进行了平均。因此,一些效应可能会被隐藏。在这种情况下,可以绘制每个个体的响应。这种表示称为个体效应图(ICE)。在下图中,我们绘制了温度和湿度特征的 50 个随机选择的 ICE。
print("Computing partial dependence plots and individual conditional expectation...")
tic = time()
_, ax = plt.subplots(ncols=2, figsize=(6, 4), sharey=True, constrained_layout=True)
features_info = {
"features": ["temp", "humidity"],
"kind": "both",
"centered": True,
}
display = PartialDependenceDisplay.from_estimator(
hgbdt_model,
X_train,
**features_info,
ax=ax,
**common_params,
)
print(f"done in {time() - tic:.3f}s")
_ = display.figure_.suptitle("ICE and PDP representations", fontsize=16)
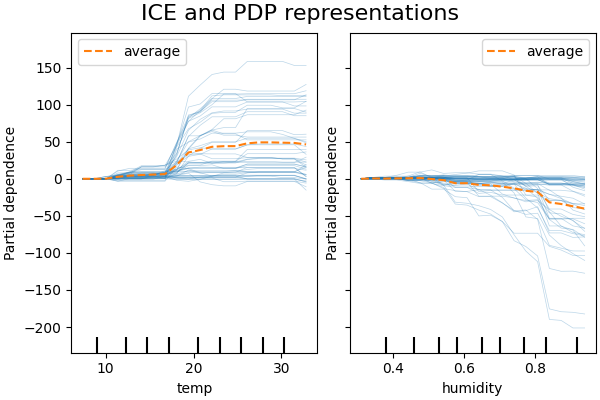
Computing partial dependence plots and individual conditional expectation...
done in 0.258s
我们看到温度特征的ICE为我们提供了一些额外的信息:一些ICE线是平坦的,而另一些则显示出温度高于35摄氏度时依赖性的下降。我们在湿度特征中观察到类似的模式:一些ICE线在湿度高于80%时显示出急剧下降。
并非所有的ICE线都是平行的,这表明模型发现了特征之间的交互作用。我们可以通过使用参数 interaction_cst 来约束梯度提升模型不使用任何特征之间的交互作用,从而重复该实验:
from sklearn.base import clone
interaction_cst = [[i] for i in range(X_train.shape[1])]
hgbdt_model_without_interactions = (
clone(hgbdt_model)
.set_params(histgradientboostingregressor__interaction_cst=interaction_cst)
.fit(X_train, y_train)
)
print(f"Test R2 score: {hgbdt_model_without_interactions.score(X_test, y_test):.2f}")
Test R2 score: 0.38
_, ax = plt.subplots(ncols=2, figsize=(6, 4), sharey=True, constrained_layout=True)
features_info["centered"] = False
display = PartialDependenceDisplay.from_estimator(
hgbdt_model_without_interactions,
X_train,
**features_info,
ax=ax,
**common_params,
)
_ = display.figure_.suptitle("ICE and PDP representations", fontsize=16)
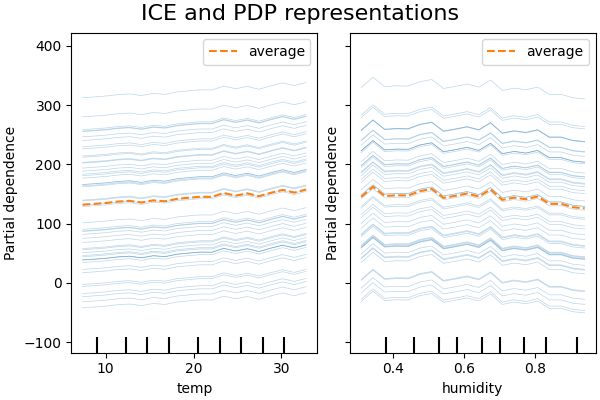
2D 交互图#
PDPs 具有两个感兴趣的特征,使我们能够可视化它们之间的交互。然而,ICEs 无法以简单的方式绘制和解释。我们将展示在 from_estimator 中可用的表示形式,即二维热图。
print("Computing partial dependence plots...")
features_info = {
"features": ["temp", "humidity", ("temp", "humidity")],
"kind": "average",
}
_, ax = plt.subplots(ncols=3, figsize=(10, 4), constrained_layout=True)
tic = time()
display = PartialDependenceDisplay.from_estimator(
hgbdt_model,
X_train,
**features_info,
ax=ax,
**common_params,
)
print(f"done in {time() - tic:.3f}s")
_ = display.figure_.suptitle(
"1-way vs 2-way of numerical PDP using gradient boosting", fontsize=16
)
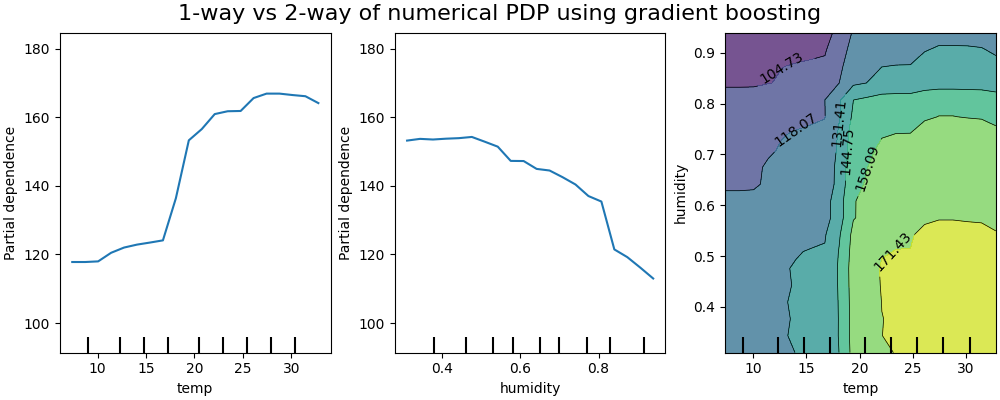
Computing partial dependence plots...
done in 4.206s
双向部分依赖图显示了自行车租赁数量对温度和湿度联合值的依赖关系。 我们清楚地看到这两个特征之间的相互作用。当温度高于20摄氏度时,湿度对自行车租赁数量的影响似乎独立于温度。
另一方面,当温度低于20摄氏度时,温度和湿度都会持续影响自行车租赁的数量。
此外,20摄氏度阈值的影响脊的斜率非常依赖于湿度水平:在干燥条件下,脊是陡峭的,但在湿度超过70%的潮湿条件下则要平缓得多。
我们现在将这些结果与为模型计算的相同图进行对比,该模型被限制为学习不依赖于此类非线性特征交互的预测函数。
print("Computing partial dependence plots...")
features_info = {
"features": ["temp", "humidity", ("temp", "humidity")],
"kind": "average",
}
_, ax = plt.subplots(ncols=3, figsize=(10, 4), constrained_layout=True)
tic = time()
display = PartialDependenceDisplay.from_estimator(
hgbdt_model_without_interactions,
X_train,
**features_info,
ax=ax,
**common_params,
)
print(f"done in {time() - tic:.3f}s")
_ = display.figure_.suptitle(
"1-way vs 2-way of numerical PDP using gradient boosting", fontsize=16
)
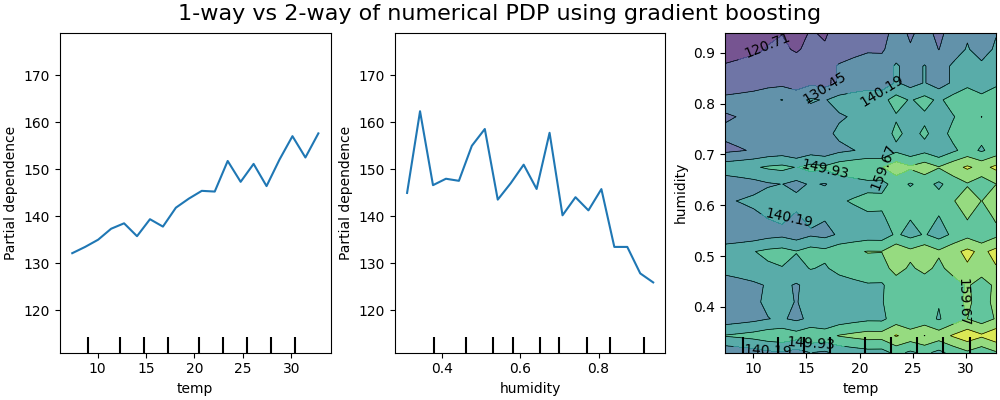
Computing partial dependence plots...
done in 4.455s
该模型在不考虑特征交互的情况下生成的一维部分依赖图显示了每个特征的局部峰值,特别是在“湿度”特征上。这些峰值可能反映了模型试图通过对特定训练点的过拟合来弥补被禁止的交互,从而导致模型表现退化。注意,该模型在测试集上的预测性能明显比原始的、无约束的模型差。
还请注意,这些图上可见的局部尖峰数量取决于PD图本身的网格分辨率参数。
那些局部尖峰导致了一个噪声栅格化的二维PD图。由于湿度特征中的高频振荡,很难判断这些特征之间是否没有交互作用。然而,可以清楚地看到,当温度越过20度边界时观察到的简单交互效应在这个模型中不再可见。
类别特征之间的部分依赖将提供一个离散表示,可以显示为热图。例如,季节、天气和目标之间的交互如下:
print("Computing partial dependence plots...")
features_info = {
"features": ["season", "weather", ("season", "weather")],
"kind": "average",
"categorical_features": categorical_features,
}
_, ax = plt.subplots(ncols=3, figsize=(14, 6), constrained_layout=True)
tic = time()
display = PartialDependenceDisplay.from_estimator(
hgbdt_model,
X_train,
**features_info,
ax=ax,
**common_params,
)
print(f"done in {time() - tic:.3f}s")
_ = display.figure_.suptitle(
"1-way vs 2-way PDP of categorical features using gradient boosting", fontsize=16
)
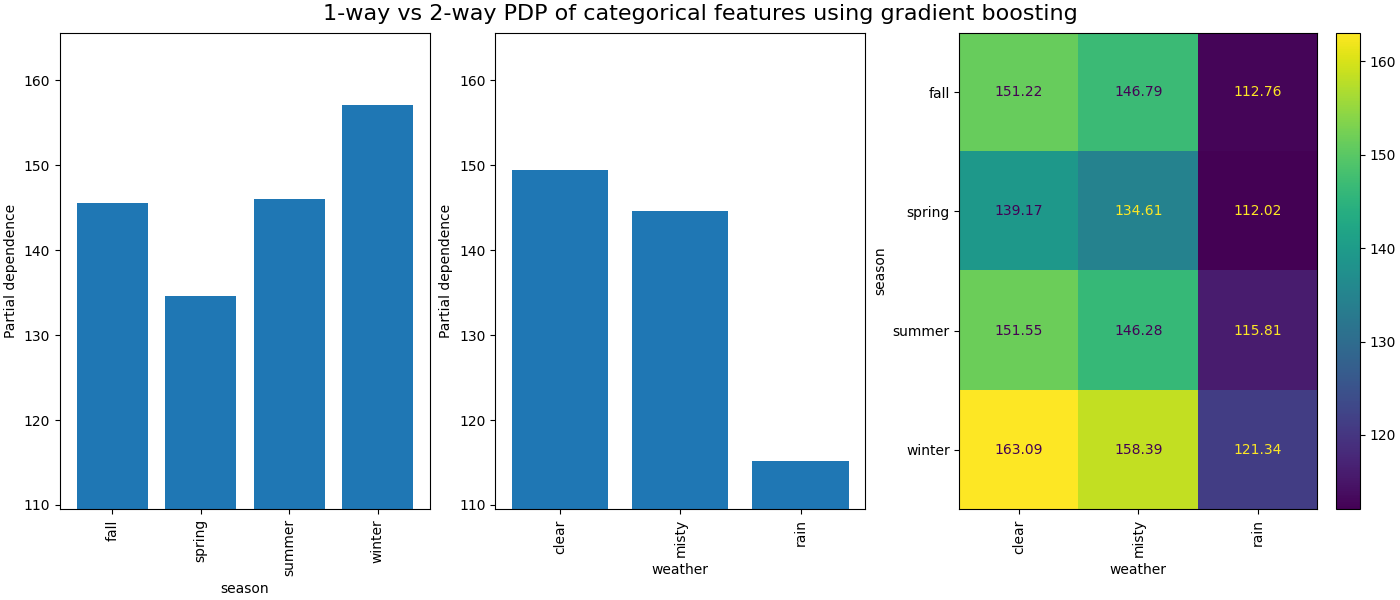
Computing partial dependence plots...
done in 0.234s
3D 表示#
让我们为这两个特征的交互作用绘制相同的部分依赖图,这次使用三维图。 未使用但必需的导入,用于在matplotlib < 3.2中进行3D投影。
import mpl_toolkits.mplot3d # noqa: F401
import numpy as np
from sklearn.inspection import partial_dependence
fig = plt.figure(figsize=(5.5, 5))
features = ("temp", "humidity")
pdp = partial_dependence(
hgbdt_model, X_train, features=features, kind="average", grid_resolution=10
)
XX, YY = np.meshgrid(pdp["grid_values"][0], pdp["grid_values"][1])
Z = pdp.average[0].T
ax = fig.add_subplot(projection="3d")
fig.add_axes(ax)
surf = ax.plot_surface(XX, YY, Z, rstride=1, cstride=1, cmap=plt.cm.BuPu, edgecolor="k")
ax.set_xlabel(features[0])
ax.set_ylabel(features[1])
fig.suptitle(
"PD of number of bike rentals on\nthe temperature and humidity GBDT model",
fontsize=16,
)
# 漂亮的初始化视图
ax.view_init(elev=22, azim=122)
clb = plt.colorbar(surf, pad=0.08, shrink=0.6, aspect=10)
clb.ax.set_title("Partial\ndependence")
plt.show()
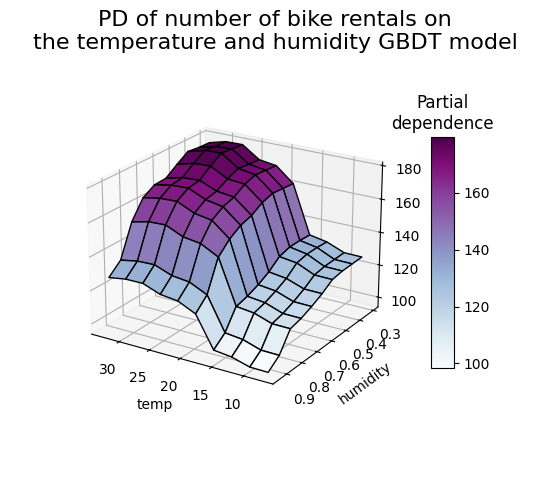
Total running time of the script: (0 minutes 13.415 seconds)
Related examples