Note
Go to the end to download the full example code. or to run this example in your browser via Binder
Lasso模型选择:AIC-BIC / 交叉验证#
本示例重点介绍Lasso模型的模型选择,Lasso模型是带有L1惩罚的线性回归模型。
实际上,有几种策略可以用来选择正则化参数的值:通过交叉验证或使用信息准则,即AIC或BIC。
在下文中,我们将详细讨论不同的策略。
# 作者:scikit-learn 开发者
# SPDX-License-Identifier: BSD-3-Clause
数据集#
在这个例子中,我们将使用糖尿病数据集。
from sklearn.datasets import load_diabetes
X, y = load_diabetes(return_X_y=True, as_frame=True)
X.head()
此外,我们在原始数据中添加了一些随机特征,以更好地说明Lasso模型执行的特征选择。
import numpy as np
import pandas as pd
rng = np.random.RandomState(42)
n_random_features = 14
X_random = pd.DataFrame(
rng.randn(X.shape[0], n_random_features),
columns=[f"random_{i:02d}" for i in range(n_random_features)],
)
X = pd.concat([X, X_random], axis=1)
# 仅显示部分列
X[X.columns[::3]].head()
通过信息准则选择Lasso#
LassoLarsIC 提供了一种Lasso估计器,
该估计器使用赤池信息准则(AIC)或贝叶斯信息准则(BIC)来选择正则化参数alpha的最优值。
在拟合模型之前,我们将使用:class:~sklearn.preprocessing.StandardScaler 对数据进行标准化。此外,我们将测量拟合和调整超参数alpha的时间,以便与交叉验证策略进行比较。
我们将首先使用AIC准则拟合一个Lasso模型。
import time
from sklearn.linear_model import LassoLarsIC
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
start_time = time.time()
lasso_lars_ic = make_pipeline(StandardScaler(), LassoLarsIC(criterion="aic")).fit(X, y)
fit_time = time.time() - start_time
我们存储在 fit 过程中使用的每个 alpha 值对应的 AIC 指标。
results = pd.DataFrame(
{
"alphas": lasso_lars_ic[-1].alphas_,
"AIC criterion": lasso_lars_ic[-1].criterion_,
}
).set_index("alphas")
alpha_aic = lasso_lars_ic[-1].alpha_
现在,我们使用BIC准则进行相同的分析。
lasso_lars_ic.set_params(lassolarsic__criterion="bic").fit(X, y)
results["BIC criterion"] = lasso_lars_ic[-1].criterion_
alpha_bic = lasso_lars_ic[-1].alpha_
我们可以检查哪个 alpha 值导致最小的 AIC 和 BIC。
def highlight_min(x):
x_min = x.min()
return ["font-weight: bold" if v == x_min else "" for v in x]
results.style.apply(highlight_min)
最终,我们可以绘制不同 alpha 值的 AIC 和 BIC 值。图中的垂直线对应于为每个准则选择的 alpha。所选的 alpha 对应于 AIC 或 BIC 准则的最小值。
ax = results.plot()
ax.vlines(
alpha_aic,
results["AIC criterion"].min(),
results["AIC criterion"].max(),
label="alpha: AIC estimate",
linestyles="--",
color="tab:blue",
)
ax.vlines(
alpha_bic,
results["BIC criterion"].min(),
results["BIC criterion"].max(),
label="alpha: BIC estimate",
linestyle="--",
color="tab:orange",
)
ax.set_xlabel(r"$\alpha$")
ax.set_ylabel("criterion")
ax.set_xscale("log")
ax.legend()
_ = ax.set_title(
f"Information-criterion for model selection (training time {fit_time:.2f}s)"
)
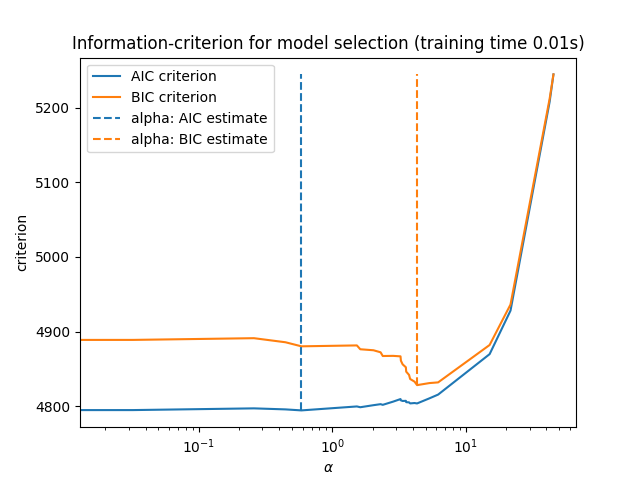
使用信息准则进行模型选择非常快速。它依赖于在提供给 fit 的样本集上计算准则。两个准则都基于训练集误差估计模型的泛化误差,并对这种过于乐观的误差进行惩罚。然而,这种惩罚依赖于自由度和噪声方差的适当估计。两者都是针对大样本(渐近结果)推导的,并假设模型是正确的,即数据实际上是由该模型生成的。
这些模型在问题条件不佳时(特征多于样本)也往往会失效。这时需要提供噪声方差的估计。
通过交叉验证选择Lasso#
Lasso估计器可以通过不同的求解器实现:坐标下降和最小角回归。它们在执行速度和数值误差来源方面有所不同。
在 scikit-learn 中,有两种带有集成交叉验证的估计器可用:LassoCV 和 LassoLarsCV ,它们分别使用坐标下降和最小角回归来解决问题。
在本节的剩余部分,我们将介绍这两种方法。对于这两种算法,我们将使用20折交叉验证策略。
通过坐标下降法进行Lasso回归#
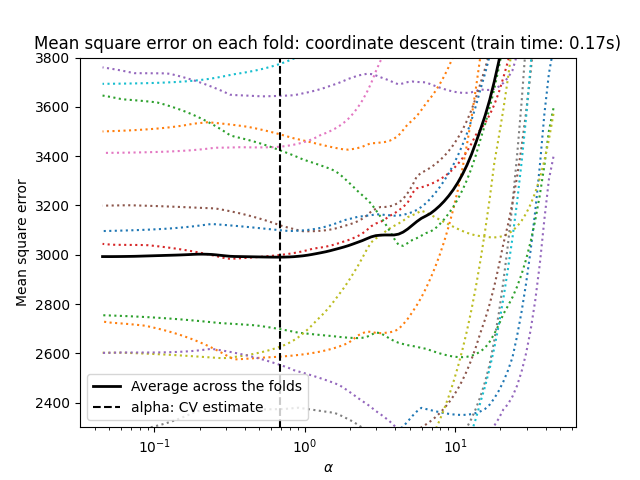
让我们开始使用 LassoCV 进行超参数调优。
from sklearn.linear_model import LassoCV
start_time = time.time()
model = make_pipeline(StandardScaler(), LassoCV(cv=20)).fit(X, y)
fit_time = time.time() - start_time
import matplotlib.pyplot as plt
ymin, ymax = 2300, 3800
lasso = model[-1]
plt.semilogx(lasso.alphas_, lasso.mse_path_, linestyle=":")
plt.plot(
lasso.alphas_,
lasso.mse_path_.mean(axis=-1),
color="black",
label="Average across the folds",
linewidth=2,
)
plt.axvline(lasso.alpha_, linestyle="--", color="black", label="alpha: CV estimate")
plt.ylim(ymin, ymax)
plt.xlabel(r"$\alpha$")
plt.ylabel("Mean square error")
plt.legend()
_ = plt.title(
f"Mean square error on each fold: coordinate descent (train time: {fit_time:.2f}s)"
)
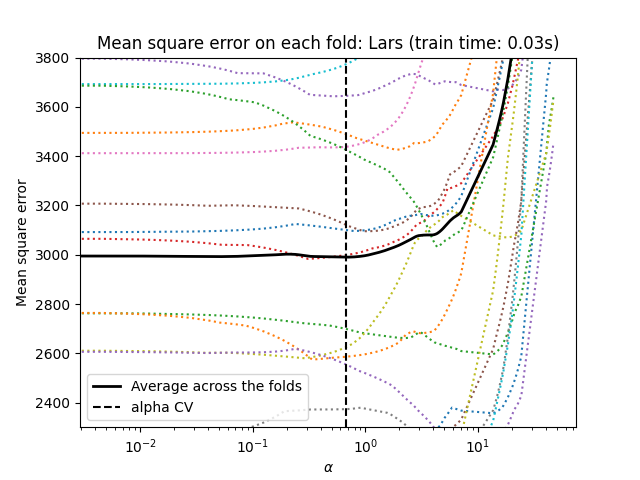
通过最小角回归进行套索回归#
让我们开始使用 LassoLarsCV 进行超参数调优。
from sklearn.linear_model import LassoLarsCV
start_time = time.time()
model = make_pipeline(StandardScaler(), LassoLarsCV(cv=20)).fit(X, y)
fit_time = time.time() - start_time
lasso = model[-1]
plt.semilogx(lasso.cv_alphas_, lasso.mse_path_, ":")
plt.semilogx(
lasso.cv_alphas_,
lasso.mse_path_.mean(axis=-1),
color="black",
label="Average across the folds",
linewidth=2,
)
plt.axvline(lasso.alpha_, linestyle="--", color="black", label="alpha CV")
plt.ylim(ymin, ymax)
plt.xlabel(r"$\alpha$")
plt.ylabel("Mean square error")
plt.legend()
_ = plt.title(f"Mean square error on each fold: Lars (train time: {fit_time:.2f}s)")
交叉验证方法总结#
两种算法给出的结果大致相同。
Lars 仅在路径中的每个拐点计算一个解路径。因此,当拐点较少时(例如特征或样本较少的情况),它非常高效。此外,它能够在不设置任何超参数的情况下计算完整路径。相反,坐标下降算法在预先指定的网格上计算路径点(此处我们使用默认值)。因此,如果网格点的数量小于路径中的拐点数量,它会更高效。如果特征数量非常大,并且每个交叉验证折叠中有足够的样本被选择,这种策略可能会很有趣。在数值误差方面,对于高度相关的变量,Lars 会积累更多的误差,而坐标下降算法只会在网格上采样路径。
请注意,alpha 的最优值在每个折叠中是如何变化的。这说明了在尝试评估一种通过交叉验证选择参数的方法的性能时,嵌套交叉验证是一个好的策略:这种参数选择可能并不适合仅在未见过的测试集上进行最终评估。
结论#
在本教程中,我们介绍了两种选择最佳超参数 alpha 的方法:一种策略仅使用训练集和一些信息准则来找到 alpha 的最优值,另一种策略基于交叉验证。
在这个例子中,两种方法的效果相似。样本内超参数选择在计算性能方面甚至显示了其有效性。然而,它只能在样本数量相对于特征数量足够大的情况下使用。
这就是为什么通过交叉验证进行超参数优化是一种安全策略:它在不同的设置中都有效。
Total running time of the script: (0 minutes 0.458 seconds)
Related examples