Note

Go to the end to download the full example code. or to run this example in your browser via Binder

球面上的流形学习方法#

在球形数据集上应用不同的流形学习技术。在这里可以看到使用降维技术来获得关于流形学习方法的一些直觉。关于数据集，球体的两极和侧面的一条薄片被切掉了。这使得流形学习技术能够在将其投影到二维时“展开”它。

对于一个类似的示例，其中这些方法应用于 S 曲线数据集，请参见流形学习方法的比较

请注意，MDS 的目的是找到数据的低维表示（此处为二维），其中距离很好地尊重原始高维空间中的距离，不同于其他流形学习算法，它不寻求数据在低维空间中的各向同性表示。在这里，流形问题相当于表示地球的平面地图，如地图投影。

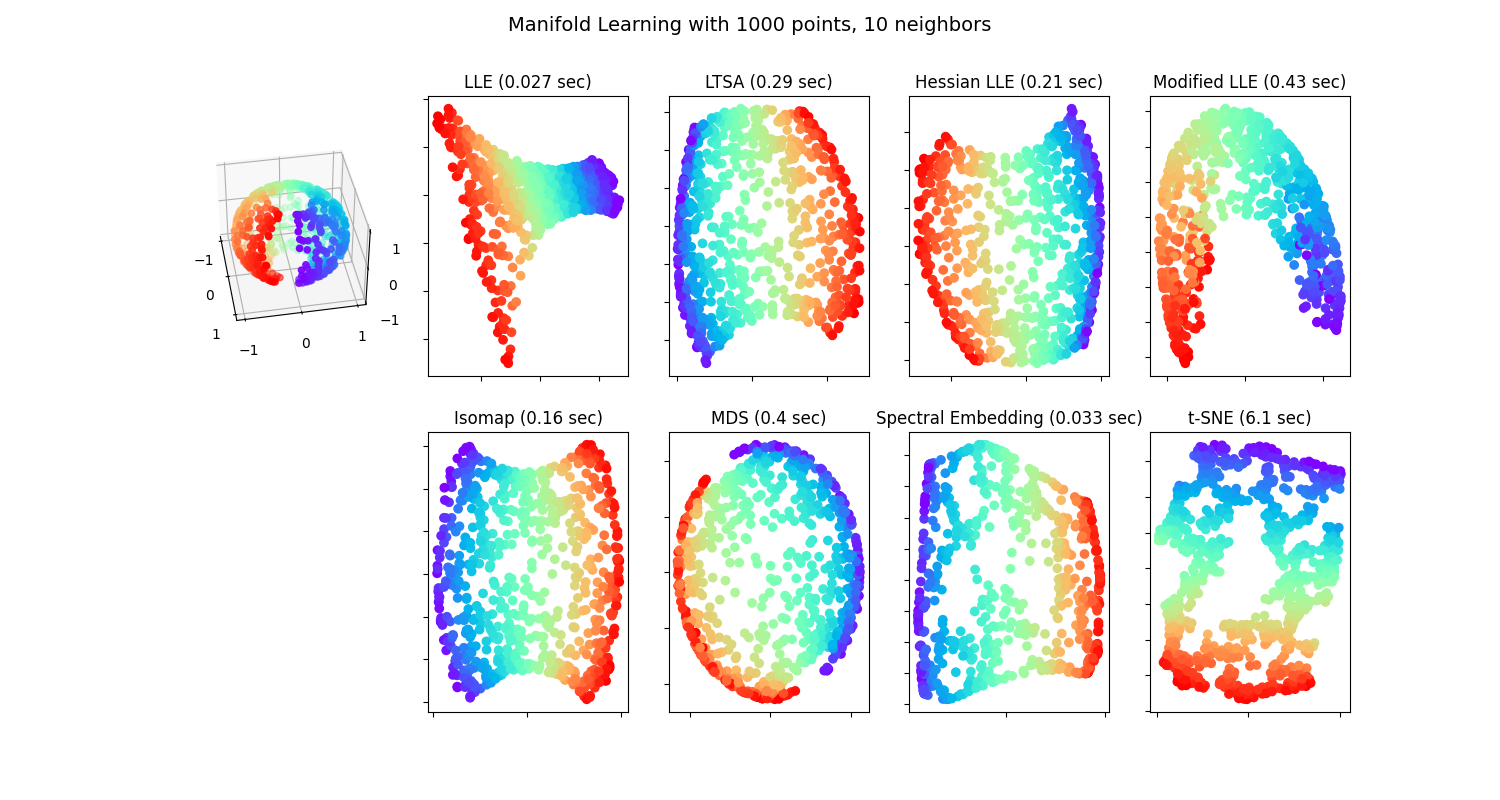
Manifold Learning with 1000 points, 10 neighbors, LLE (0.027 sec), LTSA (0.29 sec), Hessian LLE (0.21 sec), Modified LLE (0.43 sec), Isomap (0.16 sec), MDS (0.4 sec), Spectral Embedding (0.033 sec), t-SNE (6.1 sec)

standard: 0.027 sec
ltsa: 0.29 sec
hessian: 0.21 sec
modified: 0.43 sec
ISO: 0.16 sec
MDS: 0.4 sec
Spectral Embedding: 0.033 sec
t-SNE: 6.1 sec

# 作者：scikit-learn 开发者
# SPDX-License-Identifier：BSD-3-Clause

from time import time

import matplotlib.pyplot as plt

# 未使用但需要的导入，用于在 matplotlib < 3.2 中进行 3D 投影
import mpl_toolkits.mplot3d  # noqa: F401
import numpy as np
from matplotlib.ticker import NullFormatter

from sklearn import manifold
from sklearn.utils import check_random_state

# 流形学习的变量。
n_neighbors = 10
n_samples = 1000

# 创建我们的球体。
random_state = check_random_state(0)
p = random_state.rand(n_samples) * (2 * np.pi - 0.55)
t = random_state.rand(n_samples) * np.pi

# 将球体的两极切断。
indices = (t < (np.pi - (np.pi / 8))) & (t > ((np.pi / 8)))
colors = p[indices]
x, y, z = (
    np.sin(t[indices]) * np.cos(p[indices]),
    np.sin(t[indices]) * np.sin(p[indices]),
    np.cos(t[indices]),
)

# Plot our dataset.
fig = plt.figure(figsize=(15, 8))
plt.suptitle(
    "Manifold Learning with %i points, %i neighbors" % (1000, n_neighbors), fontsize=14
)

ax = fig.add_subplot(251, projection="3d")
ax.scatter(x, y, z, c=p[indices], cmap=plt.cm.rainbow)
ax.view_init(40, -10)

sphere_data = np.array([x, y, z]).T

# 执行局部线性嵌入流形学习
methods = ["standard", "ltsa", "hessian", "modified"]
labels = ["LLE", "LTSA", "Hessian LLE", "Modified LLE"]

for i, method in enumerate(methods):
    t0 = time()
    trans_data = (
        manifold.LocallyLinearEmbedding(
            n_neighbors=n_neighbors, n_components=2, method=method, random_state=42
        )
        .fit_transform(sphere_data)
        .T
    )
    t1 = time()
    print("%s: %.2g sec" % (methods[i], t1 - t0))

    ax = fig.add_subplot(252 + i)
    plt.scatter(trans_data[0], trans_data[1], c=colors, cmap=plt.cm.rainbow)
    plt.title("%s (%.2g sec)" % (labels[i], t1 - t0))
    ax.xaxis.set_major_formatter(NullFormatter())
    ax.yaxis.set_major_formatter(NullFormatter())
    plt.axis("tight")

# 执行 Isomap 流形学习。
t0 = time()
trans_data = (
    manifold.Isomap(n_neighbors=n_neighbors, n_components=2)
    .fit_transform(sphere_data)
    .T
)
t1 = time()
print("%s: %.2g sec" % ("ISO", t1 - t0))

ax = fig.add_subplot(257)
plt.scatter(trans_data[0], trans_data[1], c=colors, cmap=plt.cm.rainbow)
plt.title("%s (%.2g sec)" % ("Isomap", t1 - t0))
ax.xaxis.set_major_formatter(NullFormatter())
ax.yaxis.set_major_formatter(NullFormatter())
plt.axis("tight")

# 执行多维缩放。
t0 = time()
mds = manifold.MDS(2, max_iter=100, n_init=1, random_state=42)
trans_data = mds.fit_transform(sphere_data).T
t1 = time()
print("MDS: %.2g sec" % (t1 - t0))

ax = fig.add_subplot(258)
plt.scatter(trans_data[0], trans_data[1], c=colors, cmap=plt.cm.rainbow)
plt.title("MDS (%.2g sec)" % (t1 - t0))
ax.xaxis.set_major_formatter(NullFormatter())
ax.yaxis.set_major_formatter(NullFormatter())
plt.axis("tight")

# 执行谱嵌入。
t0 = time()
se = manifold.SpectralEmbedding(
    n_components=2, n_neighbors=n_neighbors, random_state=42
)
trans_data = se.fit_transform(sphere_data).T
t1 = time()
print("Spectral Embedding: %.2g sec" % (t1 - t0))

ax = fig.add_subplot(259)
plt.scatter(trans_data[0], trans_data[1], c=colors, cmap=plt.cm.rainbow)
plt.title("Spectral Embedding (%.2g sec)" % (t1 - t0))
ax.xaxis.set_major_formatter(NullFormatter())
ax.yaxis.set_major_formatter(NullFormatter())
plt.axis("tight")

# 执行t分布随机邻嵌入。
t0 = time()
tsne = manifold.TSNE(n_components=2, random_state=0)
trans_data = tsne.fit_transform(sphere_data).T
t1 = time()
print("t-SNE: %.2g sec" % (t1 - t0))

ax = fig.add_subplot(2, 5, 10)
plt.scatter(trans_data[0], trans_data[1], c=colors, cmap=plt.cm.rainbow)
plt.title("t-SNE (%.2g sec)" % (t1 - t0))
ax.xaxis.set_major_formatter(NullFormatter())
ax.yaxis.set_major_formatter(NullFormatter())
plt.axis("tight")

plt.show()