Note

Go to the end to download the full example code. or to run this example in your browser via Binder

L1-正则化路径的逻辑回归#

在从鸢尾花数据集中提取的二分类问题上训练带有L1惩罚项的逻辑回归模型。

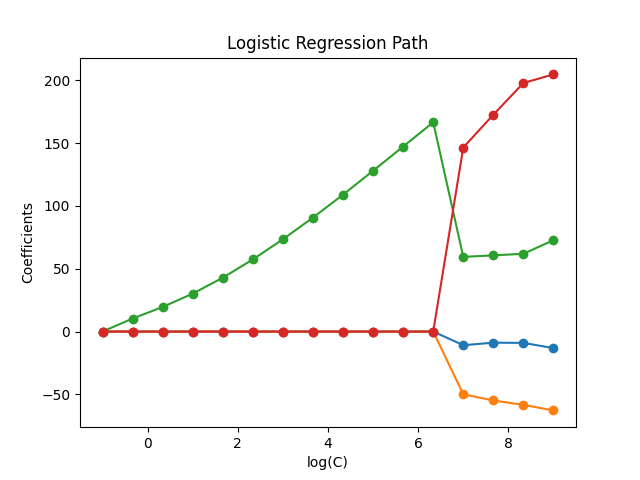
这些模型按从最强正则化到最弱正则化的顺序排列。收集并绘制模型的4个系数作为“正则化路径”：在图的左侧（强正则化器），所有系数都为0。当正则化逐渐减弱时，系数会一个接一个地变为非零值。

在这里我们选择liblinear求解器，因为它可以有效地优化带有非平滑、稀疏诱导的L1惩罚项的逻辑回归损失。

还要注意，我们设置了一个较低的容差值，以确保在收集系数之前模型已经收敛。

我们还使用了warm_start=True，这意味着模型的系数被重用以初始化下一个模型拟合，从而加快全路径的计算。

# 作者：scikit-learn 开发者
# SPDX-License-Identifier: BSD-3-Clause

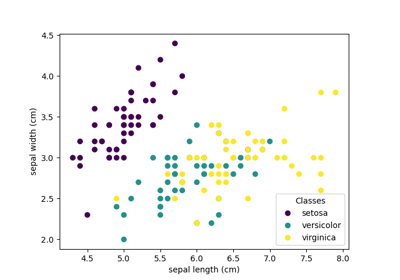
Load data#

from sklearn import datasets

iris = datasets.load_iris()
X = iris.data
y = iris.target

X = X[y != 2]
y = y[y != 2]

X /= X.max()  # Normalize X to speed-up convergence

计算正则化路径#

import numpy as np

from sklearn import linear_model
from sklearn.svm import l1_min_c

cs = l1_min_c(X, y, loss="log") * np.logspace(0, 10, 16)

clf = linear_model.LogisticRegression(
    penalty="l1",
    solver="liblinear",
    tol=1e-6,
    max_iter=int(1e6),
    warm_start=True,
    intercept_scaling=10000.0,
)
coefs_ = []
for c in cs:
    clf.set_params(C=c)
    clf.fit(X, y)
    coefs_.append(clf.coef_.ravel().copy())

coefs_ = np.array(coefs_)

绘制正则化路径#

import matplotlib.pyplot as plt

plt.plot(np.log10(cs), coefs_, marker="o")
ymin, ymax = plt.ylim()
plt.xlabel("log(C)")
plt.ylabel("Coefficients")
plt.title("Logistic Regression Path")
plt.axis("tight")
plt.show()