Note
Go to the end to download the full example code. or to run this example in your browser via Binder
3类分类的概率校准#
此示例说明了sigmoid 校准 如何改变3类分类问题的预测概率。图示为标准的2-单纯形,其中三个角对应三个类别。箭头从未经校准的分类器预测的概率向量指向同一分类器在保留验证集上进行sigmoid校准后的概率向量。颜色表示实例的真实类别(红色:类别1,绿色:类别2,蓝色:类别3)。
数据#
在下文中,我们生成了一个包含2000个样本、2个特征和3个目标类别的分类数据集。然后我们按如下方式拆分数据:
训练集:600个样本(用于训练分类器)
验证集:400个样本(用于校准预测概率)
测试集:1000个样本
请注意,我们还创建了 X_train_valid 和 y_train_valid ,它们包含了训练集和验证集的子集。当我们只想训练分类器而不校准预测概率时,会使用这些数据。
# 作者:scikit-learn 开发者
# SPDX-License-Identifier: BSD-3-Clause
import numpy as np
from sklearn.datasets import make_blobs
np.random.seed(0)
X, y = make_blobs(
n_samples=2000, n_features=2, centers=3, random_state=42, cluster_std=5.0
)
X_train, y_train = X[:600], y[:600]
X_valid, y_valid = X[600:1000], y[600:1000]
X_train_valid, y_train_valid = X[:1000], y[:1000]
X_test, y_test = X[1000:], y[1000:]
拟合与校准#
首先,我们将使用 25 个基估计器(树)的 RandomForestClassifier 在合并的训练和验证数据(1000 个样本)上进行训练。这是未经校准的分类器。
from sklearn.ensemble import RandomForestClassifier
clf = RandomForestClassifier(n_estimators=25)
clf.fit(X_train_valid, y_train_valid)
为了训练校准后的分类器,我们首先使用相同的:class:~sklearn.ensemble.RandomForestClassifier ,但仅使用训练数据子集(600个样本)进行训练,然后在一个两阶段的过程中使用验证数据子集(400个样本)并采用 method='sigmoid' 进行校准。
from sklearn.calibration import CalibratedClassifierCV
clf = RandomForestClassifier(n_estimators=25)
clf.fit(X_train, y_train)
cal_clf = CalibratedClassifierCV(clf, method="sigmoid", cv="prefit")
cal_clf.fit(X_valid, y_valid)
比较概率#
下面我们绘制了一个2-单纯形,并用箭头显示了测试样本预测概率的变化。
import matplotlib.pyplot as plt
plt.figure(figsize=(10, 10))
colors = ["r", "g", "b"]
clf_probs = clf.predict_proba(X_test)
cal_clf_probs = cal_clf.predict_proba(X_test)
# Plot arrows
for i in range(clf_probs.shape[0]):
plt.arrow(
clf_probs[i, 0],
clf_probs[i, 1],
cal_clf_probs[i, 0] - clf_probs[i, 0],
cal_clf_probs[i, 1] - clf_probs[i, 1],
color=colors[y_test[i]],
head_width=1e-2,
)
# 绘制完美预测,在每个顶点处
plt.plot([1.0], [0.0], "ro", ms=20, label="Class 1")
plt.plot([0.0], [1.0], "go", ms=20, label="Class 2")
plt.plot([0.0], [0.0], "bo", ms=20, label="Class 3")
# 绘制单位单纯形的边界
plt.plot([0.0, 1.0, 0.0, 0.0], [0.0, 0.0, 1.0, 0.0], "k", label="Simplex")
# 标注单纯形周围的6个点,以及单纯形内部的中点
plt.annotate(
r"($\frac{1}{3}$, $\frac{1}{3}$, $\frac{1}{3}$)",
xy=(1.0 / 3, 1.0 / 3),
xytext=(1.0 / 3, 0.23),
xycoords="data",
arrowprops=dict(facecolor="black", shrink=0.05),
horizontalalignment="center",
verticalalignment="center",
)
plt.plot([1.0 / 3], [1.0 / 3], "ko", ms=5)
plt.annotate(
r"($\frac{1}{2}$, $0$, $\frac{1}{2}$)",
xy=(0.5, 0.0),
xytext=(0.5, 0.1),
xycoords="data",
arrowprops=dict(facecolor="black", shrink=0.05),
horizontalalignment="center",
verticalalignment="center",
)
plt.annotate(
r"($0$, $\frac{1}{2}$, $\frac{1}{2}$)",
xy=(0.0, 0.5),
xytext=(0.1, 0.5),
xycoords="data",
arrowprops=dict(facecolor="black", shrink=0.05),
horizontalalignment="center",
verticalalignment="center",
)
plt.annotate(
r"($\frac{1}{2}$, $\frac{1}{2}$, $0$)",
xy=(0.5, 0.5),
xytext=(0.6, 0.6),
xycoords="data",
arrowprops=dict(facecolor="black", shrink=0.05),
horizontalalignment="center",
verticalalignment="center",
)
plt.annotate(
r"($0$, $0$, $1$)",
xy=(0, 0),
xytext=(0.1, 0.1),
xycoords="data",
arrowprops=dict(facecolor="black", shrink=0.05),
horizontalalignment="center",
verticalalignment="center",
)
plt.annotate(
r"($1$, $0$, $0$)",
xy=(1, 0),
xytext=(1, 0.1),
xycoords="data",
arrowprops=dict(facecolor="black", shrink=0.05),
horizontalalignment="center",
verticalalignment="center",
)
plt.annotate(
r"($0$, $1$, $0$)",
xy=(0, 1),
xytext=(0.1, 1),
xycoords="data",
arrowprops=dict(facecolor="black", shrink=0.05),
horizontalalignment="center",
verticalalignment="center",
)
# Add grid
plt.grid(False)
for x in [0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0]:
plt.plot([0, x], [x, 0], "k", alpha=0.2)
plt.plot([0, 0 + (1 - x) / 2], [x, x + (1 - x) / 2], "k", alpha=0.2)
plt.plot([x, x + (1 - x) / 2], [0, 0 + (1 - x) / 2], "k", alpha=0.2)
plt.title("Change of predicted probabilities on test samples after sigmoid calibration")
plt.xlabel("Probability class 1")
plt.ylabel("Probability class 2")
plt.xlim(-0.05, 1.05)
plt.ylim(-0.05, 1.05)
_ = plt.legend(loc="best")
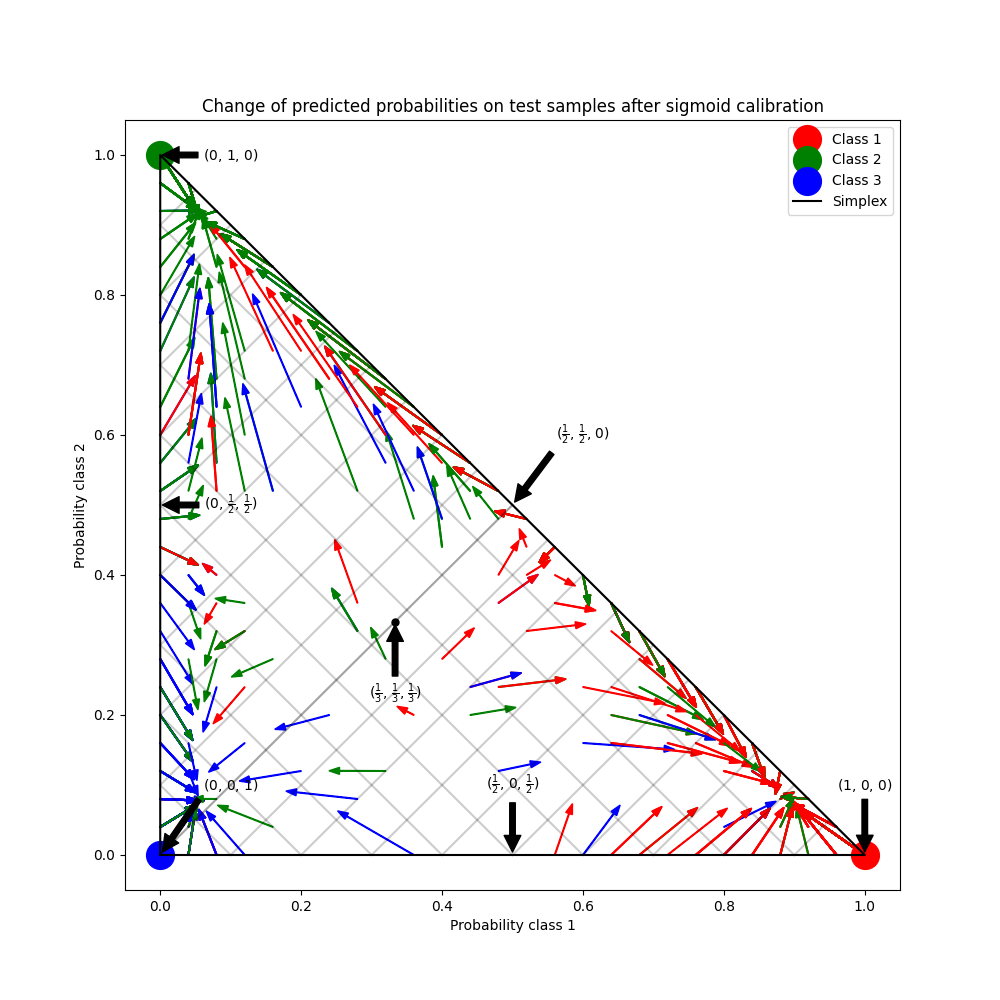
在上图中,单纯形的每个顶点代表一个完全预测的类别(例如,1, 0, 0)。单纯形内部的中点表示以相等概率预测三个类别(即,1/3, 1/3, 1/3)。每个箭头从未校准的概率开始,箭头尖端指向校准后的概率。箭头的颜色表示该测试样本的真实类别。
未经校准的分类器对其预测过于自信,并且会产生较大的 对数损失 。校准后的分类器由于两个因素会产生较低的 对数损失 。首先,注意上图中的箭头通常远离单纯形的边缘,即某一类的概率为0的地方。其次,大部分箭头指向真实类别,例如,绿色箭头(真实类别为“绿色”的样本)通常指向绿色顶点。这导致过于自信的0预测概率减少,同时正确类别的预测概率增加。因此,校准后的分类器会产生更准确的预测概率,从而导致较低的 对数损失 。
我们可以通过比较未校准和校准分类器在1000个测试样本预测上的:ref:对数损失 <log_loss> 来客观地展示这一点。请注意,另一种方法是增加:class:~sklearn.ensemble.RandomForestClassifier 的基估计器(树)的数量,这也会导致:ref:对数损失 <log_loss> 的类似减少。
Log-loss of
* uncalibrated classifier: 1.327
* calibrated classifier: 0.549
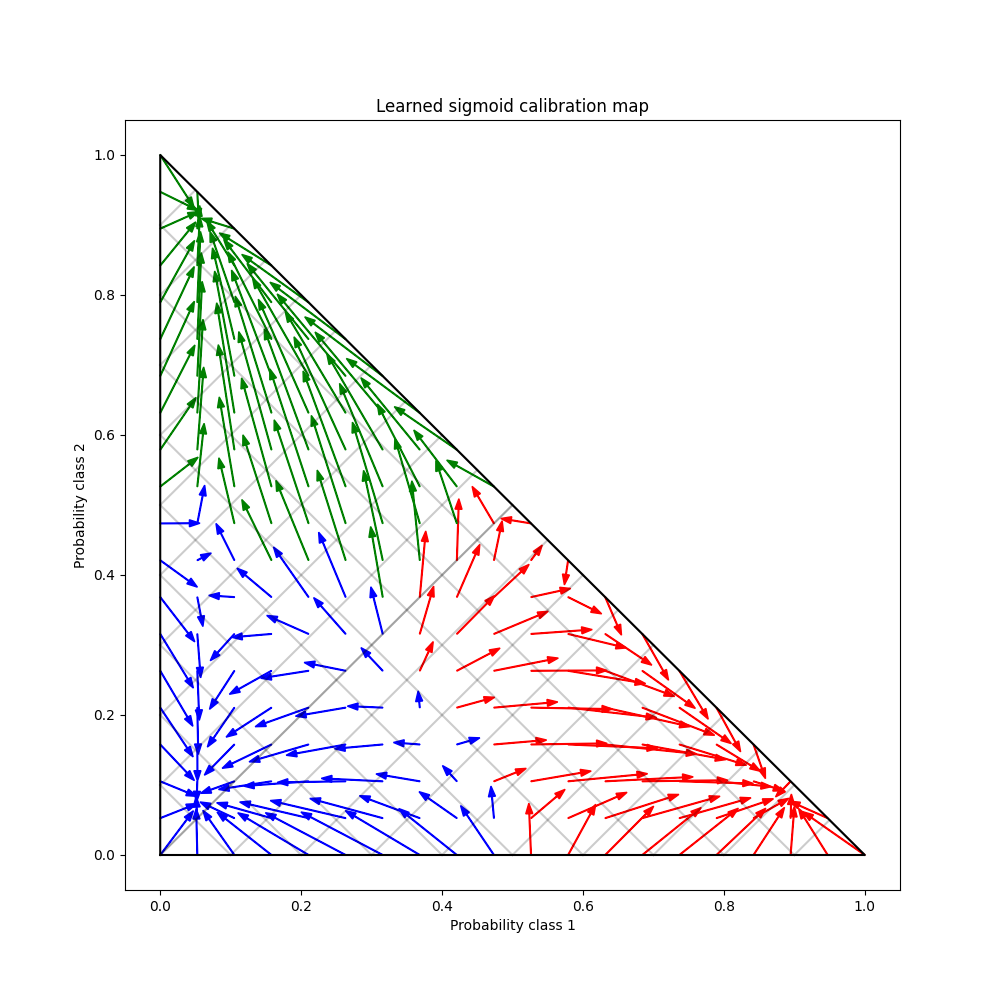
最终我们生成了一个在2-单纯形上的可能的未校准概率网格,计算相应的校准概率,并为每个概率绘制箭头。箭头根据最高的未校准概率进行着色。这展示了学习到的校准映射:
plt.figure(figsize=(10, 10))
# 生成概率值网格
p1d = np.linspace(0, 1, 20)
p0, p1 = np.meshgrid(p1d, p1d)
p2 = 1 - p0 - p1
p = np.c_[p0.ravel(), p1.ravel(), p2.ravel()]
p = p[p[:, 2] >= 0]
# 使用三个类别校准器来计算校准后的概率
calibrated_classifier = cal_clf.calibrated_classifiers_[0]
prediction = np.vstack(
[
calibrator.predict(this_p)
for calibrator, this_p in zip(calibrated_classifier.calibrators, p.T)
]
).T
# 重新归一化校准后的预测值,以确保它们保持在单纯形内。在多类问题中,CalibratedClassifierCV 的 predict 方法会在内部执行相同的重新归一化步骤。
prediction /= prediction.sum(axis=1)[:, None]
# 绘制校准器引起的预测概率变化
for i in range(prediction.shape[0]):
plt.arrow(
p[i, 0],
p[i, 1],
prediction[i, 0] - p[i, 0],
prediction[i, 1] - p[i, 1],
head_width=1e-2,
color=colors[np.argmax(p[i])],
)
# 绘制单位单纯形的边界
plt.plot([0.0, 1.0, 0.0, 0.0], [0.0, 0.0, 1.0, 0.0], "k", label="Simplex")
plt.grid(False)
for x in [0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0]:
plt.plot([0, x], [x, 0], "k", alpha=0.2)
plt.plot([0, 0 + (1 - x) / 2], [x, x + (1 - x) / 2], "k", alpha=0.2)
plt.plot([x, x + (1 - x) / 2], [0, 0 + (1 - x) / 2], "k", alpha=0.2)
plt.title("Learned sigmoid calibration map")
plt.xlabel("Probability class 1")
plt.ylabel("Probability class 2")
plt.xlim(-0.05, 1.05)
plt.ylim(-0.05, 1.05)
plt.show()
Total running time of the script: (0 minutes 0.719 seconds)
Related examples