3.4. 度量和评分：量化预测质量#

评估模型预测质量有三种不同的API：

最后， 虚拟估计器 对于随机预测的这些度量的基线值很有用。

See also

对于“成对”度量，在 样本 之间而不是估计器或预测之间，请参阅 成对度量、亲和力和核函数 部分。

scoring 参数：定义模型评估规则

使用工具（如 model_selection.GridSearchCV 和 model_selection.cross_val_score ）进行模型选择和评估时，可以使用 scoring 参数控制它们应用于评估估计器的度量标准。

3.4.1. 常见情况：预定义值#

对于最常见的情况，您可以使用 scoring 参数指定一个评分器对象；下表显示了所有可能的值。 所有评分器对象都遵循一个约定，即**更高的返回值优于更低的返回值**。因此，衡量模型与数据之间距离的指标，如 metrics.mean_squared_error ，可以通过 neg_mean_squared_error 返回该指标的负值。

使用示例：

>>> from sklearn import svm, datasets
>>> from sklearn.model_selection import cross_val_score
>>> X, y = datasets.load_iris(return_X_y=True)
>>> clf = svm.SVC(random_state=0)
>>> cross_val_score(clf, X, y, cv=5, scoring='recall_macro')
array([0.96..., 0.96..., 0.96..., 0.93..., 1.        ])

Note

如果传递了错误的评分名称，则会引发 InvalidParameterError 。 您可以通过调用 get_scorer_names 来检索所有可用评分器的名称。

3.4.2. 从指标函数定义您的评分策略#

以下指标函数未实现为命名评分器，有时是因为它们需要额外的参数，例如 fbeta_score 。 它们不能传递给 scoring 参数；相反，它们的可调用对象需要与用户设置的参数值一起传递给 make_scorer 。

一个典型的用例是使用库中现有指标函数的非默认参数值来包装该函数，例如 fbeta_score 函数的 beta 参数:

>>> from sklearn.metrics import fbeta_score, make_scorer
>>> ftwo_scorer = make_scorer(fbeta_score, beta=2)
>>> from sklearn.model_selection import GridSearchCV
>>> from sklearn.svm import LinearSVC
>>> grid = GridSearchCV(LinearSVC(), param_grid={'C': [1, 10]},
...                     scoring=ftwo_scorer, cv=5)

sklearn.metrics 模块还公开了一组简单的函数，用于测量给定真实值和预测值的预测误差：

  • 以 _score 结尾的函数返回一个值以最大化，值越高越好。

  • 以 _error 、 _loss 或 _deviance 结尾的函数返回一个值以最小化，值越低越好。当使用 make_scorer 将其转换为评分器对象时，将 greater_is_better 参数设置为 False （默认为 True ；请参阅下面的参数描述）。

#自定义评分器对象

第二个用例是使用 make_scorer 从简单的 Python 函数构建完全自定义的评分器对象，该函数可以接受多个参数：

  • 你想要使用的 Python 函数（例如下面的 my_custom_loss_func ）

  • Python 函数返回的是分数（ greater_is_better=True ，默认）还是损失（ greater_is_better=False ）。如果是损失，Python 函数的输出将由评分器对象取负，以符合交叉验证的约定，即评分器返回的值越高表示模型越好。

  • 仅适用于分类指标：您提供的Python函数是否需要连续的决策确定性。如果评分函数仅接受概率估计（例如:func:metrics.log_loss ），则需要设置参数 response_method ，因此在这种情况下 response_method="predict_proba" 。某些评分函数不一定需要概率估计，而是需要非阈值决策值（例如:func:metrics.roc_auc_score ）。在这种情况下，可以提供一个列表，例如 response_method=["decision_function", "predict_proba"] 。在这种情况下，评分器将按照列表中给出的顺序使用第一个可用方法来计算分数。

  • 任何其他参数，例如:func:f1_score 中的 beta 或 labels 。

以下是构建自定义评分器并使用 greater_is_better 参数的示例:

>>> import numpy as np
>>> def my_custom_loss_func(y_true, y_pred):
...     diff = np.abs(y_true - y_pred).max()
...     return np.log1p(diff)
...
>>> # score将否定my_custom_loss_func的返回值，
>>> # 即给定X和y的值，结果为np.log(2)，0.693。
>>> score = make_scorer(my_custom_loss_func, greater_is_better=False)
>>> X = [[1], [1]]
>>> y = [0, 1]
>>> from sklearn.dummy import DummyClassifier
>>> clf = DummyClassifier(strategy='most_frequent', random_state=0)
>>> clf = clf.fit(X, y)
>>> my_custom_loss_func(y, clf.predict(X))
0.69...
>>> score(clf, X, y)
-0.69...

3.4.3. 实现自己的评分对象#

您可以通过从头开始构建自己的评分对象，而无需使用:func:make_scorer 工厂，来生成更加灵活的模型评分器。

#如何从头开始构建评分器

对于一个可调用对象来说，要成为一个评分器，它需要满足以下两条规则所指定的协议：

  • 它可以使用参数 (estimator, X, y) 进行调用，其中 estimator 是应该被评估的模型， X 是验证数据，而 y 是 X 的基准真值目标（在监督学习情况下）或 None （在无监督学习情况下）。

  • 它返回一个浮点数，该数值量化了 estimator 在 X 上的预测质量，参照 y 。再次强调，按照惯例，数值越高表示越好，因此如果你的评分器返回的是损失值，该值应该被取反。

  • 高级：如果它需要传递额外的元数据，它应该暴露一个 get_metadata_routing 方法，返回请求的元数据。用户应该能够通过 set_score_request 方法设置请求的元数据。请参阅 用户指南 和 开发者指南 了解更多详情。

Note

在函数中使用自定义评分器且 n_jobs > 1 时

虽然在与调用函数一起定义自定义评分函数时，使用默认的 joblib 后端（loky）应该可以直接工作，但从另一个模块导入它将是一个更健壮的方法，并且独立于 joblib 后端工作。

例如，要在下面的示例中使用 n_jobs 大于 1， custom_scoring_function 函数保存在用户创建的模块（ custom_scorer_module.py ）中并导入:

>>> from custom_scorer_module import custom_scoring_function 
>>> cross_val_score(model,
...  X_train,
...  y_train,
...  scoring=make_scorer(custom_scoring_function, greater_is_better=False),
...  cv=5,
...  n_jobs=-1)

3.4.4. 使用多指标评估#

Scikit-learn 还允许在 GridSearchCV 、 RandomizedSearchCV 和 cross_validate 中评估多个指标。

有三种方法可以为 scoring 参数指定多个评分指标：

  • 作为字符串指标的可迭代对象::
    >>> scoring = ['accuracy', 'precision']
  • 作为映射评分器名称到评分函数的 dict ::
    >>> from sklearn.metrics import accuracy_score
>>> from sklearn.metrics import make_scorer
>>> scoring = {'accuracy': make_scorer(accuracy_score),
...            'prec': 'precision'}

    注意，字典的值可以是评分器函数或预定义的指标字符串之一。

  • 作为返回评分字典的可调用对象:

    >>> from sklearn.model_selection import cross_validate
>>> from sklearn.metrics import confusion_matrix
>>> # 一个示例的二分类数据集
>>> X, y = datasets.make_classification(n_classes=2, random_state=0)
>>> svm = LinearSVC(random_state=0)
>>> def confusion_matrix_scorer(clf, X, y):
...      y_pred = clf.predict(X)
...      cm = confusion_matrix(y, y_pred)
...      return {'tn': cm[0, 0], 'fp': cm[0, 1],
...              'fn': cm[1, 0], 'tp': cm[1, 1]}
>>> cv_results = cross_validate(svm, X, y, cv=5,
...                             scoring=confusion_matrix_scorer)
>>> # 获取测试集的真阳性分数
>>> print(cv_results['test_tp'])
[10  9  8  7  8]
>>> # 获取测试集的假阴性分数
>>> print(cv_results['test_fn'])
[0 1 2 3 2]

3.4.4.1. 分类指标#

sklearn.metrics 模块实现了多个用于衡量分类性能的损失、评分和实用函数。 某些指标可能需要正类的概率估计、置信值或二值决策值。 大多数实现允许每个样本通过 sample_weight 参数对总体得分提供加权贡献。

其中一些仅限于二分类情况：

precision_recall_curve(y_true[, y_score, ...])

计算不同概率阈值下的精确率-召回率对。

roc_curve(y_true, y_score, *[, pos_label, ...])

计算接收者操作特征（ROC）。

class_likelihood_ratios(y_true, y_pred, *[, ...])

计算二分类的正负似然比。

det_curve(y_true, y_score[, pos_label, ...])

计算不同概率阈值下的错误率。

其他一些也适用于多分类情况：

balanced_accuracy_score(y_true, y_pred, *[, ...])

计算平衡准确率。

cohen_kappa_score(y1, y2, *[, labels, ...])

计算Cohen's kappa：一种衡量标注者之间一致性的统计量。

confusion_matrix(y_true, y_pred, *[, ...])

计算混淆矩阵以评估分类的准确性。

hinge_loss(y_true, pred_decision, *[, ...])

平均铰链损失（非正则化）。

matthews_corrcoef(y_true, y_pred, *[, ...])

计算 Matthews 相关系数（MCC）。

roc_auc_score(y_true, y_score, *[, average, ...])

计算从预测分数得到的受试者工作特征曲线（ROC AUC）下的面积。

top_k_accuracy_score(y_true, y_score, *[, ...])

Top-k 准确率分类得分。

还有一些也适用于多标签情况：

accuracy_score(y_true, y_pred, *[, ...])

准确性分类得分。

classification_report(y_true, y_pred, *[, ...])

构建一个文本报告，展示主要的分类指标。

f1_score(y_true, y_pred, *[, labels, ...])

计算F1分数，也称为平衡F-分数或F-度量。

fbeta_score(y_true, y_pred, *, beta[, ...])

计算 F-beta 分数。

hamming_loss(y_true, y_pred, *[, sample_weight])

计算平均汉明损失。

jaccard_score(y_true, y_pred, *[, labels, ...])

Jaccard相似系数得分。

log_loss(y_true, y_pred, *[, normalize, ...])

Log loss，又称逻辑损失或交叉熵损失。

multilabel_confusion_matrix(y_true, y_pred, *)

计算每个类别或样本的混淆矩阵。

precision_recall_fscore_support(y_true, ...)

计算每个类别的精确度、召回率、F-度量和支持度。

precision_score(y_true, y_pred, *[, labels, ...])

计算精确度。

recall_score(y_true, y_pred, *[, labels, ...])

计算召回率。

roc_auc_score(y_true, y_score, *[, average, ...])

计算从预测分数得到的受试者工作特征曲线（ROC AUC）下的面积。

zero_one_loss(y_true, y_pred, *[, ...])

零一分类损失。

d2_log_loss_score(y_true, y_pred, *[, ...])

\(D^2\) 评分函数，解释的对数损失分数。

还有一些适用于二分类和多标签（但不包括多分类）问题：

average_precision_score(y_true, y_score, *)

计算预测分数的平均精度（AP）。

在以下小节中，我们将描述每个函数，之前会介绍一些通用的API和指标定义。

3.4.5. 从二分类到多分类和多标签#

一些指标本质上是为二分类任务定义的（例如 f1_score , roc_auc_score ）。在这些情况下，默认情况下只评估正类标签，假设正类标签为 1 （尽管这可以通过 pos_label 参数进行配置）。

在将二分类指标扩展到多分类或多标签问题时，数据被视为每个类别的二分类问题的集合。然后有多种方法可以在类别集合上平均二分类指标计算，每种方法在某些场景中可能有用。在可用的情况下，您应该使用 average 参数在这些方法之间进行选择。

  • "macro" 简单地计算二分类指标的平均值，

给予每个类别相同的权重。在那些不常见但重要的类别中，宏观平均可能是一种突出其性能的手段。另一方面，假设所有类别都同等重要往往是不真实的，因此宏观平均会过度强调不常见类别通常较低的性能。

  • "weighted" 通过计算每个类别的二元指标的加权平均来考虑类别不平衡，其中每个类别的分数根据其在真实数据样本中的存在进行加权。

  • "micro" 给予每个样本-类别对总体指标相同的贡献（除了样本权重的影响）。这种方法不是对每个类别的指标进行求和，而是对构成每个类别指标的分子和分母进行求和，以计算总体商。微观平均可能在多标签设置中更受欢迎，包括多类别分类，其中多数类别被忽略。

  • "samples" 仅适用于多标签问题。它不计算每个类别的度量，而是计算评估数据中每个样本的真实类别和预测类别之间的度量，并返回它们的（样本权重加权）平均值。

  • 选择 average=None 将返回一个数组，其中包含每个类别的分数。

虽然多类别数据像二元目标一样以类别标签数组的形式提供给指标，但多标签数据指定为指示矩阵，其中单元格 [i, j] 的值为1，如果样本 i 具有标签 j ，否则为0。

3.4.6. 准确率分数#

accuracy_score 函数计算 准确率 ，即正确预测的比例（默认）或计数（normalize=False）。

在多标签分类中，该函数返回子集准确率。如果一个样本的全部预测标签严格匹配其真实标签， 如果标签集完全匹配，则子集准确度为1.0；否则为0.0。

如果 \(\hat{y}_i\) 是第 \(i\) 个样本的预测值，而 \(y_i\) 是对应的真实值， 那么正确预测的比例在 \(n_\text{samples}\) 上定义为

\[\texttt{accuracy}(y, \hat{y}) = \frac{1}{n_\text{samples}} \sum_{i=0}^{n_\text{samples}-1} 1(\hat{y}_i = y_i)\]

其中 \(1(x)\) 是 指示函数 。

>>> import numpy as np
>>> from sklearn.metrics import accuracy_score
>>> y_pred = [0, 2, 1, 3]
>>> y_true = [0, 1, 2, 3]
>>> accuracy_score(y_true, y_pred)
0.5
>>> accuracy_score(y_true, y_pred, normalize=False)
2.0

在多标签情况下，使用二进制标签指示符:

>>> accuracy_score(np.array([[0, 1], [1, 1]]), np.ones((2, 2)))
0.5

示例

3.4.7. Top-k 准确度评分#

top_k_accuracy_score 函数是 accuracy_score 的泛化。不同之处在于，只要真实标签与 k 个最高预测分数之一相关联，预测就被视为正确。accuracy_score 是 k = 1 的特殊情况。

该函数涵盖二分类和多分类情况，但不包括多标签情况。

如果 \(\hat{f}_{i,j}\) 是第 \(i\) 个样本对应于第 \(j\) 个最大预测分数的预测类别，而 \(y_i\) 是对应的真实值，那么正确预测的比例在 \(n_\text{samples}\) 上定义为

\[\texttt{top-k accuracy}(y, \hat{f}) = \frac{1}{n_\text{samples}} \sum_{i=0}^{n_\text{samples}-1} \sum_{j=1}^{k} 1(\hat{f}_{i,j} = y_i)\]
其中 \(k\) 是允许的猜测次数，\(1(x)\) 是

指示函数 。

>>> import numpy as np
>>> from sklearn.metrics import top_k_accuracy_score
>>> y_true = np.array([0, 1, 2, 2])
>>> y_score = np.array([[0.5, 0.2, 0.2],
...                     [0.3, 0.4, 0.2],
...                     [0.2, 0.4, 0.3],
...                     [0.7, 0.2, 0.1]])
>>> top_k_accuracy_score(y_true, y_score, k=2)
0.75
>>> # 不进行归一化给出“正确”分类的样本数量
>>> top_k_accuracy_score(y_true, y_score, k=2, normalize=False)
3

3.4.8. 平衡准确率得分#

balanced_accuracy_score 函数计算 平衡准确率 ，它避免了在不平衡数据集上的性能估计膨胀。它是每个类别的召回分数的宏平均，或者等价于每个样本根据其真实类别的逆流行度加权的原始准确率。 因此，对于平衡数据集，该得分等于准确率。

在二分类情况下，平衡准确率等于

敏感性

（真正例率）和 特异性 （真负例率）的算术平均值，或者是在二分类预测而不是分数情况下的 ROC 曲线下面积：

\[\texttt{balanced-accuracy} = \frac{1}{2}\left( \frac{TP}{TP + FN} + \frac{TN}{TN + FP}\right )\]

如果分类器在任一类上表现同样良好，这一项简化为常规准确率（即，正确预测的数量除以总预测数量）。

相反，如果常规准确率仅因为分类器利用了不平衡的测试集而高于随机水平，那么平衡 准确性，在适当的情况下，会下降到 \(\frac{1}{n\_classes}\) 。

该评分范围从 0 到 1，或者当使用 adjusted=True 时，它会被重新缩放到 范围 \(\frac{1}{1 - n\_classes}\) 到 1，包括在内，随机性能得分为 0。

如果 \(y_i\) 是第 \(i\) 个样本的真实值，而 \(w_i\) 是对应的样本权重，那么我们将样本权重调整为：

\[\hat{w}_i = \frac{w_i}{\sum_j{1(y_j = y_i) w_j}}\]

其中 \(1(x)\) 是 指示函数 。 给定样本 \(i\) 的预测值 \(\hat{y}_i\) ，平衡准确性定义为：

\[\texttt{balanced-accuracy}(y, \hat{y}, w) = \frac{1}{\sum{\hat{w}_i}} \sum_i 1(\hat{y}_i = y_i) \hat{w}_i\]

当 adjusted=True 时，平衡准确性报告相对于 \(\texttt{balanced-accuracy}(y, \mathbf{0}, w) = \frac{1}{n\_classes}\) 的相对增加。在二分类情况下，这也被称为

或 informedness。

Note

这里的多分类定义似乎是二分类中使用的度量的最合理扩展，尽管在文献中没有确定的共识：

  • 我们的定义：[Mosley2013]，[Kelleher2015] 和 [Guyon2015]，其中 [Guyon2015] 采用了调整版本以确保随机预测得分为 \(0\) ，完美预测得分为 \(1\) 。

  • 如 [Mosley2013] 中所述的类别平衡准确性：计算每个类别之间的精确度和召回率的最小值。然后将这些值在所有类别上平均以获得平衡准确性。

  • 如 [Urbanowicz2015] 中所述的平衡准确性：计算每个类别的敏感性和特异性的平均值，然后在所有类别上平均。

参考文献

[Guyon2015] (1,2)

I. Guyon, K. Bennett, G. Cawley, H.J. Escalante, S. Escalera, T.K. Ho, N. Macià, B. Ray, M. Saeed, A.R. Statnikov, E. Viegas, Design of the 2015 ChaLearn AutoML Challenge , IJCNN 2015.

[Mosley2013] (1,2)

L. Mosley, A balanced approach to the multi-class imbalance problem , IJCV 2010.

3.4.9. Cohen’s kappa#

The function cohen_kappa_score computes Cohen’s kappa statistic. This measure is intended to compare labelings by different human annotators, not a classifier versus a ground truth.

The kappa score is a number between -1 and 1. Scores above .8 are generally considered good agreement; zero or lower means no agreement (practically random labels).

Kappa scores can be computed for binary or multiclass problems, but not for multilabel problems (except by manually computing a per-label score) and not for more than two annotators.

>>> from sklearn.metrics import cohen_kappa_score
>>> labeling1 = [2, 0, 2, 2, 0, 1]
>>> labeling2 = [0, 0, 2, 2, 0, 2]
>>> cohen_kappa_score(labeling1, labeling2)
0.4285714285714286

3.4.10. Confusion matrix#

The confusion_matrix function evaluates classification accuracy by computing the confusion matrix with each row corresponding 到真实类别（Wikipedia和其他参考文献可能使用不同的轴约定）。

根据定义，混淆矩阵中条目 \(i, j\) 是实际属于组 \(i\) 但被预测为属于组 \(j\) 的观测数量。以下是一个示例:

>>> from sklearn.metrics import confusion_matrix
>>> y_true = [2, 0, 2, 2, 0, 1]
>>> y_pred = [0, 0, 2, 2, 0, 2]
>>> confusion_matrix(y_true, y_pred)
array([[2, 0, 0],
       [0, 0, 1],
       [1, 0, 2]])

ConfusionMatrixDisplay 可以用于可视化表示混淆矩阵，如 混淆矩阵 示例所示，该示例创建了以下图形：

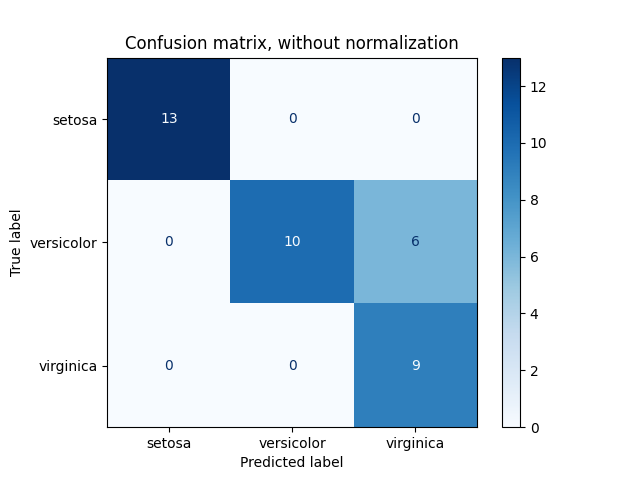
../_images/sphx_glr_plot_confusion_matrix_001.png

参数 normalize 允许报告比率而不是计数。混淆矩阵可以通过三种不同的方式进行归一化： 'pred' 、 'true' 和 'all' ，分别将计数除以每列、每行或整个矩阵的总和。

>>> y_true = [0, 0, 0, 1, 1, 1, 1, 1]
>>> y_pred = [0, 1, 0, 1, 0, 1, 0, 1]
>>> confusion_matrix(y_true, y_pred, normalize='all')
array([[0.25 , 0.125],
       [0.25 , 0.375]])

对于二分类问题，我们可以获取真阴性、假阳性、假阴性和真阳性的计数，如下所示:

>>> y_true = [0, 0, 0, 1, 1, 1, 1, 1]
>>> y_pred = [0, 1, 0, 1, 0, 1, 0, 1]
>>> tn, fp, fn, tp = confusion_matrix(y_true, y_pred).ravel()
>>> tn, fp, fn, tp
(2, 1, 2, 3)

示例

  • 参见 混淆矩阵 以了解使用混淆矩阵评估分类器输出质量的示例。

  • 参见 识别手写数字 以了解使用混淆矩阵进行分类的示例。

手写数字。

3.4.11. 分类报告#

classification_report 函数构建一个文本报告，显示主要的分类指标。以下是一个带有自定义 target_names 和推断标签的小示例:

>>> from sklearn.metrics import classification_report
>>> y_true = [0, 1, 2, 2, 0]
>>> y_pred = [0, 0, 2, 1, 0]
>>> target_names = ['class 0', 'class 1', 'class 2']
>>> print(classification_report(y_true, y_pred, target_names=target_names))
              precision    recall  f1-score   support

     class 0       0.67      1.00      0.80         2
     class 1       0.00      0.00      0.00         1
     class 2       1.00      0.50      0.67         2

    accuracy                           0.60         5
   macro avg       0.56      0.50      0.49         5
weighted avg       0.67      0.60      0.59         5

示例

3.4.12. 汉明损失#

hamming_loss 计算两组样本之间的平均汉明损失或 汉明距离 。

如果 \(\hat{y}_{i,j}\) 是给定样本 \(i\) 的第 \(j\) 个标签的预测值，\(y_{i,j}\) 是对应的真实值，\(n_\text{samples}\) 是样本数量，\(n_\text{labels}\) 是标签的数量，那么汉明损失 \(L_{Hamming}\) 定义为：

\[L_{Hamming}(y, \hat{y}) = \frac{1}{n_\text{samples} * n_\text{labels}} \sum_{i=0}^{n_\text{samples}-1} \sum_{j=0}^{n_\text{labels} - 1} 1(\hat{y}_{i,j} \not= y_{i,j})\]

其中 \(1(x)\) 是 指示函数 。

上述公式在多类分类情况下不成立。更多信息请参阅下面的注释。

>>> from sklearn.metrics import hamming_loss
>>> y_pred = [1, 2, 3, 4]
>>> y_true = [2, 2, 3, 4]
>>> hamming_loss(y_true, y_pred)
0.25

在多标签情况下，使用二进制标签指示符:

>>> hamming_loss(np.array([[0, 1], [1, 1]]), np.zeros((2, 2)))
0.75

Note

在多类分类中，汉明损失对应于 y_true 和 y_pred 之间的汉明距离，类似于 零一损失 函数。然而，零一损失惩罚不严格匹配真实集合的预测集合，而汉明损失惩罚单个标签。因此，汉明损失的上限为零一损失，始终在零和一之间（含）；并且预测真实标签的适当子集或超集将给出零和一之间的汉明损失（不含）。

3.4.13. 精确度、召回率和F度量#

直观上， 精确度 是分类器不将负样本标记为正样本的能力，而

召回率 是分类器找到所有正样本的能力。

F度量

(\(F_\beta\) 和 \(F_1\) 度量) 可以解释为精确度和召回率的加权调和平均数。 \(F_\beta\) 度量在其最佳值为 1，最差值为 0 时达到最佳状态。 当 \(\beta = 1\) 时，\(F_\beta\) 和 \(F_1\) 是等价的，召回率和精确率同等重要。

precision_recall_curve 函数通过改变决策阈值，从真实标签和分类器给出的分数计算精确率-召回率曲线。

average_precision_score 函数计算预测分数的

平均精确率

（AP）。该值介于 0 和 1 之间，值越高越好。AP 定义为

\[\text{AP} = \sum_n (R_n - R_{n-1}) P_n\]

其中 \(P_n\) 和 \(R_n\) 是第 n 个阈值处的精确率和召回率。对于随机预测，AP 是正样本的比例。

参考文献 [Manning2008] 和 [Everingham2010] 提出了精确率-召回率曲线的其他变体。目前， average_precision_score 函数没有实现任何插值变体。参考文献 [Davis2006] 和 [Flach2015] 描述了为什么在精确率-召回率曲线上进行线性插值会提供过于乐观的分类器性能度量。在 auc 中使用梯形法则计算曲线下面积时，会使用这种线性插值。

有多个函数允许你分析精确率、召回率和 F 度量分数：

average_precision_score(y_true, y_score, *)

计算预测分数的平均精度（AP）。

f1_score(y_true, y_pred, *[, labels, ...])

计算F1分数，也称为平衡F-分数或F-度量。

fbeta_score(y_true, y_pred, *, beta[, ...])

计算 F-beta 分数。

precision_recall_curve(y_true[, y_score, ...])

计算不同概率阈值下的精确率-召回率对。

precision_recall_fscore_support(y_true, ...)

计算每个类别的精确度、召回率、F-度量和支持度。

precision_score(y_true, y_pred, *[, labels, ...])

计算精确度。

recall_score(y_true, y_pred, *[, labels, ...])

计算召回率。

请注意，precision_recall_curve 函数仅限于二分类情况。average_precision_score 函数支持多类别和多标签格式，通过以一对多（OvR）方式计算每个类别的分数并根据其 average 参数值进行平均或不平均。

PrecisionRecallDisplay.from_estimator 和 PrecisionRecallDisplay.from_predictions 函数将绘制精确召回曲线，如下所示。

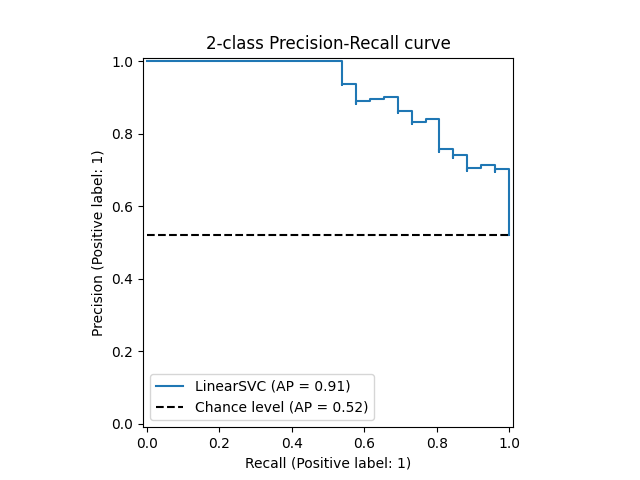
../_images/sphx_glr_plot_precision_recall_001.png

示例

参考文献

[Manning2008]

C.D. Manning, P. Raghavan, H. Schütze, Introduction to Information Retrieval , 2008.

[Everingham2010]

M. Everingham, L. Van Gool, C.K.I. Williams, J. Winn, A. Zisserman, The Pascal Visual Object Classes (VOC) Challenge , IJCV 2010.

在二元分类任务中，术语“正”和“负”指的是分类器的预测，而术语“真”和“假”指的是该预测是否与外部判断（有时称为“观察”）相对应。根据这些定义，我们可以制定以下表格： +——————-+————————————————+ | | 实际类别（观测） | +——————-+———————+————————–+ | 预测类别 | tp（真正例） | fp（假正例） | | （期望） | 正确结果 | 意外结果 | | +———————+————————–+ | | fn（假负例） | tn（真负例） | | | 遗漏结果 | 正确无结果 | +——————-+———————+————————–+

在这个上下文中，我们可以定义精确度和召回率的概念：

\[\text{精确度} = \frac{\text{tp}}{\text{tp} + \text{fp}},\]
\[\text{召回率} = \frac{\text{tp}}{\text{tp} + \text{fn}},\]

（有时召回率也称为“敏感度”）

F-度量是精确度和召回率的加权调和平均值，其中精确度的贡献由某个参数 \(\beta\) 加权：

\[F_\beta = (1 + \beta^2) \frac{\text{精确度} \times \text{召回率}}{\beta^2 \text{精确度} + \text{召回率}}\]

为了避免在精确度和召回率为零时分母为零，Scikit-Learn 使用这个等效公式计算 F-度量：

\[F_\beta = \frac{(1 + \beta^2) \text{tp}}{(1 + \beta^2) \text{tp} + \text{fp} + \beta^2 \text{fn}}\]

请注意，当没有真正例、假正例或假负例时，这个公式仍然是未定义的。默认情况下，对于一组仅包含真负例的集合，F-1 计算为 0，但可以通过 zero_division 参数更改此行为。 以下是二分类的一些小例子:

>>> from sklearn import metrics
>>> y_pred = [0, 1, 0, 0]
>>> y_true = [0, 1, 0, 1]
>>> metrics.precision_score(y_true, y_pred)
1.0
>>> metrics.recall_score(y_true, y_pred)
0.5
>>> metrics.f1_score(y_true, y_pred)
0.66...

>>> metrics.fbeta_score(y_true, y_pred, beta=0.5)
0.83...
>>> metrics.fbeta_score(y_true, y_pred, beta=1)
0.66...
>>> metrics.fbeta_score(y_true, y_pred, beta=2)
0.55...
>>> metrics.precision_recall_fscore_support(y_true, y_pred, beta=0.5)
(array([0.66..., 1.        ]), array([1. , 0.5]), array([0.71..., 0.83...]), array([2, 2]))

>>> import numpy as np
>>> from sklearn.metrics import precision_recall_curve
>>> from sklearn.metrics import average_precision_score
>>> y_true = np.array([0, 0, 1, 1])
>>> y_scores = np.array([0.1, 0.4, 0.35, 0.8])
>>> precision, recall, threshold = precision_recall_curve(y_true, y_scores)
>>> precision
array([0.5       , 0.66..., 0.5       , 1.        , 1.        ])
>>> recall
array([1. , 1. , 0.5, 0.5, 0. ])
>>> threshold
array([0.1 , 0.35, 0.4 , 0.8 ])
>>> average_precision_score(y_true, y_scores)
0.83...

在多类和多标签分类任务中，精确度、召回率和F度量可以独立应用于每个标签。 有几种方法可以跨标签组合结果， 通过传递给 average_precision_score 、f1_score 、 fbeta_score 、precision_recall_fscore_support 、 precision_score 和 recall_score 函数的 average 参数指定，如 上述 所述。

注意以下平均行为：

  • 如果包含所有标签，多类设置中的“微”平均将产生与准确度相同的精确度、召回率和 \(F\) 。

  • “加权”平均可能会产生一个不在精确度和召回率之间的F度量。

  • F度量的“宏”平均计算为每个标签/类F度量的算术平均值，而不是精确度和召回率算术平均值的调和平均值。这两种计算方法在文献中都可以看到，但并不等价，

    参见 [OB2019] 了解详情。

为了更明确地说明，请考虑以下符号：

  • \(y\) 表示 真实 的 \((样本, 标签)\) 对集合

  • \(\hat{y}\) 表示 预测 的 \((样本, 标签)\) 对集合

  • \(L\) 表示标签集合

  • \(S\) 表示样本集合

  • \(y_s\) 表示样本 \(s\) 对应的 \(y\) 子集， 即 \(y_s := \left\{(s', l) \in y | s' = s\right\}\)

  • \(y_l\) 表示标签 \(l\) 对应的 \(y\) 子集

  • 类似地，\(\hat{y}_s\) 和 \(\hat{y}_l\) 是 \(\hat{y}\) 的子集

  • \(P(A, B) := \frac{\left| A \cap B \right|}{\left|B\right|}\) 对于某些集合 \(A\) 和 \(B\)

  • \(R(A, B) := \frac{\left| A \cap B \right|}{\left|A\right|}\) （关于处理 \(A = \emptyset\) 的约定有所不同；此实现使用 \(R(A, B):=0\) ，类似地对于 \(P\) 也是如此。）

  • \(F_\beta(A, B) := \left(1 + \beta^2\right) \frac{P(A, B) \times R(A, B)}{\beta^2 P(A, B) + R(A, B)}\)

然后，指标定义如下：

>>> from sklearn import metrics
>>> y_true = [0, 1, 2, 0, 1, 2]
>>> y_pred = [0, 2, 1, 0, 0, 1]
>>> metrics.precision_score(y_true, y_pred, average='macro')
0.22...
>>> metrics.recall_score(y_true, y_pred, average='micro')
0.33...
>>> metrics.f1_score(y_true, y_pred, average='weighted')
0.26...
>>> metrics.fbeta_score(y_true, y_pred, average='macro', beta=0.5)
0.23...
>>> metrics.precision_recall_fscore_support(y_true, y_pred, beta=0.5, average=None)
(array([0.66..., 0.        , 0.        ]), array([1., 0., 0.]), array([0.71..., 0.        , 0.        ]), array([2, 2, 2]...))

对于多类别分类且包含“负类”的情况，可以排除某些标签：

>>> metrics.recall_score(y_true, y_pred, labels=[1, 2], average='micro')
... # 排除 0，没有标签被正确召回
0.0

类似地，在宏平均中可以考虑数据样本中未出现的标签。

>>> metrics.precision_score(y_true, y_pred, labels=[0, 1, 2, 3], average='macro')
0.166...

参考文献

3.4.14. Jaccard 相似系数得分#

jaccard_score 函数计算 Jaccard 相似系数 的平均值，也称为 Jaccard 指数，在标签集对之间。

Jaccard 相似系数，对于真实标签集 \(y\) 和预测标签集 \(\hat{y}\) ，定义为

\[J(y, \hat{y}) = \frac{|y \cap \hat{y}|}{|y \cup \hat{y}|}.\]

jaccard_score 函数（类似于 precision_recall_fscore_support ）原生应用于二进制目标。通过集合方式计算，它可以扩展应用于多标签和多类分类，通过使用 average 参数（参见 上述 ）。

在二进制情况下:

>>> import numpy as np
>>> from sklearn.metrics import jaccard_score
>>> y_true = np.array([[0, 1, 1],
...                    [1, 1, 0]])
>>> y_pred = np.array([[1, 1, 1],
...                    [1, 0, 0]])
>>> jaccard_score(y_true[0], y_pred[0])
0.6666...

在二维比较情况下（例如图像相似性）：

>>> jaccard_score(y_true, y_pred, average="micro")
0.6

在多标签情况下，使用二进制标签指示器:

>>> jaccard_score(y_true, y_pred, average='samples')
0.5833...
>>> jaccard_score(y_true, y_pred, average='macro')
0.6666...
>>> jaccard_score(y_true, y_pred, average=None)
array([0.5, 0.5, 1. ])

多类问题被二值化并作为相应的多标签问题处理:

>>> y_pred = [0, 2, 1, 2]
>>> y_true = [0, 1, 2, 2]
>>> jaccard_score(y_true, y_pred, average=None)
array([1. , 0. , 0.33...])
>>> jaccard_score(y_true, y_pred, average='macro')
0.44...
>>> jaccard_score(y_true, y_pred, average='micro')
0.33...

3.4.15. Hinge loss#

hinge_loss 函数计算模型与数据之间的平均距离，使用 hinge loss ，这是一种单边度量，仅考虑预测错误。（Hinge loss 用于最大间隔分类器，如支持向量机。）

如果二分类任务中每个样本的真实标签 \(y_i\) 被编码为 \(y_i=\left\{-1, +1\right\}\) ；并且 \(w_i\) 是对应的预测决策（形状为 ( n_samples ,) 的数组，由 decision_function 方法输出），那么 hinge loss 定义为：

\[\]

L_text{Hinge}(y, w) = frac{1}{n_text{samples}} sum_{i=0}^{n_text{samples}-1} maxleft{1 - w_i y_i, 0right}

如果有两个以上的标签，hinge_loss 使用由 Crammer 和 Singer 提出的多类别变体。

这里 是描述它的论文。

在这种情况下，预测的决策是一个形状为 ( n_samples , n_labels ) 的数组。如果 \(w_{i, y_i}\) 是第 \(i\) 个样本的真实标签 \(y_i\) 的预测决策；并且 \(\hat{w}_{i, y_i} = \max\left\{w_{i, y_j}~|~y_j \ne y_i \right\}\) 是所有其他标签的预测决策的最大值，那么多类别铰链损失定义为：

\[L_\text{Hinge}(y, w) = \frac{1}{n_\text{samples}} \sum_{i=0}^{n_\text{samples}-1} \max\left\{1 + \hat{w}_{i, y_i} - w_{i, y_i}, 0\right\}\]

以下是一个小示例，演示了在二分类问题中使用带有 SVM 分类器的 hinge_loss 函数:

>>> from sklearn import svm
>>> from sklearn.metrics import hinge_loss
>>> X = [[0], [1]]
>>> y = [-1, 1]
>>> est = svm.LinearSVC(random_state=0)
>>> est.fit(X, y)
LinearSVC(random_state=0)
>>> pred_decision = est.decision_function([[-2], [3], [0.5]])
>>> pred_decision
array([-2.18...,  2.36...,  0.09...])
>>> hinge_loss([-1, 1, 1], pred_decision)
0.3...

以下是一个示例，演示了在多分类问题中使用带有 SVM 分类器的 hinge_loss 函数:

>>> X = np.array([[0], [1], [2], [3]])
>>> Y = np.array([0, 1, 2, 3])
>>> labels = np.array([0, 1, 2, 3])
>>> est = svm.LinearSVC()
>>> est.fit(X, Y)
LinearSVC()
>>> pred_decision = est.decision_function([[-1], [2], [3]])
>>> y_true = [0, 2, 3]
>>> hinge_loss(y_true, pred_decision, labels=labels)
0.56...

3.4.16. 对数损失#

对数损失，也称为逻辑回归损失或交叉熵损失，定义在概率估计上。 常用於（多項式）邏輯迴歸和神經網絡，以及某些期望最大化算法的變體中，並可用於評估分類器的概率輸出（ predict_proba ），而非其離散預測。

對於具有真實標籤 \(y \in \{0,1\}\) 和概率估計 \(p = \operatorname{Pr}(y = 1)\) 的二元分類，每個樣本的對數損失是分類器在給定真實標籤下的負對數似然：

\[L_{\log}(y, p) = -\log \operatorname{Pr}(y|p) = -(y \log (p) + (1 - y) \log (1 - p))\]

這可以擴展到多類別情況，如下所示。 設一組樣本的真實標籤被編碼為 1-of-K 二元指示矩陣 \(Y\) ， 即如果樣本 \(i\) 具有從 \(K\) 個標籤中取出的標籤 \(k\) ，則 \(y_{i,k} = 1\) 。 設 \(P\) 為概率估計矩陣，其中 \(p_{i,k} = \operatorname{Pr}(y_{i,k} = 1)\) 。 則整個集合的對數損失為

\[L_{\log}(Y, P) = -\log \operatorname{Pr}(Y|P) = - \frac{1}{N} \sum_{i=0}^{N-1} \sum_{k=0}^{K-1} y_{i,k} \log p_{i,k}\]

要了解這如何推廣上述二元對數損失，請注意在二元情況下， \(p_{i,0} = 1 - p_{i,1}\) 和 \(y_{i,0} = 1 - y_{i,1}\) ， 因此展開內部求和項 \(y_{i,k} \in \{0,1\}\) 將給出二元對數損失。

log_loss 函數計算給定真實標籤列表和概率矩陣的對數損失，如估計器的 predict_proba 方法所返回的那樣。

>>> from sklearn.metrics import log_loss
>>> y_true = [0, 0, 1, 1]
>>> y_pred = [[.9, .1], [.8, .2], [.3, .7], [.01, .99]]
>>> log_loss(y_true, y_pred)
0.1738...

y_pred 中的第一個 [.9, .1] 表示第一個樣本具有標籤 0 的概率為 90%。對數損失是非負的。

3.4.17. Matthews 相關係數#

matthews_corrcoef 函數計算

马修相关系数 (MCC)

用于二分类问题。引用维基百科：

“马修相关系数在机器学习中用于衡量二分类（两类）分类的质量。它考虑了真阳性、假阳性和假阴性，通常被认为是一个平衡的度量，即使类别大小非常不同也可以使用。MCC本质上是一个介于-1和+1之间的相关系数值。系数+1表示完美预测，0表示平均随机预测，-1表示反向预测。该统计量也被称为phi系数。”

在二分类（两类）情况下，\(tp\) 、\(tn\) 、\(fp\) 和 \(fn\) 分别是真阳性、真阴性、假阳性和假阴性的数量，MCC定义为

\[MCC = \frac{tp \times tn - fp \times fn}{\sqrt{(tp + fp)(tp + fn)(tn + fp)(tn + fn)}}.\]

在多分类情况下，马修相关系数可以 定义 为针对 \(K\) 类别的 混淆矩阵 \(C\) 。为了简化定义，考虑以下中间变量：

  • \(t_k=\sum_{i}^{K} C_{ik}\) 类别 \(k\) 真正发生的次数，

  • \(p_k=\sum_{i}^{K} C_{ki}\) 类别 \(k\) 被预测的次数，

  • \(c=\sum_{k}^{K} C_{kk}\) 正确预测的样本总数，

  • \(s=\sum_{i}^{K} \sum_{j}^{K} C_{ij}\) 样本总数。

然后多分类MCC定义为：

\[MCC = \frac{ c \times s - \sum_{k}^{K} p_k \times t_k }{\sqrt{ (s^2 - \sum_{k}^{K} p_k^2) \times (s^2 - \sum_{k}^{K} t_k^2) }}\]

当标签多于两个时，MCC的值将不再在-1和+1之间。 在 -1 和 +1 之间。相反，最小值将介于 -1 和 0 之间，具体取决于真实标签的数量和分布。最大值始终为 +1。 有关更多信息，请参阅 [WikipediaMCC2021]。

以下是一个小示例，说明如何使用 matthews_corrcoef 函数：

>>> from sklearn.metrics import matthews_corrcoef
>>> y_true = [+1, +1, +1, -1]
>>> y_pred = [+1, -1, +1, +1]
>>> matthews_corrcoef(y_true, y_pred)
-0.33...

3.4.18. 多标签混淆矩阵#

multilabel_confusion_matrix 函数计算类别的（默认）或多样本的（samplewise=True）多标签混淆矩阵，以评估分类的准确性。multilabel_confusion_matrix 还将多类数据视为多标签数据，因为这种转换通常应用于使用二分类指标（如精确度、召回率等）评估多类问题。

在计算类别的多标签混淆矩阵 \(C\) 时，类别 \(i\) 的真阴性计数为 \(C_{i,0,0}\) ，假阴性为 \(C_{i,1,0}\) ，真正性为 \(C_{i,1,1}\) ，假阳性为 \(C_{i,0,1}\) 。

以下是一个示例，演示如何使用 multilabel_confusion_matrix 函数处理 多标签指示矩阵 输入：

>>> import numpy as np
>>> from sklearn.metrics import multilabel_confusion_matrix
>>> y_true = np.array([[1, 0, 1],
...                    [0, 1, 0]])
>>> y_pred = np.array([[1, 0, 0],
...                    [0, 1, 1]])
>>> multilabel_confusion_matrix(y_true, y_pred)
array([[[1, 0],
        [0, 1]],

       [[1, 0],
        [0, 1]],

       [[0, 1],
        [1, 0]]])

或者可以为每个样本的标签构建一个混淆矩阵：

>>> multilabel_confusion_matrix(y_true, y_pred, samplewise=True)
array([[[1, 0],
        [1, 1]],

       [[1, 1],
        [0, 1]]])

以下是一个示例，演示如何使用 multilabel_confusion_matrix 函数处理 多类 输入：

>>> y_true = ["cat", "ant", "cat", "cat", "ant", "bird"]
>>> y_pred = ["ant", "ant", "cat", "cat", "ant", "cat"]
>>> multilabel_confusion_matrix(y_true, y_pred,
...                             labels=["ant", "bird", "cat"])
array([[[3, 1],
        [0, 2]],

       [[5, 0],
        [1, 0]],

       [[2, 1],
        [1, 2]]])

以下是一些示例，演示如何使用 multilabel_confusion_matrix 函数计算多标签指示矩阵输入问题中每个类别的召回率（或敏感度）、特异性、假阳性率和漏检率。

计算每个类别的 `召回率 <https://en.wikipedia.org/wiki/Sensitivity_and_specificity>`__（也称为真阳性率或敏感度）：

>>> y_true = np.array([[0, 0, 1],
...                    [0, 1, 0],
...                    [1, 1, 0]])
>>> y_pred = np.array([[0, 1, 0],
...                    [0, 0, 1],
...                    [1, 1, 0]])
>>> mcm = multilabel_confusion_matrix(y_true, y_pred)
>>> tn = mcm[:, 0, 0]
>>> tp = mcm[:, 1, 1]
>>> fn = mcm[:, 1, 0]
>>> fp = mcm[:, 0, 1]
>>> tp / (tp + fn)
array([1. , 0.5, 0. ])

计算每个类别的 `特异性 <https://en.wikipedia.org/wiki/Sensitivity_and_specificity>`__（也称为真阴性率）：

>>> tn / (tn + fp)
array([1. , 0. , 0.5])

计算每个类别的 假阳性率 (也称为假阳性率) 对于每个类别:

>>> fp / (fp + tn)
array([0. , 1. , 0.5])

计算 漏报率 (也称为假阴性率) 对于每个类别:

>>> fn / (fn + tp)
array([0. , 0.5, 1. ])

3.4.19. 接收者操作特征 (ROC)#

函数 roc_curve 计算

接收者操作特征曲线，或 ROC 曲线 .

引用维基百科的内容：

“接收者操作特征 (ROC)，或简称为 ROC 曲线，是一个图形，用于说明二分类器系统在其判别阈值变化时的性能。它是通过在不同阈值设置下绘制正例中的真阳性比例 (TPR = 真阳性率) 与负例中的假阳性比例 (FPR = 假阳性率) 来创建的。TPR 也称为灵敏度，FPR 是特异性或真阴性率的补数。”

此函数需要真实的二进制值和目标分数，这些分数可以是正类的概率估计、置信值或二进制决策。以下是一个使用 roc_curve 函数的小示例:

>>> import numpy as np
>>> from sklearn.metrics import roc_curve
>>> y = np.array([1, 1, 2, 2])
>>> scores = np.array([0.1, 0.4, 0.35, 0.8])
>>> fpr, tpr, thresholds = roc_curve(y, scores, pos_label=2)
>>> fpr
array([0. , 0. , 0.5, 0.5, 1. ])
>>> tpr
array([0. , 0.5, 0.5, 1. , 1. ])
>>> thresholds
array([ inf, 0.8 , 0.4 , 0.35, 0.1 ])

与子集准确性、汉明损失或 F1 分数等指标相比，ROC 不需要为每个标签优化阈值。

函数 roc_auc_score ，表示为 ROC-AUC 或 AUROC，计算 ROC曲线下面积。通过这样做，曲线信息被汇总在一个数值中。

下图展示了一个分类器的ROC曲线和ROC-AUC分数，该分类器旨在区分:ref:iris_dataset 中的virginica花与其他物种：

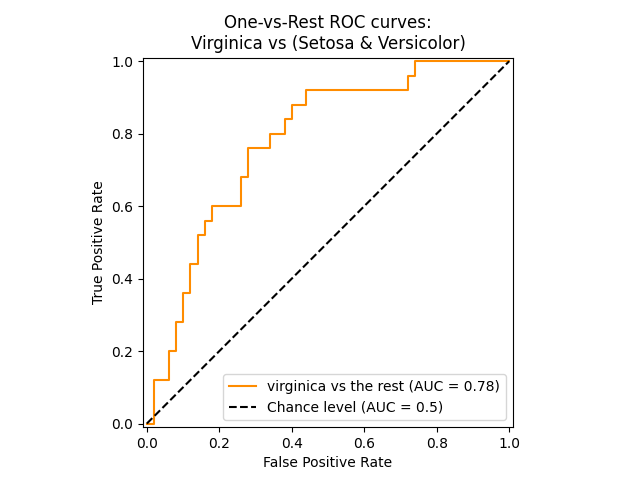
../_images/sphx_glr_plot_roc_001.png

更多信息请参见 Wikipedia关于AUC的文章 。

在**二分类情况**下，你可以提供概率估计值，使用 classifier.predict_proba() 方法，或者使用 classifier.decision_function() 方法提供的无阈值决策值。在提供概率估计的情况下，应提供具有“更大标签”的类的概率。“更大标签”对应于 classifier.classes_[1] ，因此是 classifier.predict_proba(X)[:, 1] 。因此， y_score 参数的大小为(n_samples,)。

>>> from sklearn.datasets import load_breast_cancer
>>> from sklearn.linear_model import LogisticRegression
>>> from sklearn.metrics import roc_auc_score
>>> X, y = load_breast_cancer(return_X_y=True)
>>> clf = LogisticRegression(solver="liblinear").fit(X, y)
>>> clf.classes_
array([0, 1])

我们可以使用对应于 clf.classes_[1] 的概率估计。

>>> y_score = clf.predict_proba(X)[:, 1]
>>> roc_auc_score(y, y_score)
0.99...

否则，我们可以使用无阈值决策值

>>> roc_auc_score(y, clf.decision_function(X))
0.99...

roc_auc_score 函数也可以用于**多分类分类**。目前支持两种平均策略： 一对一算法计算所有可能的成对组合的ROC AUC分数的平均值，而一对多算法计算每个类别相对于所有其他类别的ROC AUC分数的平均值。在这两种情况下，预测标签以一个数组形式提供，其值从0到 n_classes ，并且分数对应于样本属于特定类别的概率估计。OvO和OvR算法支持均匀加权（ average='macro' ）和按流行度加权（ average='weighted' ）。

#一对一算法

计算所有可能的成对组合的平均AUC。[HT2001]_定义了一个均匀加权的多类别AUC指标：

\[\frac{1}{c(c-1)}\sum_{j=1}^{c}\sum_{k > j}^c (\text{AUC}(j | k) + \text{AUC}(k | j))\]

其中 \(c\) 是类别数量，\(\text{AUC}(j | k)\) 是以类别 \(j\) 为正类，类别 \(k\) 为负类的AUC。一般来说， \(\text{AUC}(j | k) \neq \text{AUC}(k | j))\) 在多类别情况下。此算法通过将关键字参数 multiclass 设置为 'ovo' 并将 average 设置为 'macro' 来使用。

[HT2001] 多类别AUC指标可以扩展为按流行度加权：

\[\frac{1}{c(c-1)}\sum_{j=1}^{c}\sum_{k > j}^c p(j \cup k)( \text{AUC}(j | k) + \text{AUC}(k | j))\]

其中 \(c\) 是类别数量。此算法通过将关键字参数 multiclass 设置为 'ovo' 并将 average 设置为 'weighted' 来使用。 'weighted' 选项返回如 [FC2009] 中所述的按流行度加权的平均值。

#一对多算法

计算每个类别相对于其余类别的AUC [PD2000]。该算法在功能上与多标签情况相同。要启用此算法，请将关键字参数 multiclass 设置为 'ovr' 。此外，除了 'macro' [F2006] 和 'weighted' [F2001] 平均外，OvR还支持这些平均方法。

支持 'micro' 平均。

在不能容忍高假阳性率的应用中，可以使用 roc_auc_score 的参数 max_fpr 来汇总 ROC 曲线，直到给定的限制。

下图显示了针对 Iris plants dataset 中不同物种进行区分的分类器的微平均 ROC 曲线及其相应的 ROC-AUC 分数：

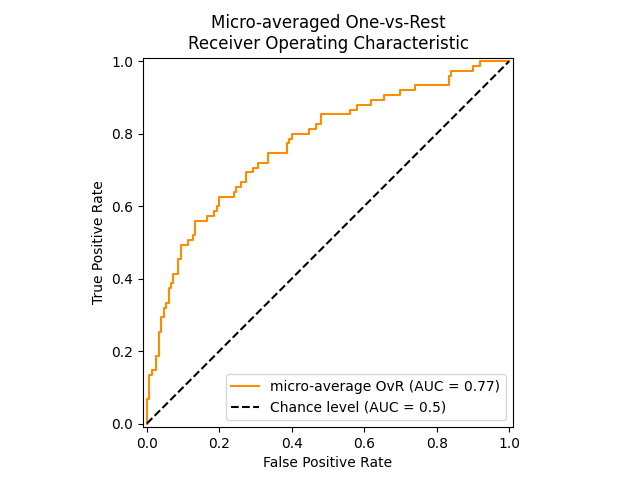
../_images/sphx_glr_plot_roc_002.png

在 多标签分类 中，roc_auc_score 函数通过如 上述 所述的标签平均进行扩展。在这种情况下，你应该提供形状为 (n_samples, n_classes) 的 y_score 。因此，当使用概率估计时，需要为每个输出选择具有更大标签的类的概率。

>>> from sklearn.datasets import make_multilabel_classification
>>> from sklearn.multioutput import MultiOutputClassifier
>>> X, y = make_multilabel_classification(random_state=0)
>>> inner_clf = LogisticRegression(solver="liblinear", random_state=0)
>>> clf = MultiOutputClassifier(inner_clf).fit(X, y)
>>> y_score = np.transpose([y_pred[:, 1] for y_pred in clf.predict_proba(X)])
>>> roc_auc_score(y, y_score, average=None)
array([0.82..., 0.86..., 0.94..., 0.85... , 0.94...])

而决策值不需要这样的处理。

>>> from sklearn.linear_model import RidgeClassifierCV
>>> clf = RidgeClassifierCV().fit(X, y)
>>> y_score = clf.decision_function(X)
>>> roc_auc_score(y, y_score, average=None)
array([0.81..., 0.84... , 0.93..., 0.87..., 0.94...])

示例

参考文献

[HT2001]

Hand, D.J. 和 Till, R.J., (2001). A simple generalisation of the area under the ROC curve for multiple class classification problems. Machine learning, 45(2), pp. 171-186.

[FC2009]

Ferri, Cèsar & Hernandez-Orallo, Jose & Modroiu, R. (2009). An Experimental Comparison of Performance Measures for Classification. Pattern Recognition Letters. 30. 27-38.

[PD2000]

Provost, F., Domingos, P. (2000). Well-trained PETs: Improving probability estimation trees (Section 6.2), CeDER Working Paper #IS-00-04, Stern School of Business, New York University.

[F2006]

Fawcett, T., 2006. An introduction to ROC analysis. Pattern Recognition Letters, 27(8), pp. 861-874.

[F2001]

Fawcett, T., 2001. Using rule sets to maximize ROC performance In Data Mining, 2001. Proceedings IEEE International Conference, pp. 131-138.

3.4.20. 检测错误权衡（DET）#

函数 det_curve 计算检测错误权衡曲线（DET）曲线 [WikipediaDET2017]。 引用自维基百科：

“检测错误权衡（DET）图是一种二元分类系统错误率的图形化表示，绘制假拒绝率与假接受率的关系图。 接受率。x轴和y轴通过其标准正态偏差（或仅通过对数变换）进行非线性缩放，产生比ROC曲线更线性的权衡曲线，并利用大部分图像区域来突出关键操作区域中重要性的差异。

DET曲线是接收操作特征（ROC）曲线的一种变体，其中假阴性率绘制在y轴上，而不是真阳性率。DET曲线通常通过与累积分布函数 \(\phi^{-1}\) （其中 \(\phi\) 是累积分布函数）的变换在正态偏差尺度上绘制。由此产生的性能曲线明确地可视化了给定分类算法的错误类型权衡。参见 [Martin1997] 的示例和进一步动机。

此图比较了两个示例分类器在同一分类任务上的ROC和DET曲线：

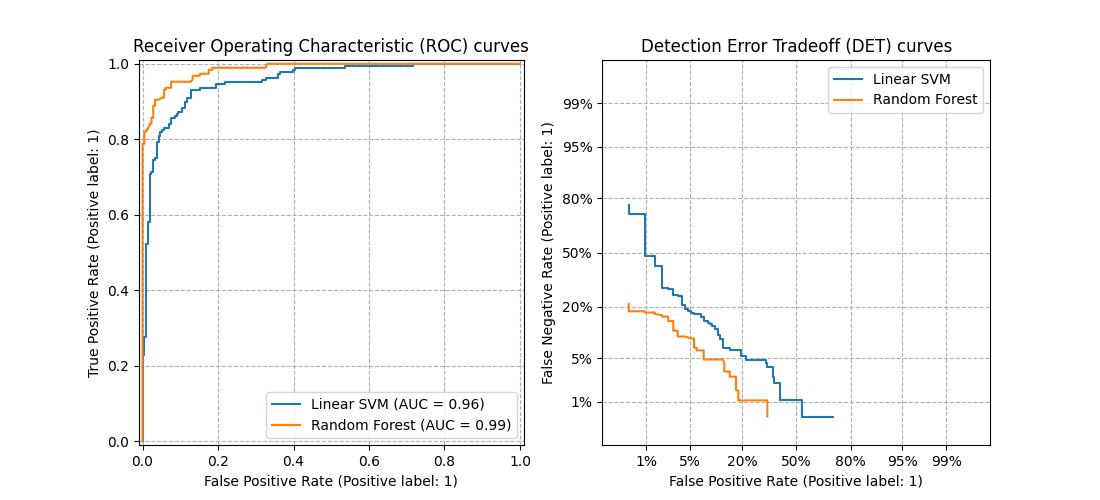
../_images/sphx_glr_plot_det_001.png
#属性

  • 如果检测分数呈正态（或接近正态）分布，DET曲线在正态偏差尺度上形成一条直线。[Navratil2007] 表明反之不一定成立，甚至更一般的分布也能产生线性DET曲线。

  • 正态偏差尺度变换展开了点，使得占据了相对较大的绘图空间。因此，具有相似分类性能的曲线在DET图上可能更容易区分。

  • 由于假阴性率与真阳性率“相反”，DET曲线的完美点是原点（与ROC曲线的左上角相反）。

#应用和局限性

DET曲线易于阅读，因此允许快速直观地评估分类器的性能。

此外，DET曲线可用于阈值分析和操作点选择。 如果在需要比较错误类型的情况下，这一点尤其有用。

另一方面，DET曲线并不提供单一的度量数值。 因此，无论是自动评估还是与其他分类任务进行比较，像ROC曲线下的衍生面积这样的度量可能更适合。

示例

参考文献

[WikipediaDET2017]

Wikipedia贡献者。检测错误权衡。 Wikipedia, The Free Encyclopedia. 2017年9月4日，23:33 UTC。 可访问于：https://en.wikipedia.org/w/index.php?title=Detection_error_tradeoff&oldid=798982054。 访问于2018年2月19日。

[Martin1997]

A. Martin, G. Doddington, T. Kamm, M. Ordowski, 和 M. Przybocki, The DET Curve in Assessment of Detection Task Performance , NIST 1997.

3.4.21. 零一损失#

zero_one_loss 函数计算0-1分类损失（\(L_{0-1}\) ）在 \(n_{\text{samples}}\) 上的总和或平均值。 默认情况下，该函数对样本进行归一化处理。要获取 \(L_{0-1}\) 的总和，请将 normalize 设置为 False 。

在多标签分类中，zero_one_loss 将子集评分为一，如果其标签严格匹配预测结果， 并且如果有任何错误则评分为零。默认情况下，该函数返回不完美匹配的百分比。 预测子集的数量。如果需要获取这些子集的数量而不是归一化值，请将 normalize 设置为 False 。

如果 \(\hat{y}_i\) 是第 \(i\) 个样本的预测值，而 \(y_i\) 是对应的真实值，那么 0-1 损失 \(L_{0-1}\) 定义为：

\[L_{0-1}(y, \hat{y}) = \frac{1}{n_\text{samples}} \sum_{i=0}^{n_\text{samples}-1} 1(\hat{y}_i \not= y_i)\]

其中 \(1(x)\) 是 指示函数 。零一损失也可以计算为 \(zero-one loss = 1 - accuracy\) 。

>>> from sklearn.metrics import zero_one_loss
>>> y_pred = [1, 2, 3, 4]
>>> y_true = [2, 2, 3, 4]
>>> zero_one_loss(y_true, y_pred)
0.25
>>> zero_one_loss(y_true, y_pred, normalize=False)
1.0

在多标签情况下，使用二进制标签指示器，其中第一个标签集 [0,1] 有一个错误：

>>> zero_one_loss(np.array([[0, 1], [1, 1]]), np.ones((2, 2)))
0.5

>>> zero_one_loss(np.array([[0, 1], [1, 1]]), np.ones((2, 2)),  normalize=False)
1.0

示例

3.4.22. Brier 分数损失#

brier_score_loss 函数计算二分类的 Brier 分数 [Brier1950]。引用自维基百科：

“Brier 分数是一个适当的评分函数，用于衡量概率预测的准确性。它适用于预测必须为一组互斥的离散结果分配概率的任务。”

该函数返回实际结果 \(y \in \{0,1\}\) 和预测概率估计 \(p = \operatorname{Pr}(y = 1)\) (predict_proba ) 的均方误差，计算公式如下：

\[BS = \frac{1}{n_{\text{samples}}} \sum_{i=0}^{n_{\text{samples}} - 1}(y_i - p_i)^2\]

Brier 分数损失也在 0 到 1 之间，值越低（均方差越小），预测越准确。

以下是该函数使用的一个小示例:

>>> import numpy as np
>>> from sklearn.metrics import brier_score_loss
>>> y_true = np.array([0, 1, 1, 0])
>>> y_true_categorical = np.array(["spam", "ham", "ham", "spam"])
>>> y_prob = np.array([0.1, 0.9, 0.8, 0.4])
>>> y_pred = np.array([0, 1, 1, 0])
>>> brier_score_loss(y_true, y_prob)
0.055
>>> brier_score_loss(y_true, 1 - y_prob, pos_label=0)
0.055
>>> brier_score_loss(y_true_categorical, y_prob, pos_label="ham")
0.055
>>> brier_score_loss(y_true, y_prob > 0.5)
0.0

Brier 分数可用于评估分类器的校准程度。然而，较低的 Brier 分数损失并不总是意味着更好的校准。这是因为，类比于均方误差的偏差-方差分解，Brier 分数损失可以分解为校准损失和细化损失 [Bella2012]。校准损失定义为与从 ROC 段斜率得出的经验概率的均方偏差。细化损失可以定义为按最优成本曲线下的面积测量的预期最优损失。细化损失可以独立于校准损失变化，因此较低的 Brier 分数损失并不一定意味着更好的校准模型。“只有在细化损失保持不变时，较低的 Brier 分数损失才总是意味着更好的校准” [Bella2012], [Flach2008]。

示例

参考文献

[Brier1950]

  1. Brier, `Verification of forecasts expressed in terms of probability

<ftp://ftp.library.noaa.gov/docs.lib/htdocs/rescue/mwr/078/mwr-078-01-0001.pdf>`_ , 月度天气回顾 78.1 (1950)

[Bella2012] (1,2)

Bella, Ferri, Hernández-Orallo, and Ramírez-Quintana “机器学习模型的校准” 在 Khosrow-Pour, M. “机器学习：概念、方法论、工具和应用.” Hershey, PA: 信息科学参考 (2012).

[Flach2008]

Flach, Peter, and Edson Matsubara. “关于分类、排序和概率估计.” Dagstuhl 研讨会论文集. Schloss Dagstuhl-Leibniz 信息中心 (2008).

3.4.23. 类别似然比#

class_likelihood_ratios 函数计算二分类的 正负似然比 \(LR_\pm\) ，可以解释为后验概率与先验概率的比率，如下所述。因此，该指标相对于类别先验概率（正类样本数除以总样本数）是不变的，并且可以在不同群体之间外推，无论是否存在类别不平衡。

因此，\(LR_\pm\) 指标在数据可用性受限的情况下非常有用，例如在类几乎平衡的研究人群中学习并评估分类器，而目标应用（即一般人群）的先验概率非常低。

正似然比 \(LR_+\) 是分类器正确预测样本属于正类的概率除以预测正类样本属于负类的概率：

\[LR_+ = \frac{\text{PR}(P+|T+)}{\text{PR}(P+|T-)}.\]

这里的符号表示预测（\(P\) ）或真实（\(T\) ）标签，而符号 \(+\) 和 \(-\) 分别表示正类和负类，例如 \(P+\) 表示“预测为正类”。

类似地，负似然比 \(LR_-\) 是一个正类样本被分类为属于负类的概率除以一个负类样本被正确分类的概率：

\[LR_- = \frac{\text{PR}(P-|T+)}{\text{PR}(P-|T-)}.\]

对于高于机会水平的分类器，\(LR_+\) 大于1 越高越好，而 \(LR_-\) 范围从0到1 越低越好。 \(LR_\pm\approx 1\) 的值对应于机会水平。

请注意，概率与计数不同，例如 \(\operatorname{PR}(P+|T+)\) 不等于真阳性计数 tp （参见 维基百科页面 以获取实际公式）。

示例

#不同患病率下的解释

两个类别的似然比都可以根据优势比（前测和后测）进行解释：

\[\text{后测优势} = \text{似然比} \times \text{前测优势}.\]

优势通常通过以下方式与概率相关：

\[\text{优势} = \frac{\text{概率}}{1 - \text{概率}},\]

或者等价地

\[\text{概率} = \frac{\text{优势}}{1 + \text{优势}}.\]

在给定的人群中，前测概率由患病率给出。通过将优势转换为概率，似然比可以转换为在分类器预测前后真正属于任一类的概率：

\[\text{后测优势} = \text{似然比} \times \frac{\text{前测概率}}{1 - \text{前测概率}},\]
\[\text{后验概率} = \frac{\text{后验几率}}{1 + \text{后验几率}}.\]
#数学分歧

当 \(fp = 0\) 时，阳性似然比未定义，这可以解释为分类器完美地识别了阳性案例。如果 \(fp = 0\) 并且还 \(tp = 0\) ，这将导致零除以零的情况。例如，当使用总是预测负类的 DummyClassifier 时，就会发生这种情况，因此将其解释为完美分类器就失去了意义。

当 \(tn = 0\) 时，阴性似然比未定义。这种分歧是无效的，因为 \(LR_- > 1\) 会表明在样本被分类为负类后，属于正类的几率增加，就好像分类行为导致了正类条件一样。这包括 DummyClassifier 总是预测正类的情况（即当 \(tn=fn=0\) 时）。

当 \(tp=fn=0\) 时，两个类别的似然比都未定义，这意味着测试集中没有正类样本。当交叉验证高度不平衡的数据时，也可能发生这种情况。

在所有上述情况下，默认情况下，class_likelihood_ratios 函数会引发适当的警告消息并返回 nan ，以避免在交叉验证折叠中进行平均时受到污染。

有关 class_likelihood_ratios 函数的工作示例，请参见下面的示例。

#参考文献

3.4.24. 分类的 D² 分数#

D² 分数计算了可解释的偏差比例。 它是 R² 的泛化，其中平方误差被泛化并替换为选择的分类偏差 \(\text{dev}(y, \hat{y})\) （例如，对数损失）。D² 是一种 技能分数。 其计算公式为

\[D^2(y, \hat{y}) = 1 - \frac{\text{dev}(y, \hat{y})}{\text{dev}(y, y_{\text{null}})} \,.\]

其中 \(y_{\text{null}}\) 是仅截距模型的最优预测 （例如，在对数损失情况下， y_true 的每个类别的比例）。

与 R² 类似，最佳分数为 1.0，并且它可以为负（因为模型可能任意更差）。一个始终预测 \(y_{\text{null}}\) 的常数模型，忽略输入特征，将获得 0.0 的 D² 分数。

#D2 对数损失分数

d2_log_loss_score 函数实现了 D² 的特殊情况，使用对数损失，参见 对数损失 ，即：

\[\text{dev}(y, \hat{y}) = \text{log_loss}(y, \hat{y}).\]

以下是 d2_log_loss_score 函数的一些使用示例:

>>> from sklearn.metrics import d2_log_loss_score
>>> y_true = [1, 1, 2, 3]
>>> y_pred = [
...    [0.5, 0.25, 0.25],
...    [0.5, 0.25, 0.25],
...    [0.5, 0.25, 0.25],
...    [0.5, 0.25, 0.25],
... ]
>>> d2_log_loss_score(y_true, y_pred)
0.0
>>> y_true = [1, 2, 3]
>>> y_pred = [
...     [0.98, 0.01, 0.01],
...     [0.01, 0.98, 0.01],
...     [0.01, 0.01, 0.98],
... ]
>>> d2_log_loss_score(y_true, y_pred)
0.981...
>>> y_true = [1, 2, 3]
>>> y_pred = [
...     [0.1, 0.6, 0.3],
...     [0.1, 0.6, 0.3],
...     [0.4, 0.5, 0.1],
... ]
>>> d2_log_loss_score(y_true, y_pred)
-0.552...

3.4.24.1. 多标签排序指标#

在多标签学习中，每个样本可以有任意数量的真实标签 与之相关。目标是给予真实标签高分数和更好的排名。

3.4.25. 覆盖误差#

coverage_error 函数计算在最终预测中必须包含的标签的平均数量，以确保所有真实标签都被预测。如果你想了解在不遗漏任何真实标签的情况下，平均需要预测多少个最高分数的标签，这个指标就很有用。因此，这个指标的最佳值是真实标签的平均数量。

Note

我们的实现得分比 Tsoumakas 等人在2010年给出的得分大1。这扩展了它以处理实例没有真实标签的退化情况。

形式上，给定真实标签的二进制指示矩阵 \(y \in \left\{0, 1\right\}^{n_\text{samples} \times n_\text{labels}}\) 和每个标签的分数 \(\hat{f} \in \mathbb{R}^{n_\text{samples} \times n_\text{labels}}\) ，覆盖率定义为

\[coverage(y, \hat{f}) = \frac{1}{n_{\text{samples}}} \sum_{i=0}^{n_{\text{samples}} - 1} \max_{j:y_{ij} = 1} \text{rank}_{ij}\]

其中 \(\text{rank}_{ij} = \left|\left\{k: \hat{f}_{ik} \geq \hat{f}_{ij} \right\}\right|\) 。根据排名定义， y_scores 中的平局通过给予所有平局值中最大的排名来打破。

这是一个使用该函数的小例子:

>>> import numpy as np
>>> from sklearn.metrics import coverage_error
>>> y_true = np.array([[1, 0, 0], [0, 0, 1]])
>>> y_score = np.array([[0.75, 0.5, 1], [1, 0.2, 0.1]])
>>> coverage_error(y_true, y_score)
2.5

3.4.26. 标签排名平均精度#

label_ranking_average_precision_score 函数实现了标签排名平均精度（LRAP）。这个指标与 average_precision_score 函数相关，但基于标签排名的概念。 标签排名而非精确度和召回率。

标签排名平均精度（LRAP）通过对样本的平均来回答以下问题：对于每个真实标签，排名更高的标签中有多少是真实标签？如果你能更好地对每个样本关联的标签进行排名，这种性能指标将会更高。获得的分数总是严格大于0，最佳值为1。如果每个样本恰好有一个相关标签，标签排名平均精度等价于 平均倒数排名 。

形式上，给定真实标签的二进制指示矩阵 \(y \in \left\{0, 1\right\}^{n_\text{samples} \times n_\text{labels}}\) 和每个标签的分数 \(\hat{f} \in \mathbb{R}^{n_\text{samples} \times n_\text{labels}}\) ，平均精度定义为

\[LRAP(y, \hat{f}) = \frac{1}{n_{\text{samples}}} \sum_{i=0}^{n_{\text{samples}} - 1} \frac{1}{||y_i||_0} \sum_{j:y_{ij} = 1} \frac{|\mathcal{L}_{ij}|}{\text{rank}_{ij}}\]

其中 \(\mathcal{L}_{ij} = \left\{k: y_{ik} = 1, \hat{f}_{ik} \geq \hat{f}_{ij} \right\}\) ， \(\text{rank}_{ij} = \left|\left\{k: \hat{f}_{ik} \geq \hat{f}_{ij} \right\}\right|\) ， \(|\cdot|\) 计算集合的基数（即集合中元素的数量），而 \(||\cdot||_0\) 是 \(\ell_0\) “范数”（计算向量中非零元素的数量）。

以下是该函数使用的一个小示例:

>>> import numpy as np
>>> from sklearn.metrics import label_ranking_average_precision_score
>>> y_true = np.array([[1, 0, 0], [0, 0, 1]])
>>> y_score = np.array([[0.75, 0.5, 1], [1, 0.2, 0.1]])
>>> label_ranking_average_precision_score(y_true, y_score)
0.416...

3.4.27. 排名损失#

label_ranking_loss 函数计算排名损失，该损失 对样本进行平均，计算标签对中顺序错误的数量，即真实标签的得分低于虚假标签的得分，权重为虚假标签和真实标签的有序对数的倒数。可达到的最低排名损失为零。

形式上，给定地面真实标签的二进制指示矩阵 \(y \in \left\{0, 1\right\}^{n_\text{samples} \times n_\text{labels}}\) 和与每个标签相关的得分 \(\hat{f} \in \mathbb{R}^{n_\text{samples} \times n_\text{labels}}\) ，排名损失定义为

\[ranking\_loss(y, \hat{f}) = \frac{1}{n_{\text{samples}}} \sum_{i=0}^{n_{\text{samples}} - 1} \frac{1}{||y_i||_0(n_\text{labels} - ||y_i||_0)} \left|\left\{(k, l): \hat{f}_{ik} \leq \hat{f}_{il}, y_{ik} = 1, y_{il} = 0 \right\}\right|\]

其中 \(|\cdot|\) 计算集合的基数（即集合中元素的数量），\(||\cdot||_0\) 是 \(\ell_0\) “范数”（计算向量中非零元素的数量）。

以下是该函数使用的一个小示例:

>>> import numpy as np
>>> from sklearn.metrics import label_ranking_loss
>>> y_true = np.array([[1, 0, 0], [0, 0, 1]])
>>> y_score = np.array([[0.75, 0.5, 1], [1, 0.2, 0.1]])
>>> label_ranking_loss(y_true, y_score)
0.75...
>>> # 使用以下预测，我们得到完美的最小损失
>>> y_score = np.array([[1.0, 0.1, 0.2], [0.1, 0.2, 0.9]])
>>> label_ranking_loss(y_true, y_score)
0.0
#参考文献

  • Tsoumakas, G., Katakis, I., & Vlahavas, I. (2010). Mining multi-label data. In Data mining and knowledge discovery handbook (pp. 667-685). Springer US.

3.4.28. 归一化折损累积增益#

折损累积增益（DCG）和归一化折损累积增益（NDCG）是在 dcg_score 中实现的排名指标。 和 ndcg_score ；它们将预测的顺序与基本事实分数进行比较，例如查询答案的相关性。

从维基百科关于折扣累积增益的页面：

“折扣累积增益（DCG）是衡量排序质量的一种方法。在信息检索中，它常用于衡量网络搜索引擎算法或相关应用的有效性。使用搜索结果集中文档的等级相关性尺度，DCG衡量文档在结果列表中的位置的有用性或增益。增益从结果列表的顶部累积到底部，每个结果的增益在较低的排名中进行折扣”

DCG 按照预测的顺序排列真实目标（例如查询答案的相关性），然后将其乘以对数衰减并求和。这个和可以在前 \(K\) 个结果后截断，在这种情况下我们称之为 DCG@K。 NDCG 或 NDCG@K 是 DCG 除以完美预测得到的 DCG，因此它总是在 0 和 1 之间。通常，NDCG 比 DCG 更受欢迎。

与排序损失相比，NDCG 可以考虑相关性分数，而不是基本事实排序。因此，如果基本事实仅包含一个顺序，则应首选排序损失；如果基本事实包含实际的有用性分数（例如，0 表示不相关，1 表示相关，2 表示非常相关），则可以使用 NDCG。

对于一个样本，给定每个目标的连续基本事实值向量 \(y \in \mathbb{R}^{M}\) ，其中 \(M\) 是输出的数量，以及预测 \(\hat{y}\) ，它诱导排序函数 \(f\) ，DCG 分数是

\[\sum_{r=1}^{\min(K, M)}\frac{y_{f(r)}}{\log(1 + r)}\]

而 NDCG 分数是 DCG 分数除以 \(y\) 得到的 DCG 分数。

#参考文献

  • Jarvelin, K., & Kekalainen, J. (2002). 基于累积增益的IR技术评估。ACM信息系统交易(TOIS)，20(4)，422-446。

  • Wang, Y., Wang, L., Li, Y., He, D., Chen, W., & Liu, T. Y. (2013年5月)。 NDCG排序度量的理论分析。在第26届学习理论年会(COLT 2013)会议记录中

  • McSherry, F., & Najork, M. (2008年3月)。在存在平局分数的情况下高效计算信息检索性能度量。在欧洲信息检索会议(pp. 414-421)。Springer, 柏林, 海德堡。

3.4.28.1. 回归度量#

sklearn.metrics 模块实现了多个用于衡量回归性能的损失、评分和效用函数。其中一些已经增强以处理多输出情况：mean_squared_error 、 mean_absolute_error 、r2_score 、 explained_variance_score 、mean_pinball_loss 、d2_pinball_score 和:func:d2_absolute_error_score 。

这些函数有一个 multioutput 关键字参数，用于指定如何平均每个单独目标的分数或损失。默认值为 'uniform_average' ，表示对输出进行均匀加权的平均。如果传递了一个形状为 (n_outputs,) 的 ndarray ，则其条目被解释为权重，并返回相应的加权平均值。如果 multioutput 为 'raw_values' ，则所有未改变的单个分数或损失将以形状为 (n_outputs,) 的数组形式返回。

r2_score 和:func:explained_variance_score 接受一个额外的值 'variance_weighted' 作为 multioutput 参数。此选项导致每个单独的分数按相应目标变量的方差进行加权。此设置量化了全局捕获的 未缩放方差。如果目标变量的尺度不同，那么这个评分会更加重视解释高方差变量。

3.4.29. R² 评分，决定系数#

r2_score 函数计算 决定系数 ，通常表示为 \(R^2\) 。

它表示模型中自变量解释的方差（y的）比例。它提供了拟合优度的指示，因此是衡量模型对未见样本预测能力的指标，通过解释方差的比例来体现。

由于方差依赖于数据集，\(R^2\) 在不同数据集之间可能没有意义地可比较。最佳可能得分是 1.0，它也可能是负的（因为模型可能任意地更差）。一个总是预测 y 的期望（平均）值的常数模型，忽略输入特征，将得到 \(R^2\) 得分为 0.0。

注意：当预测残差的均值为零时，\(R^2\) 评分和 explained_variance_score 是相同的。

如果 \(\hat{y}_i\) 是第 \(i\) 个样本的预测值，而 \(y_i\) 是对应的真实值，总共有 \(n\) 个样本，估计的 \(R^2\) 定义为：

\[R^2(y, \hat{y}) = 1 - \frac{\sum_{i=1}^{n} (y_i - \hat{y}_i)^2}{\sum_{i=1}^{n} (y_i - \bar{y})^2}\]

其中 \(\bar{y} = \frac{1}{n} \sum_{i=1}^{n} y_i\) 且 \(\sum_{i=1}^{n} (y_i - \hat{y}_i)^2 = \sum_{i=1}^{n} \epsilon_i^2\) 。

注意 r2_score 计算未调整的 \(R^2\) ，不修正 y 样本方差中的偏差。

在真实目标为常数的特定情况下，\(R^2\) 评分不是有限的：它要么是 NaN （完美预测），要么是 -Inf （不完美预测）。这种非有限评分可能妨碍正确的模型优化。 例如，为了正确执行网格搜索交叉验证。出于这个原因，r2_score 的默认行为是将它们替换为 1.0（完美预测）或 0.0（不完美预测）。如果 force_finite 设置为 False ，则该评分会回退到原始的 \(R^2\) 定义。

以下是一个 r2_score 函数使用的小示例:

>>> from sklearn.metrics import r2_score
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> r2_score(y_true, y_pred)
0.948...
>>> y_true = [[0.5, 1], [-1, 1], [7, -6]]
>>> y_pred = [[0, 2], [-1, 2], [8, -5]]
>>> r2_score(y_true, y_pred, multioutput='variance_weighted')
0.938...
>>> y_true = [[0.5, 1], [-1, 1], [7, -6]]
>>> y_pred = [[0, 2], [-1, 2], [8, -5]]
>>> r2_score(y_true, y_pred, multioutput='uniform_average')
0.936...
>>> r2_score(y_true, y_pred, multioutput='raw_values')
array([0.965..., 0.908...])
>>> r2_score(y_true, y_pred, multioutput=[0.3, 0.7])
0.925...
>>> y_true = [-2, -2, -2]
>>> y_pred = [-2, -2, -2]
>>> r2_score(y_true, y_pred)
1.0
>>> r2_score(y_true, y_pred, force_finite=False)
nan
>>> y_true = [-2, -2, -2]
>>> y_pred = [-2, -2, -2 + 1e-8]
>>> r2_score(y_true, y_pred)
0.0
>>> r2_score(y_true, y_pred, force_finite=False)
-inf

示例

3.4.30. 平均绝对误差#

mean_absolute_error 函数计算 平均绝对误差 ，这是一种风险度量，对应于绝对误差损失或 \(l1\) -范数损失的期望值。

如果 \(\hat{y}_i\) 是第 \(i\) 个样本的预测值，而 \(y_i\) 是对应的真实值，那么平均绝对误差 (MAE) 在 \(n_{\text{samples}}\) 上的估计定义为

\[\text{MAE}(y, \hat{y}) = \frac{1}{n_{\text{samples}}} \sum_{i=0}^{n_{\text{samples}}-1} \left| y_i - \hat{y}_i \right|.\]

以下是 mean_absolute_error 函数使用的一个小例子:

>>> from sklearn.metrics import mean_absolute_error
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> mean_absolute_error(y_true, y_pred)
0.5
>>> y_true = [[0.5, 1], [-1, 1], [7, -6]]
>>> y_pred = [[0, 2], [-1, 2], [8, -5]]
>>> mean_absolute_error(y_true, y_pred)
0.75
>>> mean_absolute_error(y_true, y_pred, multioutput='raw_values')
array([0.5, 1. ])
>>> mean_absolute_error(y_true, y_pred, multioutput=[0.3, 0.7])
0.85...

3.4.31. 均方误差#

mean_squared_error 函数计算 均方误差 ，这是一种对应于平方（二次）误差或损失的期望值的风险度量。

如果 \(\hat{y}_i\) 是第 \(i\) 个样本的预测值，而 \(y_i\) 是对应的真实值，那么在 \(n_{\text{samples}}\) 上的均方误差（MSE）估计定义为

\[\text{MSE}(y, \hat{y}) = \frac{1}{n_\text{samples}} \sum_{i=0}^{n_\text{samples} - 1} (y_i - \hat{y}_i)^2.\]

以下是 mean_squared_error 函数使用的一个小例子:

>>> from sklearn.metrics import mean_squared_error
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> mean_squared_error(y_true, y_pred)
0.375
>>> y_true = [[0.5, 1], [-1, 1], [7, -6]]
>>> y_pred = [[0, 2], [-1, 2], [8, -5]]
>>> mean_squared_error(y_true, y_pred)
0.7083...

示例

  • 参见 梯度提升回归 以查看使用均方误差评估梯度提升回归的示例。

取MSE的平方根，称为均方根误差（RMSE），是另一种常用指标，它以与目标变量相同的单位提供度量。RMSE可通过 root_mean_squared_error 函数获得。

3.4.32. 均方对数误差#

mean_squared_log_error 函数计算与平方对数（二次）误差或损失的期望值相对应的风险度量。

如果 \(\hat{y}_i\) 是第 \(i\) 个样本的预测值，而 \(y_i\) 是对应的真实值，那么均方对数误差（MSLE）在 \(n_{\text{samples}}\) 上的估计定义为

\[\text{MSLE}(y, \hat{y}) = \frac{1}{n_\text{samples}} \sum_{i=0}^{n_\text{samples} - 1} (\log_e (1 + y_i) - \log_e (1 + \hat{y}_i) )^2.\]

其中 \(\log_e (x)\) 表示 \(x\) 的自然对数。当目标具有指数增长时，例如人口数量、某商品在多年期间的平均销售量等，此度量指标最为适用。请注意，此度量对预测不足的估计比预测过度的估计惩罚更大。

以下是 mean_squared_log_error 函数使用的一个小示例:

>>> from sklearn.metrics import mean_squared_log_error
>>> y_true = [3, 5, 2.5, 7]
>>> y_pred = [2.5, 5, 4, 8]
>>> mean_squared_log_error(y_true, y_pred)
0.039...
>>> y_true = [[0.5, 1], [1, 2], [7, 6]]
>>> y_pred = [[0.5, 2], [1, 2.5], [8, 8]]
>>> mean_squared_log_error(y_true, y_pred)
0.044...

均方根对数误差（RMSLE）可通过 root_mean_squared_log_error 函数获得。

3.4.33. 平均绝对百分比误差#

mean_absolute_percentage_error （MAPE），也称为平均绝对百分比偏差（MAPD），是回归问题的评估度量。 这个指标的目的是对相对误差敏感。例如，它不会因为目标变量的全局缩放而改变。

如果 \(\hat{y}_i\) 是第 \(i\) 个样本的预测值，而 \(y_i\) 是对应的真实值，那么平均绝对百分比误差（MAPE）在 \(n_{\text{samples}}\) 上估计为

\[\text{MAPE}(y, \hat{y}) = \frac{1}{n_{\text{samples}}} \sum_{i=0}^{n_{\text{samples}}-1} \frac{{}\left| y_i - \hat{y}_i \right|}{\max(\epsilon, \left| y_i \right|)}\]

其中 \(\epsilon\) 是一个任意小但严格为正的数，以避免当 y 为零时结果未定义。

mean_absolute_percentage_error 函数支持多输出。

以下是一个使用 mean_absolute_percentage_error 函数的小示例:

>>> from sklearn.metrics import mean_absolute_percentage_error
>>> y_true = [1, 10, 1e6]
>>> y_pred = [0.9, 15, 1.2e6]
>>> mean_absolute_percentage_error(y_true, y_pred)
0.2666...

在上面的示例中，如果我们使用了 mean_absolute_error ，它会忽略小幅度值，只反映最大幅度值的预测误差。但这个问题在 MAPE 中得到了解决，因为它计算的是相对于实际输出的相对百分比误差。

3.4.34. 中位数绝对误差#

median_absolute_error 特别有趣，因为它对异常值具有鲁棒性。损失是通过取目标和预测之间所有绝对差异的中位数来计算的。

如果 \(\hat{y}_i\) 是第 \(i\) 个样本的预测值，而 \(y_i\) 是对应的真实值，那么中位数绝对误差（MedAE）在 \(n_{\text{samples}}\) 上估计为

\[\text{MedAE}(y, \hat{y}) = \text{median}(\mid y_1 - \hat{y}_1 \mid, \ldots, \mid y_n - \hat{y}_n \mid).\]

median_absolute_error 不支持多输出。 以下是 median_absolute_error 函数使用的一个小示例:

>>> from sklearn.metrics import median_absolute_error
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> median_absolute_error(y_true, y_pred)
0.5



  解释方差得分与 :ref:`r2_score` 之间的区别在于，解释方差得分不考虑预测中的系统偏移。因此，通常情况下应优先选择 :ref:`r2_score` 。

在真实目标为常数的特定情况下，解释方差得分不是有限的：它要么是 NaN （完美预测），要么是 -Inf （不完美预测）。这种非有限的得分可能阻止正确的模型优化，如网格搜索交叉验证的正确执行。出于这个原因，explained_variance_score 的默认行为是用 1.0（完美预测）或 0.0（不完美预测）替换它们。你可以将 force_finite 参数设置为 False ，以防止这种修复发生，并回退到原始的解释方差得分。

以下是一个使用 explained_variance_score 函数的小示例:

>>> from sklearn.metrics import explained_variance_score
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> explained_variance_score(y_true, y_pred)
0.957...
>>> y_true = [[0.5, 1], [-1, 1], [7, -6]]
>>> y_pred = [[0, 2], [-1, 2], [8, -5]]
>>> explained_variance_score(y_true, y_pred, multioutput='raw_values')
array([0.967..., 1.        ])
>>> explained_variance_score(y_true, y_pred, multioutput=[0.3, 0.7])
0.990...
>>> y_true = [-2, -2, -2]
>>> y_pred = [-2, -2, -2]
>>> explained_variance_score(y_true, y_pred)
1.0
>>> explained_variance_score(y_true, y_pred, force_finite=False)
nan
>>> y_true = [-2, -2, -2]
>>> y_pred = [-2, -2, -2 + 1e-8]
>>> explained_variance_score(y_true, y_pred)
0.0
>>> explained_variance_score(y_true, y_pred, force_finite=False)
-inf

3.4.35. 均值泊松、伽马和特威迪偏差#

mean_tweedie_deviance 函数计算带有 power 参数（\(p\) ）的 均值 Tweedie 偏差误差 。这是一种引出回归目标预测期望值的度量标准。

存在以下特殊情况：

如果 \(\hat{y}_i\) 是第 \(i\) 个样本的预测值，而 \(y_i\) 是对应的真实值，那么对于参数 \(p\) 的均值 Tweedie 偏差误差（D），在 \(n_{\text{samples}}\) 上估计为：

\[\begin{split}\text{D}(y, \hat{y}) = \frac{1}{n_\text{samples}} \sum_{i=0}^{n_\text{samples} - 1} \begin{cases} (y_i-\hat{y}_i)^2, & \text{for }p=0\text{ (Normal)}\\ 2(y_i \log(y_i/\hat{y}_i) + \hat{y}_i - y_i), & \text{for }p=1\text{ (Poisson)}\\ 2(\log(\hat{y}_i/y_i) + y_i/\hat{y}_i - 1), & \text{for }p=2\text{ (Gamma)}\\ 2\left(\frac{\max(y_i,0)^{2-p}}{(1-p)(2-p)}- \frac{y_i\,\hat{y}_i^{1-p}}{1-p}+\frac{\hat{y}_i^{2-p}}{2-p}\right), & \text{otherwise} \end{cases}\end{split}\]

Tweedie 偏差是一个次数为 2-power 的齐次函数。因此，对于 power=2 的 Gamma 分布，同时缩放 y_true 和 y_pred 对偏差没有影响。对于 power=1 的泊松分布，偏差呈线性缩放，而对于 power=0 的正态分布，偏差呈二次缩放。一般来说， power 越高，真实值与预测目标之间的极端偏差所占权重越小。

例如，让我们比较两个预测值 1.5 和 150，它们都比相应的真实值大 50%。

均方误差（ power=0 ）对第二个点的预测差异非常敏感，:

>>> from sklearn.metrics import mean_tweedie_deviance

>>> mean_tweedie_deviance([1.0], [1.5], power=0)
0.25
>>> mean_tweedie_deviance([100.], [150.], power=0)
2500.0

如果我们把 power 增加到 1，:

>>> mean_tweedie_deviance([1.0], [1.5], power=1)
0.18...
>>> mean_tweedie_deviance([100.], [150.], power=1)
18.9...

误差差异会减小。最后，通过设置 power=2

>>> mean_tweedie_deviance([1.0], [1.5], power=2)
0.14...
>>> mean_tweedie_deviance([100.], [150.], power=2)
0.14...

我们会得到相同的误差。因此，当 power=2 时，偏差仅对相对误差敏感。

3.4.36. Pinball 损失#

mean_pinball_loss 函数用于评估 分位数回归 模型的预测性能。

\[\text{pinball}(y, \hat{y}) = \frac{1}{n_{\text{samples}}} \sum_{i=0}^{n_{\text{samples}}-1} \alpha \max(y_i - \hat{y}_i, 0) + (1 - \alpha) \max(\hat{y}_i - y_i, 0)\]

当分位数参数 alpha 设置为 0.5 时，Pinball 损失的值相当于 mean_absolute_error 的一半。

以下是一个使用 mean_pinball_loss 函数的小示例:

>>> from sklearn.metrics import mean_pinball_loss
>>> y_true = [1, 2, 3]
>>> mean_pinball_loss(y_true, [0, 2, 3], alpha=0.1)
0.03...
>>> mean_pinball_loss(y_true, [1, 2, 4], alpha=0.1)
0.3...
>>> mean_pinball_loss(y_true, [0, 2, 3], alpha=0.9)
0.3...
>>> mean_pinball_loss(y_true, [1, 2, 4], alpha=0.9)
0.03...
>>> mean_pinball_loss(y_true, y_true, alpha=0.1)
0.0
>>> mean_pinball_loss(y_true, y_true, alpha=0.9)
0.0

可以通过特定选择的 alpha 构建评分器对象:

>>> from sklearn.metrics import make_scorer
>>> mean_pinball_loss_95p = make_scorer(mean_pinball_loss, alpha=0.95)

这样的评分器可以用于通过交叉验证评估分位数回归器的泛化性能：

还可以为超参数调优构建评分器对象。损失的符号必须切换，以确保更大意味着更好，如下面链接的示例中所解释的那样。

示例

  • 参见 梯度提升回归的预测区间 以了解使用分位数损失评估和调整分位数回归模型超参数的示例，该模型用于具有非对称噪声和异常值的数据。

3.4.37. D² 得分#

D² 得分计算解释的偏差比例。 它是 R² 的泛化，其中平方误差被泛化并替换为选择的偏差 \(\text{dev}(y, \hat{y})\) （例如，Tweedie、分位数或平均绝对误差）。D² 是一种 技能得分。其计算公式为

\[D^2(y, \hat{y}) = 1 - \frac{\text{dev}(y, \hat{y})}{\text{dev}(y, y_{\text{null}})} \,.\]

其中 \(y_{\text{null}}\) 是仅截距模型的最优预测 （例如，Tweedie 情况下的 y_true 均值，绝对误差的中位数，以及分位数损失的 alpha 分位数）。

与 R² 类似，最好的得分是 1.0，它可能是负的（因为模型可能任意更差）。一个总是预测 \(y_{\text{null}}\) 的常数模型，忽略输入特征，将得到 0.0 的 D² 得分。

#D² Tweedie 得分

d2_tweedie_score 函数实现了 D² 的特殊情况

其中 \(\text{dev}(y, \hat{y})\) 是 Tweedie 偏差，参见 均值泊松、伽马和特威迪偏差 。 它也被称为 D² Tweedie，并与 McFadden 的似然比指数相关。

参数 power 定义了 Tweedie 幂，如同 mean_tweedie_deviance 中所述。注意，对于 power=0 ， d2_tweedie_score 等于 r2_score （针对单一目标）。

可以通过以下方式构建具有特定 power 选择的成绩器对象:

>>> from sklearn.metrics import d2_tweedie_score, make_scorer
>>> d2_tweedie_score_15 = make_scorer(d2_tweedie_score, power=1.5)
#D² 分位数得分

d2_pinball_score 函数实现了带有分位数损失的 D² 的特殊情况，参见 Pinball 损失 ，即：

\[\text{dev}(y, \hat{y}) = \text{pinball}(y, \hat{y}).\]

参数 alpha 定义了分位数损失的斜率，如同 mean_pinball_loss (Pinball 损失 ) 中所述。它确定了分位数水平 alpha ，在该水平上分位数损失和 D² 都是最优的。注意，对于 alpha=0.5 （默认值），d2_pinball_score 等于 d2_absolute_error_score 。

可以通过以下方式构建具有特定 alpha 选择的成绩器对象:

>>> from sklearn.metrics import d2_pinball_score, make_scorer
>>> d2_pinball_score_08 = make_scorer(d2_pinball_score, alpha=0.8)
#D² 绝对误差得分

d2_absolute_error_score 函数实现了 平均绝对误差 的特殊情况：

\[\text{dev}(y, \hat{y}) = \text{MAE}(y, \hat{y}).\]

以下是 d2_absolute_error_score 函数的一些使用示例:

>>> from sklearn.metrics import d2_absolute_error_score
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> d2_absolute_error_score(y_true, y_pred)
0.764...
>>> y_true = [1, 2, 3]
>>> y_pred = [1, 2, 3]
>>> d2_absolute_error_score(y_true, y_pred)
1.0
>>> y_true = [1, 2, 3]

>>> y_pred = [2, 2, 2]
>>> d2_absolute_error_score(y_true, y_pred)
0.0

3.4.38. 回归模型的可视化评估#

在评估回归模型质量的方法中，scikit-learn 提供了 PredictionErrorDisplay 类。它允许以两种不同的方式直观地检查模型的预测误差。

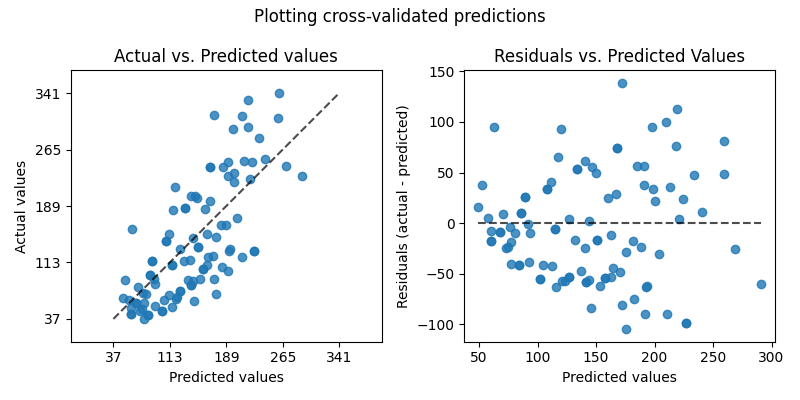
../_images/sphx_glr_plot_cv_predict_001.png

左边的图显示了实际值与预测值的关系。对于旨在预测 y 的（条件）期望的无噪声回归任务，一个完美的回归模型会在预测值等于实际值的对角线上显示数据点。离这条最佳线越远，模型的误差就越大。在更现实的设置中，存在不可减少的噪声，即并非 y 的所有变化都可以由 X 中的特征解释，那么最好的模型会导致数据点密集地排列在对角线周围。

请注意，上述情况仅在预测值是给定 X 的 y 的期望值时成立。这通常是回归模型的情况，这些模型最小化了均方误差目标函数或更一般地，对于任何“幂”参数值的最小化 均值 Tweedie 偏差 。

当绘制预测给定 X 的 y 的某个分位数的估计器的预测结果时，例如 QuantileRegressor 或任何其他最小化 pinball 损失 的模型，根据估计的分位数水平，一部分点预计会位于对角线的上方或下方。

总之，虽然直观易读，但这种图并不能真正告诉我们如何获得更好的模型。

右侧的图显示了残差（即实际值与预测值之间的差异）与预测值的关系。

这个图使得更容易可视化残差是否遵循

`同方差或异方差

<https://en.wikipedia.org/wiki/Homoscedasticity_and_heteroschedasticity>`_ 分布。

特别是，如果 y|X 的真实分布是泊松分布或伽马分布，预期最优模型的残差方差会随着 E[y|X] 的预测值增长（泊松分布为线性，伽马分布为二次）。

当拟合线性最小二乘回归模型（参见 LinearRegression 和 Ridge ），我们可以使用这个图来检查是否满足某些

`模型假设

<https://en.wikipedia.org/wiki/Ordinary_least_squares#Assumptions>`_ ， 特别是残差应该不相关，它们的期望值应该为零，并且它们的方差应该是常数（同方差性）。

如果不是这种情况，特别是如果残差图显示出某种香蕉形状的结构，这表明模型可能指定不当，非线性特征工程或切换到非线性回归模型可能是有用的。

请参阅下面的示例，了解如何利用这种显示进行模型评估。

示例

3.4.38.1. 聚类指标#

sklearn.metrics 模块实现了多个损失、评分和效用函数。更多信息请参见 clustering_evaluation 实例聚类部分，以及 双聚类评估 部分。

3.4.38.2. 虚拟估计器#

在进行监督学习时，一个简单的合理性检查包括将自己的估计器与简单的经验法则进行比较。DummyClassifier 实现了几种用于分类的简单策略：

  • stratified 通过尊重训练集的类别分布生成随机预测。

  • most_frequent 总是预测训练集中最频繁的标签。

  • prior 总是预测最大化类别先验的类别（类似于 most_frequent ），并且 predict_proba 返回类别先验。

  • uniform 均匀随机生成预测。

  • constant 总是预测用户提供的常量标签。这种方法的一个主要动机是在正类为少数类时进行 F1 评分。

请注意，使用所有这些策略时， predict 方法完全忽略了输入数据！

为了说明 DummyClassifier ，首先让我们创建一个不平衡的数据集:

>>> from sklearn.datasets import load_iris
>>> from sklearn.model_selection import train_test_split
>>> X, y = load_iris(return_X_y=True)
>>> y[y != 1] = -1
>>> X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

接下来，让我们比较 SVC 和 most_frequent 的准确率:

>>> from sklearn.dummy import DummyClassifier
>>> from sklearn.svm import SVC
>>> clf = SVC(kernel='linear', C=1).fit(X_train, y_train)
>>> clf.score(X_test, y_test)
0.63...
>>> clf = DummyClassifier(strategy='most_frequent', random_state=0)
>>> clf.fit(X_train, y_train)
DummyClassifier(random_state=0, strategy='most_frequent')
>>> clf.score(X_test, y_test)
0.57...

我们看到 SVC 并没有比虚拟分类器好多少。现在，让我们改变核函数:

 >>> clf = SVC(kernel='rbf', C=1).fit(X_train, y_train)
rst

>>> clf.score(X_test, y_test)
0.94...

我们看到准确率提升到了几乎100%。如果计算成本不是太高，建议使用交叉验证策略以获得更准确的准确率估计。更多信息请参见 交叉验证：评估估计器性能 部分。此外，如果你想在参数空间上进行优化，强烈建议使用适当的方法；详见 调整估计器的超参数 部分。

更一般地，当分类器的准确率过于接近随机时，这可能意味着某些地方出了问题：特征没有帮助，超参数没有正确调整，分类器受到类别不平衡的影响，等等。

DummyRegressor 也实现了四个简单的回归经验法则：

  • mean 总是预测训练目标的平均值。

  • median 总是预测训练目标的中位数。

  • quantile 总是预测用户提供的训练目标的分位数。

  • constant 总是预测用户提供的常数值。

在所有这些策略中， predict 方法完全忽略了输入数据。

On this page
Show Source