2.4. 双向聚类#

双向聚类算法同时对数据矩阵的行和列进行聚类。这些行和列的聚类被称为双向聚类。每个双向聚类确定原始数据矩阵的一个具有某些期望属性的子矩阵。

例如，给定一个形状为 (10, 10) 的矩阵，一个可能包含三行和两列的双向聚类会诱导出一个形状为 (3, 2) 的子矩阵:

>>> import numpy as np
>>> data = np.arange(100).reshape(10, 10)
>>> rows = np.array([0, 2, 3])[:, np.newaxis]
>>> columns = np.array([1, 2])
>>> data[rows, columns]
array([[ 1,  2],
       [21, 22],
       [31, 32]])

为了可视化目的，给定一个双向聚类，可以重新排列数据矩阵的行和列，使得双向聚类连续。

算法在定义双向聚类的方式上有所不同。一些常见的类型包括：

  • 常数值、常数行或常数列

  • 异常高或低的值

  • 低方差的子矩阵

  • 相关行或列

算法在行和列如何分配到双向聚类上也存在差异，这导致了不同的双向聚类结构。当行和列被分割成多个分区时，会出现块对角线或棋盘格结构。

如果每一行和每一列恰好属于一个双向聚类，那么重新排列数据矩阵的行和列会揭示对角线上的双向聚类。以下是一个这种结构的示例，其中双向聚类的平均值高于其他行和列：

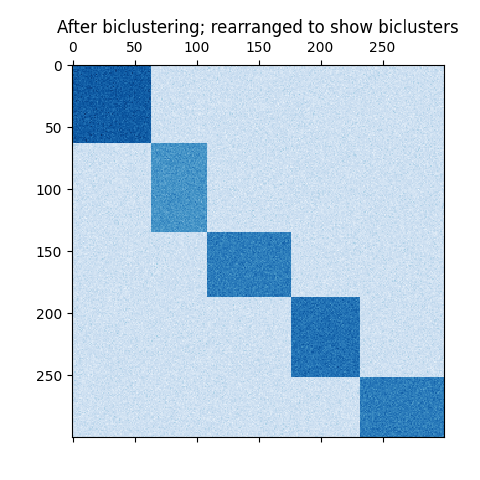
../_images/sphx_glr_plot_spectral_coclustering_003.png

通过行和列分区形成的双向聚类示例。#

在棋盘格情况下，每一行属于所有列聚类，每一列属于所有行聚类。以下是一个这种结构的示例： 结构中每个双聚类内的值的方差很小：

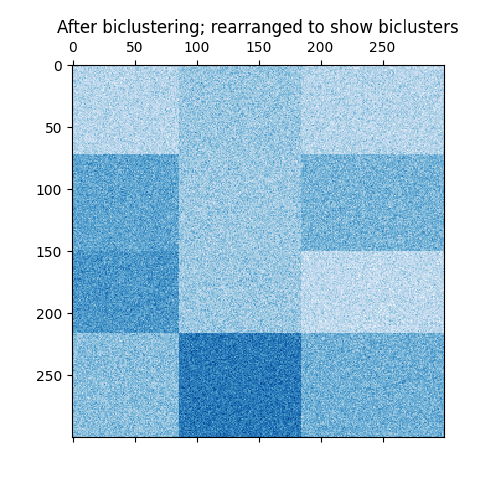
../_images/sphx_glr_plot_spectral_biclustering_003.png

棋盘格双聚类的示例。#

在拟合模型后，行和列的聚类成员关系可以在 rows_ 和 columns_ 属性中找到。 rows_[i] 是一个二进制向量，非零条目对应于属于双聚类 i 的行。类似地， columns_[i] 指示哪些列属于双聚类 i 。

一些模型还具有 row_labels_ 和 column_labels_ 属性。这些模型对行和列进行分区，例如在块对角线和棋盘格双聚类结构中。

Note

双聚类在不同领域有许多其他名称，包括协同聚类、双模聚类、双向聚类、块聚类、耦合双向聚类等。一些算法的名称，如谱协同聚类算法，反映了这些替代名称。

2.4.1. 谱协同聚类#

SpectralCoclustering 算法找到值高于相应其他行和列的双聚类。每行和每列恰好属于一个双聚类，因此重新排列行和列以使分区连续显示这些沿对角线的高值：

Note

该算法将输入数据矩阵视为二分图：矩阵的行和列对应于两组顶点，每个条目对应于行和列之间的边。该算法通过近似该图的归一化割来找到重子图。

2.4.1.1. 数学公式#

通过近似最优归一化割的解可以找到： 图的拉普拉斯矩阵的广义特征值分解。通常这意味着直接处理拉普拉斯矩阵。如果原始数据矩阵 \(A\) 的形状为 \(m \times n\) ，则对应二分图的拉普拉斯矩阵的形状为 \((m + n) \times (m + n)\) 。然而，在这种情况下，可以直接处理 \(A\) ，它更小且更高效。

输入矩阵 \(A\) 预处理如下：

\[A_n = R^{-1/2} A C^{-1/2}\]

其中 \(R\) 是对角矩阵，其第 \(i\) 个元素等于 \(\sum_{j} A_{ij}\) ，而 \(C\) 是对角矩阵，其第 \(j\) 个元素等于 \(\sum_{i} A_{ij}\) 。

奇异值分解 \(A_n = U \Sigma V^\top\) 提供了 \(A\) 的行和列的分区。左奇异向量的一个子集给出了行分区，右奇异向量的一个子集给出了列分区。

从第二个开始的 \(\ell = \lceil \log_2 k \rceil\) 个奇异向量提供了所需的分区信息。它们用于形成矩阵 \(Z\) ：

\[\begin{split}Z = \begin{bmatrix} R^{-1/2} U \\\\ C^{-1/2} V \end{bmatrix}\end{split}\]

其中 \(U\) 的列是 \(u_2, \dots, u_{\ell + 1}\) ，对于 \(V\) 也是如此。

然后使用 k-means 对 \(Z\) 的行进行聚类。前 n_rows 个标签提供了行分区，剩余的 n_columns 个标签提供了列分区。

示例

参考文献

  • Dhillon, Inderjit S, 2001. :doi:`Co-clustering documents and words using

二部谱图分区 <10.1145/502512.502550>`

2.4.2. 谱双聚类#

SpectralBiclustering 算法假设输入数据矩阵具有隐藏的棋盘结构。具有这种结构的矩阵的行和列可以被划分，使得在行簇和列簇的笛卡尔积中的任何双簇的条目近似恒定。例如，如果有两个行分区和三个列分区，每行将属于三个双簇，每列将属于两个双簇。

该算法对矩阵的行和列进行划分，使得相应的分块恒定棋盘矩阵对原始矩阵提供良好的近似。

2.4.2.1. 数学公式#

输入矩阵 \(A\) 首先被归一化以使棋盘模式更加明显。有三种可能的方法：

  1. 独立行和列归一化，如在谱协同聚类中。这种方法使行总和为常数，列总和为不同的常数。

  2. 双稳定化：重复行和列归一化直到收敛。这种方法使行和列总和为相同的常数。

  3. 对数归一化：计算数据矩阵的对数：\(L = \log A\) 。然后计算列均值 \(\overline{L_{i \cdot}}\) ，行均值 \(\overline{L_{\cdot j}}\) ，以及总体均值 \(\overline{L_{\cdot \cdot}}\) 的 \(L\) 。最终矩阵根据公式计算

\[K_{ij} = L_{ij} - \overline{L_{i \cdot}} - \overline{L_{\cdot j}} + \overline{L_{\cdot \cdot}}\]

归一化后，计算前几个奇异向量，就像在谱协同聚类算法中一样。

如果使用了对数归一化，所有奇异向量都是有意义的。然而，如果使用了独立归一化或双稳定化， 被使用的是第一奇异向量，\(u_1\) 和 \(v_1\) 。 这些被丢弃。从现在开始，“第一”奇异向量指的是 \(u_2 \dots u_{p+1}\) 和 \(v_2 \dots v_{p+1}\) ，除非在 对数归一化的情况下。

给定这些奇异向量，它们根据哪个可以 被最佳近似为分段常数向量进行排序。每个向量的 近似值使用一维k均值找到，并使用欧几里得距离进行评分。选择一些最好的左 和右奇异向量。接下来，数据被投影到 这个最好的奇异向量子集并进行聚类。

例如，如果计算了 \(p\) 个奇异向量，则 \(q\) 个最好的被找到，如所述，其中 \(q<p\) 。令 \(U\) 是列包含 \(q\) 个最好的左奇异向量的矩阵，同样地，\(V\) 是右奇异向量的矩阵。为了划分行， \(A\) 的行被投影到一个 \(q\) 维空间： \(A * V\) 。将这个 \(m \times q\) 矩阵的 \(m\) 行视为样本并使用k均值聚类得到行标签。 类似地，将列投影到 \(A^{\top} * U\) 并 聚类这个 \(n \times q\) 矩阵得到列标签。

示例

参考文献

2.4.3. 双聚类评估#

有两种评估双聚类结果的方法：内部和 外部。内部度量，如聚类稳定性，仅依赖于 数据和结果本身。目前scikit-learn中没有内部 双聚类度量。外部度量指的是

外部信息源，例如真实解。当处理真实数据时，真实解通常是未知的，但双聚类人工数据可能对精确评估算法非常有用，正是因为真实解是已知的。

要比较一组发现的双聚类与真实双聚类集合，需要两种相似性度量：单个双聚类的相似性度量，以及将这些个体相似性合并为一个总体得分的方法。

为了比较单个双聚类，已经使用了多种度量方法。目前，仅实现了Jaccard指数：

\[J(A, B) = \frac{|A \cap B|}{|A| + |B| - |A \cap B|}\]

其中 \(A\) 和 \(B\) 是双聚类，\(|A \cap B|\) 是它们交集中的元素数量。Jaccard指数在其最小值0时，当双聚类完全不重叠，而在其最大值1时，当它们完全相同时达到最大值。

已经开发了几种方法来比较两组双聚类。目前，仅提供了 consensus_score （Hochreiter等人，2010）：

  1. 使用Jaccard指数或类似度量计算每对双聚类的相似性，每对中一个来自每个集合。

  2. 以一对一的方式将一个集合中的双聚类分配给另一个集合中的双聚类，以最大化它们相似性的总和。这一步使用匈牙利算法执行。

  3. 最终的相似性总和除以较大集合的大小。

最小共识得分0发生在所有双聚类对完全不相似时。最大得分1发生在两组完全相同时。

参考文献

On this page
Show Source