1.6. 最近邻算法#

sklearn.neighbors 提供了无监督和有监督的基于邻居的学习方法的功能。无监督的最近邻算法是许多其他学习方法的基础，特别是流形学习和谱聚类。有监督的基于邻居的学习方法分为两种：用于具有离散标签的数据的 分类 和用于具有连续标签的数据的 `回归`_ 。

最近邻算法的基本原理是找到与新点距离最近的预定义数量的训练样本，并从这些样本中预测标签。样本数量可以是用户定义的常数（k-最近邻学习），也可以根据点的局部密度变化（基于半径的邻居学习）。一般来说，距离可以是任何度量标准：最常见的是标准欧几里得距离。基于邻居的方法被称为 非泛化 机器学习方法，因为它们只是简单地“记住”所有的训练数据（可能转换为快速索引结构，如 Ball Tree 或 KD Tree ）。

尽管简单，最近邻算法在大量的分类和回归问题中取得了成功，包括手写数字和卫星图像场景。作为一种非参数方法，它在决策边界非常不规则的分类情况下通常很成功。

sklearn.neighbors 中的类可以处理 NumPy 数组或 scipy.sparse 矩阵作为输入。对于密集矩阵，支持大量的可能距离度量。对于稀疏矩阵，支持任意 Minkowski 度量进行搜索。

有许多学习算法依赖于最近邻算法。 核心。一个例子是 核密度估计 ， 在 密度估计 部分讨论。

1.6.1. 无监督最近邻#

NearestNeighbors 实现了无监督的最近邻学习。 它作为一个统一的接口，提供了三种不同的最近邻算法：BallTree 、KDTree 和一个 基于 sklearn.metrics.pairwise 中的例程的暴力算法。 最近邻搜索算法的选择通过关键字 'algorithm' 控制，该关键字必须是

['auto', 'ball_tree', 'kd_tree', 'brute'] 之一。当传递默认值 'auto' 时，算法会尝试根据训练数据确定最佳方法。关于每种选项的优缺点的讨论，

请参见 `最近邻算法`_ 。

Warning

关于最近邻算法，如果两个邻居 \(k+1\) 和 \(k\) 具有相同的距离 但不同的标签，结果将取决于训练数据的顺序。

1.6.1.1. 寻找最近邻#

对于在两组数据之间寻找最近邻的简单任务，可以使用 sklearn.neighbors 中的无监督算法：

>>> from sklearn.neighbors import NearestNeighbors
>>> import numpy as np
>>> X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
>>> nbrs = NearestNeighbors(n_neighbors=2, algorithm='ball_tree').fit(X)
>>> distances, indices = nbrs.kneighbors(X)
>>> indices
array([[0, 1],
       [1, 0],
       [2, 1],
       [3, 4],
       [4, 3],
       [5, 4]]...)
>>> distances
array([[0.        , 1.        ],
       [0.        , 1.        ],
       [0.        , 1.41421356],
       [0.        , 1.        ],
       [0.        , 1.        ],

array([[0.        , 1.41421356],
       [1.41421356, 0.        ],
       [2.23606798, 1.41421356],
       [2.82842712, 2.23606798],
       [2.23606798, 2.82842712],
       [1.41421356, 2.23606798]])

因为查询集与训练集匹配，每个点的最近邻是点本身，距离为零。

也可以高效地生成一个稀疏图，显示相邻点之间的连接：

>>> nbrs.kneighbors_graph(X).toarray()
array([[1., 1., 0., 0., 0., 0.],
       [1., 1., 0., 0., 0., 0.],
       [0., 1., 1., 0., 0., 0.],
       [0., 0., 0., 1., 1., 0.],
       [0., 0., 0., 1., 1., 0.],
       [0., 0., 0., 0., 1., 1.]])

数据集的结构使得索引顺序相近的点在参数空间中也相近，导致了一个近似块对角矩阵的K近邻矩阵。这种稀疏图在各种情况下都很有用，这些情况利用了点之间的空间关系进行无监督学习：特别是，参见 Isomap 、LocallyLinearEmbedding 和 SpectralClustering 。

1.6.1.2. KDTree 和 BallTree 类#

或者，可以直接使用 KDTree 或 BallTree 类来查找最近邻。这是上面使用的 NearestNeighbors 类封装的功能。Ball Tree 和 KD Tree 具有相同的接口；我们在这里展示一个使用 KD Tree 的示例：

>>> from sklearn.neighbors import KDTree
>>> import numpy as np
>>> X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
>>> kdt = KDTree(X, leaf_size=30, metric='euclidean')
>>> kdt.query(X, k=2, return_distance=False)
array([[0, 1],
       [1, 0],
       [2, 1],
       [3, 4],
       [4, 3],
       [5, 4]]...)

有关最近邻搜索的更多选项，包括查询策略、距离度量等的指定，请参阅 KDTree 和 BallTree 类文档。对于距离度量的列表，请参阅 DistanceMetric 类。

有效度量指标的使用 KDTree.valid_metrics 和 BallTree.valid_metrics :

>>> from sklearn.neighbors import KDTree, BallTree
>>> KDTree.valid_metrics
['euclidean', 'l2', 'minkowski', 'p', 'manhattan', 'cityblock', 'l1', 'chebyshev', 'infinity']
>>> BallTree.valid_metrics
['euclidean', 'l2', 'minkowski', 'p', 'manhattan', 'cityblock', 'l1', 'chebyshev', 'infinity', 'seuclidean', 'mahalanobis', 'hamming', 'canberra', 'braycurtis', 'jaccard', 'dice', 'rogerstanimoto', 'russellrao', 'sokalmichener', 'sokalsneath', 'haversine', 'pyfunc']

1.6.2. 最近邻分类#

基于邻居的分类是一种 实例-based learning 或 非泛化学习 类型：它不尝试构建一个通用的内部模型，而是简单地存储训练数据的实例。分类是通过每个点的最近邻居的简单多数投票计算的：查询点被分配到其最近邻居中代表最多的数据类别。

scikit-learn 实现了两种不同的最近邻分类器：KNeighborsClassifier 实现了基于每个查询点的 \(k\) 个最近邻居的学习，其中 \(k\) 是用户指定的整数值。RadiusNeighborsClassifier 实现了基于每个训练点在固定半径 \(r\) 内的邻居数量的学习，其中 \(r\) 是用户指定的浮点数值。

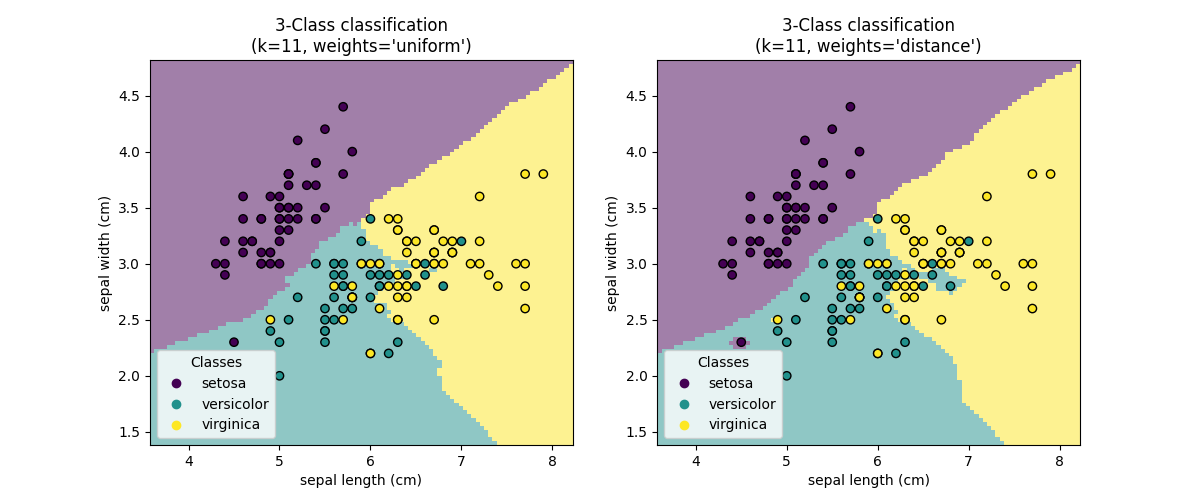
KNeighborsClassifier 中的 \(k\) -邻居分类是最常用的技术。值 \(k\) 的最佳选择高度依赖于数据：通常，较大的 \(k\) 会抑制噪声的影响，但会使分类边界不那么明显。

在数据不是均匀采样的情况下，RadiusNeighborsClassifier 中的基于半径的邻居分类可能是一个更好的选择。 用户指定一个固定半径 \(r\) ，使得在较稀疏的邻域中的点使用较少的最近邻进行分类。对于高维参数空间，由于所谓的“维度灾难”，这种方法变得不那么有效。

基本的最近邻分类使用均匀权重：即，分配给查询点的值是通过最近邻的简单多数投票计算的。在某些情况下，最好对邻居进行加权，使得更近的邻居对拟合的贡献更大。这可以通过 weights 关键字来实现。默认值 weights = 'uniform' 为每个邻居分配均匀权重。 weights = 'distance' 分配与查询点距离的倒数成比例的权重。或者，可以提供用户定义的距离函数来计算权重。

classification_1

示例

1.6.3. 最近邻回归#

基于邻居的回归可以用于数据标签是连续变量而不是离散变量的情况。分配给查询点的标签是基于其最近邻标签的平均值计算的。

scikit-learn 实现了两种不同的邻居回归器： KNeighborsRegressor 实现了基于每个查询点的 \(k\) 个最近邻的学习，其中 \(k\) 是用户指定的整数值。 RadiusNeighborsRegressor 实现了基于查询点在固定半径 \(r\) 内的邻居的学习，其中 \(r\) 是用户指定的浮点数值。 基本最近邻回归使用均匀权重：即，局部邻域中的每个点对查询点的分类贡献相同。在某些情况下，对点进行加权使得近点比远点对回归的贡献更大可能是有利的。这可以通过 weights 关键字来实现。默认值 weights = 'uniform' 为所有点分配相同的权重。 weights = 'distance' 分配与查询点距离的倒数成比例的权重。或者，可以提供用户定义的距离函数，该函数将用于计算权重。

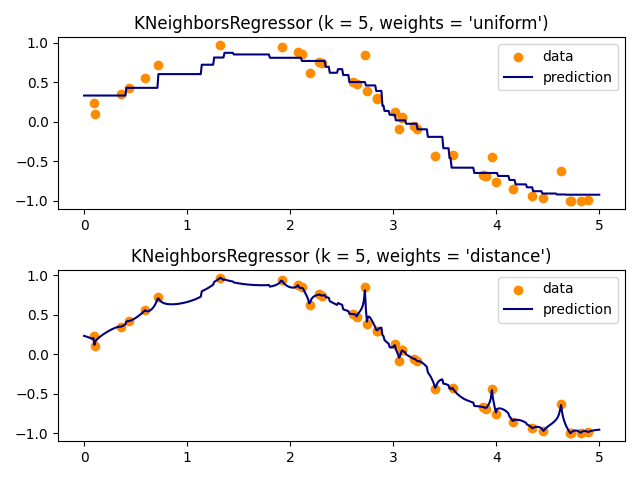
../_images/sphx_glr_plot_regression_001.png

多输出最近邻回归的使用在:ref:sphx_glr_auto_examples_miscellaneous_plot_multioutput_face_completion.py 中进行了演示。在这个例子中，输入X是面部上半部分的像素，输出Y是这些面部下半部分的像素。

../_images/sphx_glr_plot_multioutput_face_completion_001.png

示例

1.6.4. 最近邻算法#

1.6.4.1. 暴力搜索#

快速计算最近邻是机器学习中的一个活跃研究领域。最朴素的邻近搜索实现涉及在所有点对之间进行距离的暴力计算。 数据集：对于 \(N\) 个样本在 \(D\) 维空间中，这种方法的复杂度为 \(O[D N^2]\) 。 对于小数据样本，高效的暴力邻居搜索可以非常具有竞争力。 然而，随着样本数量 \(N\) 的增长，暴力方法很快变得不可行。 在 sklearn.neighbors 类中，暴力邻居搜索使用关键字 algorithm = 'brute' 指定，并使用 sklearn.metrics.pairwise 中可用的例程进行计算。

1.6.4.2. K-D 树#

为了解决暴力方法的计算效率问题，已经发明了各种基于树的数据结构。 一般来说，这些结构试图通过有效地编码样本的聚合距离信息来减少所需的距离计算数量。 基本思想是，如果点 \(A\) 与点 \(B\) 非常远，而点 \(B\) 与点 \(C\) 非常近，那么我们就知道点 \(A\) 和 \(C\) 非常远，而无需明确计算它们的距离。 通过这种方式，最近邻居搜索的计算成本可以降低到 \(O[D N \log(N)]\) 或更好。 这对于大 \(N\) 来说是一个显著的改进。

利用这种聚合信息的早期方法是 KD 树 数据结构（K 维树 的缩写），它将二维 四叉树 和三维 八叉树 推广到任意数量的维度。 KD 树是一种二叉树结构，它递归地沿着数据轴对参数空间进行分区，将其划分为嵌套的正交区域，数据点被归档到这些区域中。 KD 树的构建非常快：因为分区仅沿着数据轴进行，所以不需要计算 \(D\) 维距离。 一旦构建完成，查询点的最近邻居可以通过树的递归遍历来找到。 点可以通过仅进行 \(O[\log(N)]\) 次距离计算来确定。 尽管 KD 树方法对于低维度（\(D < 20\) ）的邻居搜索非常快速，但随着 \(D\) 变得非常大，它变得低效： 这是所谓的“维度灾难”的一种表现。 在 scikit-learn 中，使用关键字 algorithm = 'kd_tree' 指定 KD 树邻居搜索，并使用类 KDTree 进行计算。

#参考文献

1.6.4.3. Ball Tree#

为了解决 KD 树在高维度上的低效问题，开发了 ball tree 数据结构。KD 树沿着笛卡尔轴分割数据，而 ball tree 则在一系列嵌套的超球体中分割数据。这使得树的构建成本比 KD 树更高，但结果是一种在高度结构化的数据上非常高效的数据结构，即使在非常高维度的情况下也是如此。

Ball tree 递归地将数据分割成由质心 \(C\) 和半径 \(r\) 定义的节点，使得节点中的每个点都位于由 \(r\) 和 \(C\) 定义的超球体内。邻居搜索的候选点数量通过使用 三角不等式 来减少：

\[|x+y| \leq |x| + |y|\]

通过这种设置，测试点与质心之间的单次距离计算足以确定节点内所有点的距离的下界和上界。 由于 ball tree 节点的球形几何结构，它在高维度上可以胜过 KD-tree，尽管实际性能高度依赖于训练数据的结构。 在 scikit-learn 中，使用关键字 algorithm = 'ball_tree' 指定基于 ball tree 的邻居搜索。 并使用类 BallTree 进行计算。 或者，用户可以直接使用 BallTree 类。

#参考文献
#最近邻算法的选择

对于给定数据集，最优算法是一个复杂的选择，并且取决于多个因素：

  • 样本数量 \(N\) （即 n_samples ）和维度 \(D\) （即 n_features ）。

    • 暴力搜索 查询时间增长为 \(O[D N]\)

    • 球树 查询时间增长为大约 \(O[D \log(N)]\)

    • KD树 查询时间随 \(D\) 变化的方式很难精确描述。对于较小的 \(D\) （大约小于20）， 成本大约为 \(O[D\log(N)]\) ，KD树查询可以非常高效。 对于较大的 \(D\) ，成本增加到接近 \(O[DN]\) ， 由于树结构的额外开销可能导致查询比暴力搜索更慢。

    对于小数据集（\(N\) 小于30左右），\(\log(N)\) 与 \(N\) 相当， 暴力搜索算法可能比基于树的方法更高效。KDTree 和 BallTree 通过提供 叶大小 参数来解决这个问题：这控制了查询切换到暴力搜索的样本数量。 这使得两种算法在小 \(N\) 时接近暴力计算的效率。

  • 数据结构：数据的 固有维度 和/或 稀疏性。固有维度指的是数据所在的流形维度 \(d \le D\) ，可以是线性的 或者非线性地嵌入在参数空间中。稀疏性指的是数据填充参数空间的程度（这与“稀疏”矩阵中使用的概念不同。数据矩阵可能没有零项，但**结构**在这个意义上仍然可以是“稀疏”的）。

    • *暴力*查询时间不受数据结构的影响。

    • *球树*和*KD树*查询时间可以受到数据结构的极大影响。一般来说，具有较小内在维度的更稀疏数据会导致更快的查询时间。因为KD树的内部表示与参数轴对齐，所以对于任意结构的数据，它通常不会像球树那样显示出很大的改进。

    机器学习中使用的数据集往往非常有结构，非常适合基于树的查询。

  • 查询点请求的邻居数量 \(k\) 。

    • *暴力*查询时间在很大程度上不受 \(k\) 值的影响

    • *球树*和*KD树*查询时间会随着 \(k\) 的增加而变慢。这是由于两个效应：首先，更大的 \(k\) 导致需要搜索参数空间的更大部分。其次，使用 \(k > 1\) 需要在遍历树时内部排队结果。

    当 \(k\) 相对于 \(N\) 变大时，基于树的查询中修剪分支的能力会降低。在这种情况下，暴力查询可能更有效。

  • 查询点的数量。球树和KD树都需要一个构建阶段。当在许多查询中分摊时，这个构建成本变得可以忽略不计。然而，如果只执行少量查询，构建成本可能会占到总成本的很大一部分。如果只需要很少的查询点，暴力方法比基于树的方法更好。

目前， algorithm = 'auto' 在以下任一条件成立时会选择 'brute' ：

  • 输入数据是稀疏的

  • metric = 'precomputed'

  • \(D > 15\)

  • \(k >= N/2\)

  • effective_metric_ 不在 'kd_tree' 或 'ball_tree' 的 VALID_METRICS 列表中

否则，它会从 'kd_tree' 和 'ball_tree' 中选择第一个在其 VALID_METRICS 列表中包含 effective_metric_ 的方法。这一启发式选择基于以下假设：

  • 查询点的数量至少与训练点的数量相同

  • leaf_size 接近其默认值 30

  • 当 \(D > 15\) 时，数据的本征维度通常对于基于树的方法来说过高

#最近邻算法的有效度量

有关可用度量的列表，请参阅 DistanceMetric 类的文档以及 sklearn.metrics.pairwise.PAIRWISE_DISTANCE_FUNCTIONS 中列出的度量。请注意，“余弦”度量使用 cosine_distances 。

上述任何算法的有效度量列表可以通过使用它们的 valid_metric 属性获得。例如， KDTree 的有效度量可以通过以下方式生成：

>>> from sklearn.neighbors import KDTree
>>> print(sorted(KDTree.valid_metrics))
['chebyshev', 'cityblock', 'euclidean', 'infinity', 'l1', 'l2', 'manhattan', 'minkowski', 'p']

1.6.5. 最近质心分类器#

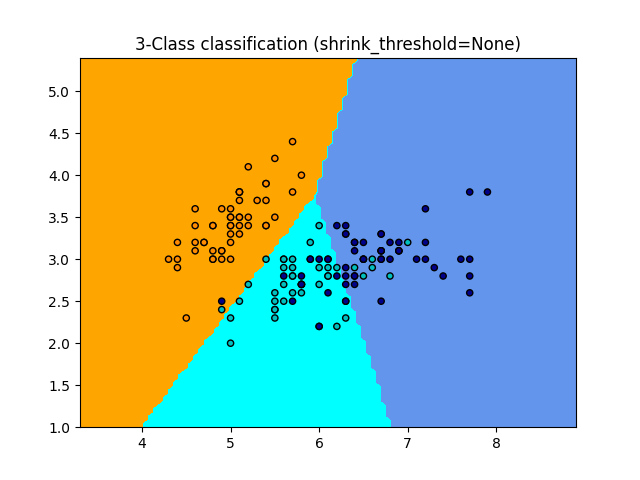
NearestCentroid 分类器是一种简单的算法，它通过其成员的质心来表示每个类别。实际上，这使得它类似于 KMeans 算法的标签更新阶段。它也没有参数需要选择，因此是一个很好的基线分类器。然而，它在非凸类别以及类别具有极大不同方差的情况下会受到影响，因为它假设所有维度具有相等的方差。有关不作此假设的更复杂方法，请参见线性判别分析（LinearDiscriminantAnalysis ）和二次判别分析（QuadraticDiscriminantAnalysis ）。默认 NearestCentroid 的使用很简单：

>>> from sklearn.neighbors import NearestCentroid
>>> import numpy as np
>>> X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
>>> y = np.array([1, 1, 1, 2, 2, 2])

>>> clf = NearestCentroid()
>>> clf.fit(X, y)
NearestCentroid()
>>> print(clf.predict([[-0.8, -1]]))
[1]

1.6.5.1. 最近质心分类器#

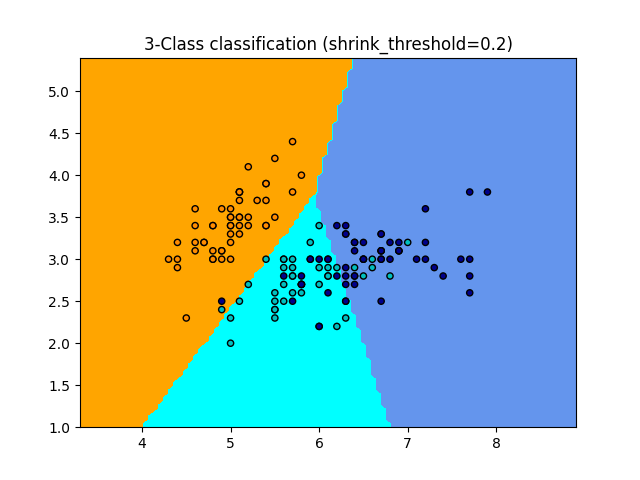
NearestCentroid 分类器有一个 shrink_threshold 参数， 它实现了最近收缩质心分类器。实际上，每个质心的每个特征值除以该特征的类内方差。 然后，特征值通过 shrink_threshold 减少。最值得注意的是，如果某个特征值越过零， 它将被设置为零。实际上，这会从影响分类中移除该特征。这对于移除噪声特征非常有用。

在下面的示例中，使用较小的收缩阈值将模型的准确性从 0.81 提高到 0.82。

nearest_centroid_1 nearest_centroid_2

示例

1.6.6. 最近邻变换器#

许多 scikit-learn 估计器依赖于最近邻：包括几种分类器和回归器，如 KNeighborsClassifier 和 KNeighborsRegressor ，以及一些聚类方法，如 DBSCAN 和 SpectralClustering ，还有一些流形嵌入方法，如 TSNE 和 Isomap 。

所有这些估计器都可以内部计算最近邻，但大多数

它们也接受预计算的最近邻 稀疏图 ， 如由 kneighbors_graph 和 radius_neighbors_graph 给出的那样。在模式

mode='connectivity' 下，这些函数返回所需的二进制邻接稀疏图，

例如在 SpectralClustering 中。 而在 mode='distance' 下，它们返回所需的距离稀疏图， 例如在 DBSCAN 中。为了在 scikit-learn 管道中包含这些函数，也可以使用相应的类 KNeighborsTransformer 和 RadiusNeighborsTransformer 。 这种稀疏图 API 的好处是多方面的。

首先，预计算的图可以多次重用，例如在改变估计器的参数时。 这可以由用户手动完成，或者使用 scikit-learn 管道的缓存属性：

>>> import tempfile
>>> from sklearn.manifold import Isomap
>>> from sklearn.neighbors import KNeighborsTransformer
>>> from sklearn.pipeline import make_pipeline
>>> from sklearn.datasets import make_regression
>>> cache_path = tempfile.gettempdir()  # 我们在这里使用一个临时文件夹
>>> X, _ = make_regression(n_samples=50, n_features=25, random_state=0)
>>> estimator = make_pipeline(
...     KNeighborsTransformer(mode='distance'),
...     Isomap(n_components=3, metric='precomputed'),
...     memory=cache_path)
>>> X_embedded = estimator.fit_transform(X)
>>> X_embedded.shape
(50, 3)

其次，预计算图可以对最近邻估计进行更精细的控制， 例如通过参数 n_jobs 启用多进程，这可能并非所有估计器都可用。

最后，预计算可以由自定义估计器执行，以使用不同的实现， 例如近似最近邻方法，或使用特殊数据类型的实现。预计算的邻接 稀疏图 需要按照以下格式进行格式化，如同在 radius_neighbors_graph 输出中一样：

  • 一个 CSR 矩阵（尽管 COO、CSC 或 LIL 也会被接受）。

  • 仅显式存储每个样本相对于训练数据的最近邻域。这应该包括那些与查询点距离为 0 的点，包括在计算训练数据与其自身之间的最近邻域时矩阵的对角线。

  • 每一行的 data 应该按距离递增的顺序存储（可选。未排序的数据将被稳定排序，增加计算开销）。

  • 数据中的所有值都应该是非负的。

  • 任何行中都不应该有重复的 indices （参见 scipy/scipy#5807）。

  • 如果传递预计算矩阵的算法使用 k 近邻（而不是半径邻域），则每行至少必须存储 k 个邻居（或 k+1 个，如以下注释所述）。

Note

当查询特定数量的邻居时（使用 KNeighborsTransformer ）， n_neighbors 的定义是模糊的，因为它可以包括每个训练点作为其自身的邻居，也可以排除它们。两种选择都不完美，因为包括它们会导致训练和测试期间非自身邻居的数量不同，而排除它们会导致 fit(X).transform(X) 和 fit_transform(X) 之间的差异，这与 scikit-learn API 相悖。 在 KNeighborsTransformer 中，我们使用包括每个训练点作为其自身邻居的定义来计算 n_neighbors 。然而，为了与其他使用另一种定义的估计器兼容，当 mode == 'distance' 时，将计算一个额外的邻居。为了与所有估计器最大化兼容性，一个安全的选择是在自定义最近邻估计器中始终包括一个额外的邻居，因为不必要的邻居将被后续估计器过滤。

示例

1.6.7. 邻域成分分析#

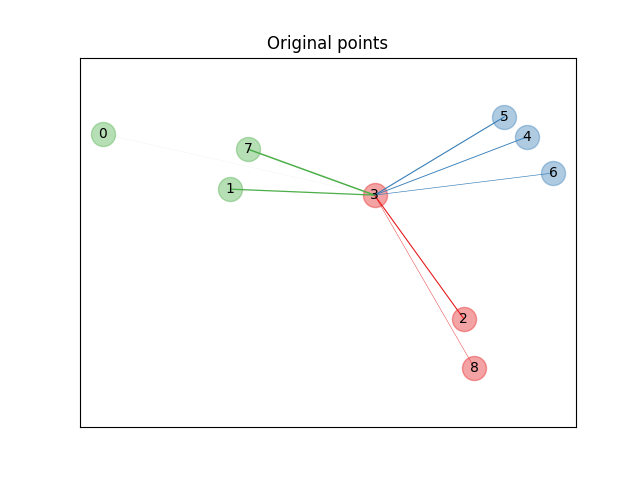
邻域成分分析（NCA，NeighborhoodComponentsAnalysis ）是一种距离度量学习算法，旨在提高最近邻分类的准确性，相比于标准欧氏距离。该算法直接最大化训练集上留一法 k-最近邻（KNN）分数的随机变体。它还可以学习数据的低维线性投影，用于数据可视化和快速分类。

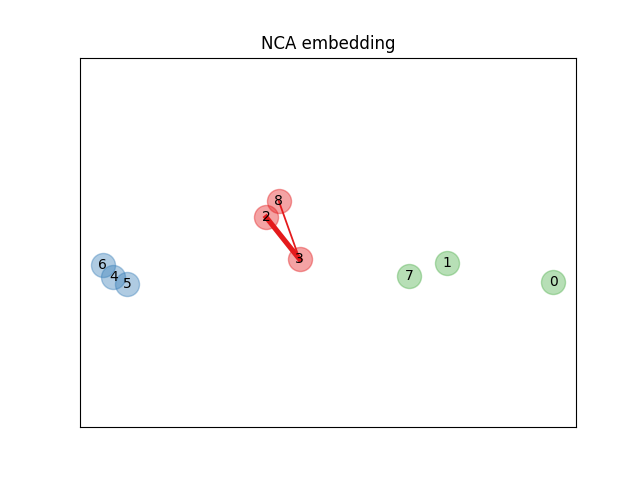
nca_illustration_1 nca_illustration_2

在上面的说明性图中，我们考虑了一些从随机生成的数据集中提取的点。我们关注点号3的随机KNN分类。样本3与另一个点之间的链接的粗细与其距离成正比，可以看作是随机最近邻预测规则分配给该点的相对权重（或概率）。 原始空间中，样本3有许多来自不同类别的随机邻居，因此正确的类别可能性不大。然而，在NCA学习到的投影空间中，唯一具有不可忽略权重的随机邻居来自与样本3相同的类别，确保了后者将被很好地分类。更多细节请参见 数学公式 。

1.6.7.1. 分类#

结合最近邻分类器（KNeighborsClassifier ），NCA在分类方面具有吸引力，因为它可以自然地处理多类别问题，而不会增加模型大小，并且不会引入需要用户微调的额外参数。

实践证明，NCA分类在不同大小和难度的数据集上表现良好。与线性判别分析等相关的其他方法相比，NCA不对类别分布做出任何假设。最近邻分类可以自然地产生高度不规则的决策边界。

要使用此模型进行分类，需要将学习最优变换的 NeighborhoodComponentsAnalysis 实例与在投影空间中执行分类的 KNeighborsClassifier 实例结合起来。以下是使用两个类别的示例：

>>> from sklearn.neighbors import (NeighborhoodComponentsAnalysis,
... KNeighborsClassifier)
>>> from sklearn.datasets import load_iris
>>> from sklearn.model_selection import train_test_split
>>> from sklearn.pipeline import Pipeline
>>> X, y = load_iris(return_X_y=True)
>>> X_train, X_test, y_train, y_test = train_test_split(X, y,
... stratify=y, test_size=0.7, random_state=42)
>>> nca = NeighborhoodComponentsAnalysis(random_state=42)
>>> knn = KNeighborsClassifier(n_neighbors=3)
>>> nca_pipe = Pipeline([('nca', nca), ('knn', knn)])
>>> nca_pipe.fit(X_train, y_train)

Pipeline(…) >>> print(nca_pipe.score(X_test, y_test)) 0.96190476…

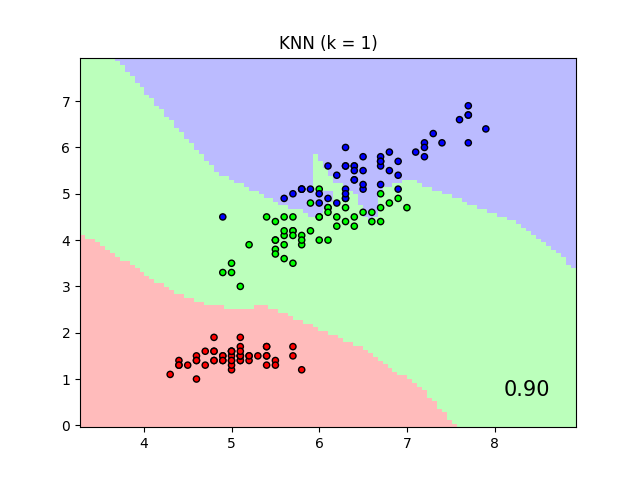
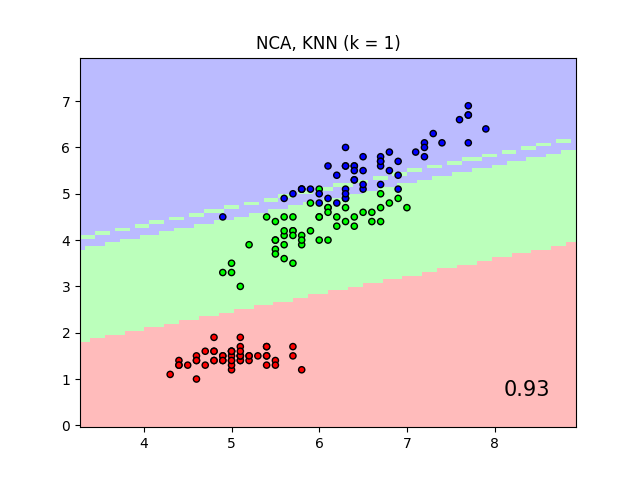
nca_classification_1 nca_classification_2

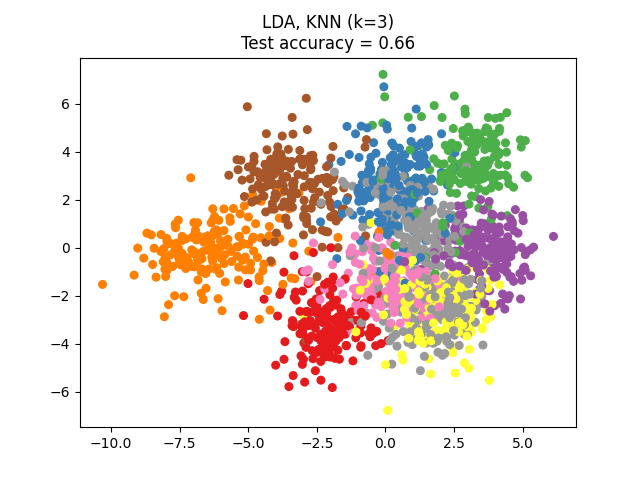
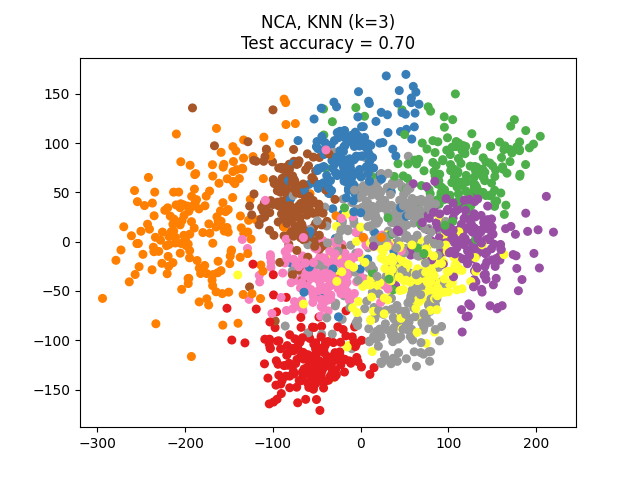
该图显示了在鸢尾花数据集上，仅使用两个特征进行可视化目的的训练和评分时，最近邻分类和邻域成分分析分类的决策边界。

1.6.7.2. 降维#

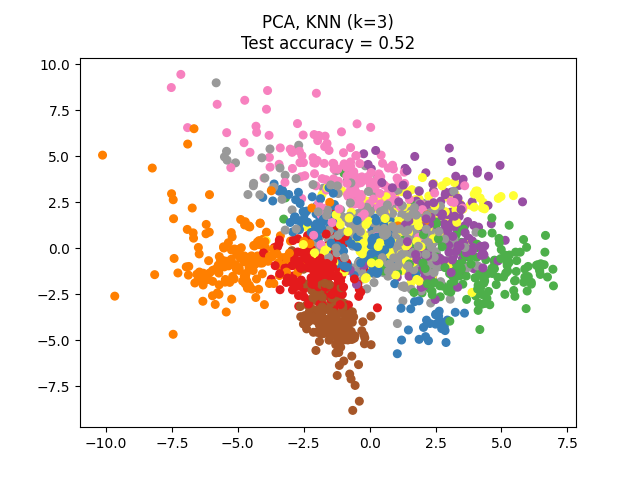
NCA 可以用于执行监督降维。输入数据被投影到一个由最小化 NCA 目标的方向组成的线性子空间上。期望的维度可以通过参数 n_components 设置。例如，下图展示了在 Digits 数据集上，主成分分析（PCA ）、线性判别分析（LinearDiscriminantAnalysis ）和邻域成分分析（NeighborhoodComponentsAnalysis ）的降维比较，该数据集大小为 \(n_{samples} = 1797\) 和 \(n_{features} = 64\) 。数据集被分成大小相等的训练集和测试集，然后进行标准化。为了评估，在每种方法找到的二维投影点上计算 3-最近邻分类准确率。每个数据样本属于 10 个类别之一。

nca_dim_reduction_1 nca_dim_reduction_2 nca_dim_reduction_3

示例

1.6.7.3. 数学公式#

NCA的目标是学习一个最优的线性变换矩阵，大小为 (n_components, n_features) ，该矩阵最大化所有样本 \(i\) 的正确分类概率 \(p_i\) 的总和，即：

\[\underset{L}{\arg\max} \sum\limits_{i=0}^{N - 1} p_{i}\]

其中 \(N\) = n_samples ，\(p_i\) 是样本 \(i\) 在学习的嵌入空间中根据随机最近邻规则正确分类的概率：

\[p_{i}=\sum\limits_{j \in C_i}{p_{i j}}\]

其中 \(C_i\) 是与样本 \(i\) 同类的点的集合，\(p_{i j}\) 是嵌入空间中欧几里得距离的 softmax：

\[p_{i j} = \frac{\exp(-||L x_i - L x_j||^2)}{\sum\limits_{k \ne i} {\exp{-(||L x_i - L x_k||^2)}}} , \quad p_{i i} = 0\]
#马哈拉诺比斯距离

NCA 可以看作是学习一个（平方）马哈拉诺比斯距离度量：

\[|| L(x_i - x_j)||^2 = (x_i - x_j)^TM(x_i - x_j),\]

其中 \(M = L^T L\) 是一个大小为 (n_features, n_features) 的对称半正定矩阵。

1.6.7.4. 实现#

此实现遵循原始论文[1]_中的解释。对于优化方法，目前使用scipy的L-BFGS-B，在每次迭代中进行完整的梯度计算，以避免调整学习率和提供稳定的训练。

请参阅下面的示例和:meth:NeighborhoodComponentsAnalysis.fit 的文档字符串以获取更多信息。

1.6.7.5. 复杂度#

1.6.7.5.1. 训练#

NCA存储一个成对距离矩阵，占用 n_samples ** 2 的内存。时间复杂度取决于优化算法执行的迭代次数。然而，可以使用参数 max_iter 设置最大迭代次数。对于每次迭代，时间复杂度为 O(n_components x n_samples x min(n_samples, n_features)) 。

1.6.7.5.2. 转换#

这里的 transform 操作返回:math:LX^T ，因此其时间复杂度等于 n_components * n_features * n_samples_test 。该操作没有增加空间复杂度。

参考文献

On this page
Show Source