1.5. 随机梯度下降#

随机梯度下降 (SGD) 是一种简单但非常高效的方法，用于在凸损失函数下拟合线性分类器和回归器，例如（线性） 支持向量机 和 逻辑回归 。尽管 SGD 在机器学习社区中已经存在很长时间，但最近在大规模学习的背景下受到了相当多的关注。

SGD 已成功应用于大规模和稀疏的机器学习问题，这些问题在文本分类和自然语言处理中经常遇到。鉴于数据是稀疏的，该模块中的分类器很容易扩展到具有超过 10^5 个训练样本和超过 10^5 个特征的问题。

严格来说，SGD 仅仅是一种优化技术，并不对应于特定的机器学习模型家族。它只是一种训练模型的 方式。通常，SGDClassifier 或 SGDRegressor 的实例在 scikit-learn API 中会有一个等效的估计器，可能使用不同的优化技术。例如，使用 SGDClassifier(loss='log_loss') 会得到逻辑回归，即一个与 LogisticRegression 等效的模型，该模型通过 SGD 而不是通过 LogisticRegression 中的其他求解器进行拟合。类似地， SGDRegressor(loss='squared_error', penalty='l2') 和 Ridge 通过不同的方式解决相同的优化问题。

随机梯度下降的优点包括：

  • 效率。

  • 易于实现（有很多代码调整的机会）。

随机梯度下降的缺点包括： + SGD 需要多个超参数，例如正则化参数和迭代次数。

  • SGD 对特征缩放敏感。

Warning

在拟合模型之前，请确保对训练数据进行排列（打乱），或者使用 shuffle=True 在每次迭代后进行打乱（默认使用）。此外，理想情况下，应使用例如 make_pipeline(StandardScaler(), SGDClassifier()) （参见 管道 ）对特征进行标准化。

1.5.1. 分类#

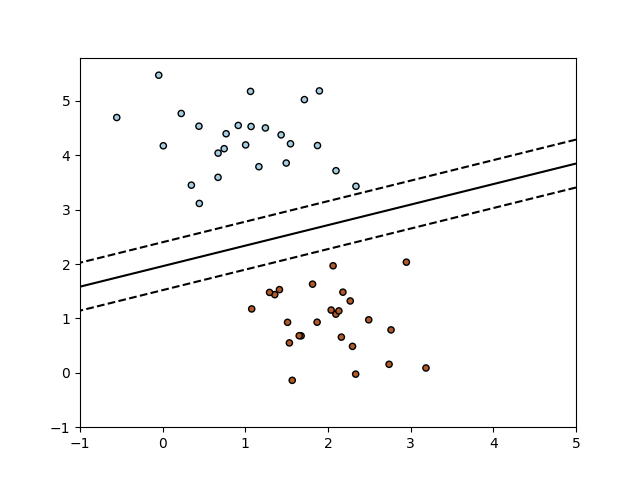
类 SGDClassifier 实现了一个简单的随机梯度下降学习程序，支持不同的损失函数和分类的惩罚。下面是一个使用铰链损失训练的 SGDClassifier 的决策边界，相当于一个线性 SVM。

../_images/sphx_glr_plot_sgd_separating_hyperplane_001.png

与其他分类器一样，SGD 需要拟合两个数组：一个形状为 (n_samples, n_features) 的数组 X 保存训练样本，以及一个形状为 (n_samples,) 的数组 y 保存训练样本的目标值（类别标签）:

>>> from sklearn.linear_model import SGDClassifier
>>> X = [[0., 0.], [1., 1.]]
>>> y = [0, 1]
>>> clf = SGDClassifier(loss="hinge", penalty="l2", max_iter=5)
>>> clf.fit(X, y)
SGDClassifier(max_iter=5)

拟合后，模型可以用于预测新值:

>>> clf.predict([[2., 2.]])
array([1])

SGD 将一个线性模型拟合到训练数据。 coef_ 属性保存模型参数:

   >>> clf.coef_
   array([[9.9..., 9.9...]])

``intercept_`` 属性保存截距（即偏移或偏差）::

   >>> clf.intercept_
   array([-9.9...])

模型是否应使用截距，即有偏超平面，由参数 fit_intercept 控制。 超平面到样本的有符号距离（计算为系数与输入样本的点积，加上截距）由 :meth :SGDClassifier.decision_function 给出:

>>> clf.decision_function([[2., 2.]])
array([29.6...])

具体的损失函数可以通过 loss 参数设置。SGDClassifier 支持以下损失函数：

  • loss="hinge" ：（软间隔）线性支持向量机，

  • loss="modified_huber" ：平滑的合页损失，

  • loss="log_loss" ：逻辑回归，

  • 以及所有下面的回归损失。在这种情况下，目标被编码为 -1 或 1，问题被视为回归问题。预测的类别对应于预测目标的符号。

请参阅下面的 数学部分 以获取公式。 前两个损失函数是惰性的，它们仅在示例违反了边界约束时更新模型参数，这使得训练非常高效，并且可能导致更稀疏的模型（即具有更多零系数的模型），即使在使用了 L2 惩罚的情况下也是如此。

使用 loss="log_loss" 或 loss="modified_huber" 可以启用 predict_proba 方法，该方法为每个样本 \(x\) 提供概率估计向量 \(P(y|x)\)

>>> clf = SGDClassifier(loss="log_loss", max_iter=5).fit(X, y)
>>> clf.predict_proba([[1., 1.]]) 
array([[0.00..., 0.99...]])

具体的惩罚可以通过 penalty 参数设置。SGD 支持以下惩罚：

  • penalty="l2" ：对 coef_ 的 L2 范数惩罚。

  • penalty="l1" ：对 coef_ 的 L1 范数惩罚。

  • penalty="elasticnet" ：L2 和 L1 的凸组合； (1 - l1_ratio) * L2 + l1_ratio * L1 。

默认设置是 penalty="l2" 。L1 惩罚导致稀疏解，驱动大多数系数为零。弹性网络 [11] 解决了在存在高度相关特征时 L1 惩罚的一些缺陷。 属性。参数 l1_ratio 控制 L1 和 L2 惩罚的凸组合。

SGDClassifier 通过在“一对多”（OVA）方案中结合多个二元分类器来支持多类分类。对于每个 \(K\) 类，学习一个二元分类器，该分类器区分该类和所有其他 \(K-1\) 类。在测试时，我们计算每个分类器的置信度分数（即到超平面的带符号距离），并选择具有最高置信度的类别。下图说明了鸢尾花数据集上的 OVA 方法。虚线表示三个 OVA 分类器；背景颜色显示由这三个分类器引起的决策表面。

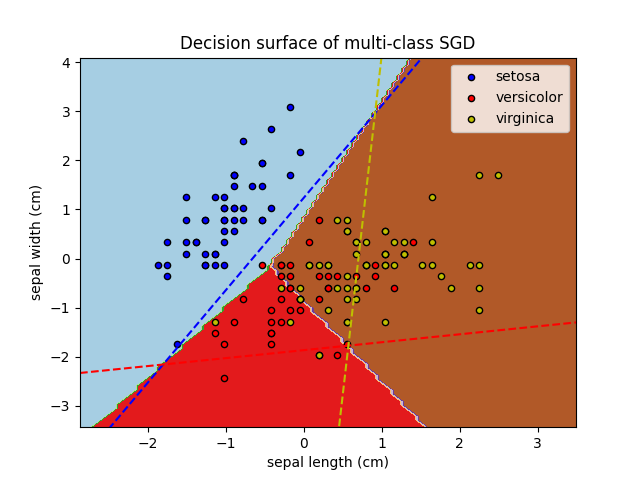
../_images/sphx_glr_plot_sgd_iris_001.png

在多类分类的情况下， coef_ 是一个形状为 (n_classes, n_features) 的二维数组，而 intercept_ 是一个形状为 (n_classes,) 的一维数组。 coef_ 的第 i 行保存了第 i 类的 OVA 分类器的权重向量；类按升序索引（参见属性 classes_ ）。请注意，原则上，由于它们允许创建概率模型， loss="log_loss" 和 loss="modified_huber" 更适合一对多分类。

SGDClassifier 通过拟合参数 class_weight 和 sample_weight 支持加权类和加权实例。请参阅下面的示例和 SGDClassifier.fit 的文档字符串以获取更多信息。

SGDClassifier 支持平均随机梯度下降（ASGD）[#4]_。可以通过设置 average=True 来启用平均。ASGD 执行与常规 SGD 相同的更新（参见 数学公式 ），但不是使用系数的最后一个值作为 coef_ 属性（即值 of the last update), coef_ is set instead to the average value of the coefficients across all updates. The same is done for the intercept_ attribute. When using ASGD the learning rate can be larger and even constant, leading on some datasets to a speed up in training time.

对于分类问题，使用逻辑损失函数时，还有一种带有平均策略的SGD变体，即随机平均梯度（Stochastic Average Gradient, SAG）算法，该算法作为求解器在 LogisticRegression 中可用。

示例

1.5.2. 回归#

类 SGDRegressor 实现了一个简单的随机梯度下降学习程序，支持不同的损失函数和惩罚项来拟合线性回归模型。SGDRegressor 非常适合训练样本数量庞大的回归问题（> 10,000），对于其他问题，我们推荐使用 Ridge 、Lasso 或 ElasticNet 。

具体的损失函数可以通过 loss 参数设置。SGDRegressor 支持以下损失函数：

  • loss="squared_error" : 普通最小二乘法，

  • loss="huber" : 用于稳健回归的Huber损失，

  • loss="epsilon_insensitive" : 线性支持向量回归。

请参阅下面的 数学部分 以获取公式。Huber和epsilon-insensitive损失函数可用于稳健回归。不敏感区域的宽度需要通过参数 epsilon 指定。该参数取决于目标变量的尺度。

penalty 参数决定了要使用的正则化方法（参见分类部分上面的描述）。

SGDRegressor 也支持平均 SGD [#4]_（再次参见分类部分上面的描述）。

对于使用平方损失和 l2 惩罚的回归，另一种带有平均策略的 SGD 变体是随机平均梯度（SAG）算法，可作为 Ridge 中的求解器使用。

1.5.3. 在线一类 SVM#

类 sklearn.linear_model.SGDOneClassSVM 实现了使用随机梯度下降的在线线性一类 SVM。结合核近似技术，sklearn.linear_model.SGDOneClassSVM 可以用来近似实现 sklearn.svm.OneClassSVM 中的核化一类 SVM 的解，其线性复杂度与样本数量成线性关系。请注意，核化一类 SVM 的复杂度在最优情况下也是样本数量的二次方。因此，sklearn.linear_model.SGDOneClassSVM 非常适合具有大量训练样本（> 10,000）的数据集，SGD 变体可以快几个数量级。

#数学细节

其实现基于随机梯度下降的实现。实际上，一类 SVM 的原始优化问题如下：

\[\begin{split}\begin{aligned} \min_{w, \rho, \xi} & \quad \frac{1}{2}\Vert w \Vert^2 - \rho + \frac{1}{\nu n} \sum_{i=1}^n \xi_i \\ \text{s.t.} & \quad \langle w, x_i \rangle \geq \rho - \xi_i \quad 1 \leq i \leq n \\ & \quad \xi_i \geq 0 \quad 1 \leq i \leq n \end{aligned}\end{split}\]

其中 \(\nu \in (0, 1]\) 是用户指定的参数，用于控制异常值和支持向量的比例。去掉松弛变量 \(\xi_i\) ，这个问题等价于

\[\min_{w, \rho} \frac{1}{2}\Vert w \Vert^2 - \rho + \frac{1}{\nu n} \sum_{i=1}^n \max(0, \rho - \langle w, x_i \rangle) \, .\]

乘以常数 \(\nu\) 并引入截距 \(b = 1 - \rho\) ，我们得到以下等价的优化问题

\[\min_{w, b} \frac{\nu}{2}\Vert w \Vert^2 + b\nu + \frac{1}{n} \sum_{i=1}^n \max(0, 1 - (\langle w, x_i \rangle + b)) \, .\]

这与第 数学公式 节中研究的优化问题类似，其中 \(y_i = 1, 1 \leq i \leq n\) 且 \(\alpha = \nu/2\) ，\(L\) 为合页损失函数，\(R\) 为 L2 范数。我们只需在优化循环中添加项 \(b\nu\) 。

与 SGDClassifier 和 SGDRegressor 一样，SGDOneClassSVM 支持平均 SGD。可以通过设置 average=True 来启用平均。

Note

稀疏实现与密集实现产生的结果略有不同，这是由于截距的学习率缩小了。详情请参见 实现细节 。

内置支持以 scipy.sparse 支持的任何矩阵格式给出的稀疏数据。然而，为了最大限度地提高效率，请使用 scipy.sparse.csr_matrix 中定义的 CSR 矩阵格式。

示例

SGD 的主要优势是其效率，基本上与训练样本的数量成线性关系。如果 X 是一个大小为 (n, p) 的矩阵，训练的成本为 \(O(k n \bar p)\) ，其中 k 是迭代次数（epochs），\(\bar p\) 是每个样本的非零属性的平均数量。

最近的理论结果表明，为了达到某种期望的优化精度，运行时间并不会随着训练集大小的增加而增加。

1.5.4. 停止准则#

类 SGDClassifier 和 SGDRegressor 提供了两种在达到给定收敛水平时停止算法的准则：

  • 当 early_stopping=True 时，输入数据被分为训练集和验证集。模型随后在训练集上进行拟合，停止准则是基于在验证集上计算的预测得分（使用 score 方法）。验证集的大小可以通过参数 validation_fraction 进行调整。

  • 当 early_stopping=False 时，模型在整个输入数据上进行拟合，停止准则是基于在训练数据上计算的目标函数。

在这两种情况下，准则每轮评估一次，当准则连续 n_iter_no_change 次没有改进时，算法停止。改进是通过绝对容差 tol 进行评估的，并且算法在达到最大迭代次数 max_iter 后无论如何都会停止。

1.5.5. 实用建议#

  • 随机梯度下降对特征缩放敏感，因此强烈建议对数据进行缩放。例如，将输入向量 X 中的每个属性缩放到 [0,1] 或 [-1,+1]，或者标准化使其均值为 0 且方差为 1。请注意，必须对测试向量应用相同的缩放以获得有意义的结果。这可以通过使用 StandardScaler 轻松实现:

    from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)  # 不要作弊 - 仅在训练数据上进行拟合
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)  # 对测试数据应用相同的变换

# 或者更好的是：使用管道！

from sklearn.pipeline import make_pipeline
est = make_pipeline(StandardScaler(), SGDClassifier())
est.fit(X_train)
est.predict(X_test)

    如果你的属性具有内在尺度（例如词频或指示特征），则不需要进行缩放。

  • 寻找一个合理的正则化项 \(\alpha\) 最好通过自动超参数搜索来完成，例如 GridSearchCV 或 RandomizedSearchCV ，通常在范围 10.0**-np.arange(1,7) 内进行。

  • 根据经验，我们发现 SGD 在观察大约 10^6 个训练样本后收敛。因此，迭代次数的合理初步猜测是 max_iter = np.ceil(10**6 / n) ， 其中 n 是训练集的大小。

  • 如果你将 SGD 应用于使用 PCA 提取的特征，我们发现通常明智的做法是通过某个常数 c 缩放特征值，使得训练数据的平均 L2 范数等于 1。

  • 我们发现，Averaged SGD 在具有更多特征和更高 eta0 的情况下效果最佳。

参考文献

  • “Efficient BackProp” Y. LeCun, L. Bottou, G. Orr, K. Müller - 在 Neural Networks: Tricks of the Trade 1998 中。

1.5.6. 数学公式#

我们在这里描述 SGD 过程的数学细节。有关收敛率的良好概述可以在 [12] 中找到。

给定一组训练样本 \((x_1, y_1), \ldots, (x_n, y_n)\) ，其中 \(x_i \in \mathbf{R}^m\) 和 \(y_i \in \mathcal{R}\) （对于分类，\(y_i \in {-1, 1}\) ），我们的目标是学习一个线性评分函数 \(f(x) = w^T x + b\) ，其中模型参数 \(w \in \mathbf{R}^m\) 和截距 \(b \in \mathbf{R}\) 。为了进行二元分类预测，我们只需查看 \(f(x)\) 的符号。为了找到模型参数，

参数，我们最小化由以下公式给出的正则化训练误差：

\[E(w,b) = \frac{1}{n}\sum_{i=1}^{n} L(y_i, f(x_i)) + \alpha R(w)\]

其中 \(L\) 是一个衡量模型（不）拟合程度的损失函数， \(R\) 是一个正则化项（又称惩罚项），用于惩罚模型复杂度； \(\alpha > 0\) 是一个非负超参数，用于控制正则化强度。

#损失函数详细信息

不同的 \(L\) 选择对应不同的分类器或回归器：

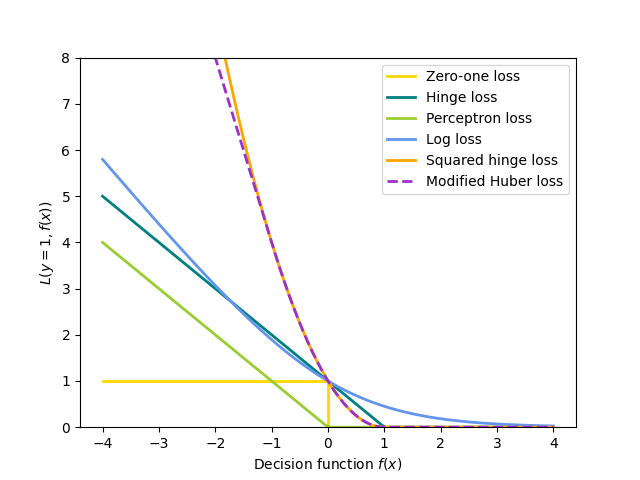
  • Hinge（软间隔）：等价于支持向量分类。 \(L(y_i, f(x_i)) = \max(0, 1 - y_i f(x_i))\) 。

  • 感知机： \(L(y_i, f(x_i)) = \max(0, - y_i f(x_i))\) 。

  • 改进的 Huber： \(L(y_i, f(x_i)) = \max(0, 1 - y_i f(x_i))^2\) 如果 \(y_i f(x_i) > -1\) ，否则 \(L(y_i, f(x_i)) = -4 y_i f(x_i)\) 。

  • 对数损失：等价于逻辑回归。 \(L(y_i, f(x_i)) = \log(1 + \exp (-y_i f(x_i)))\) 。

  • 平方误差：线性回归（根据 \(R\) 是 Ridge 或 Lasso）。 \(L(y_i, f(x_i)) = \frac{1}{2}(y_i - f(x_i))^2\) 。

  • Huber：对异常值比最小二乘法更不敏感。当 \(|y_i - f(x_i)| \leq \varepsilon\) 时，等价于最小二乘法， 否则 \(L(y_i, f(x_i)) = \varepsilon |y_i - f(x_i)| - \frac{1}{2} \varepsilon^2\) 。

  • Epsilon-Insensitive：（软间隔）等价于支持向量回归。 \(L(y_i, f(x_i)) = \max(0, |y_i - f(x_i)| - \varepsilon)\) 。

上述所有损失函数都可以视为误分类错误（零一损失）的上界，如下图所示。

../_images/sphx_glr_plot_sgd_loss_functions_001.png

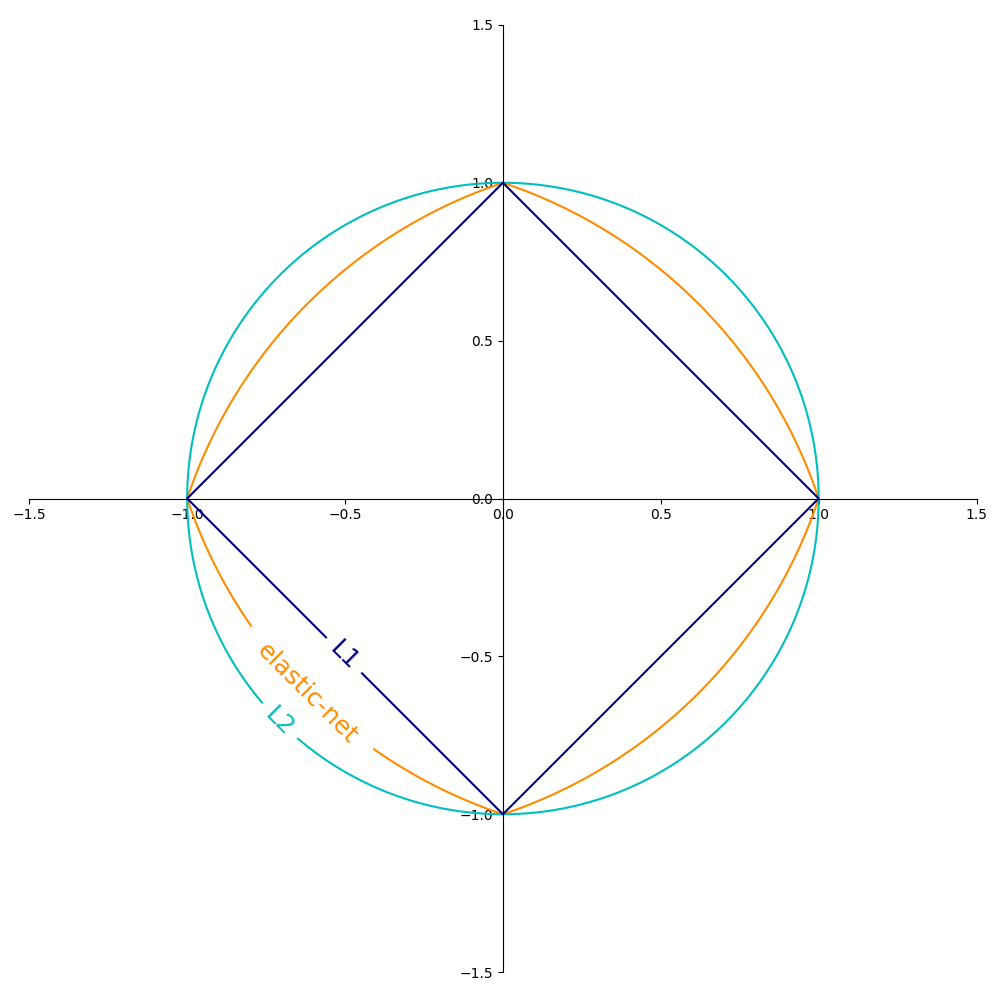
正则化项 \(R\) （即 惩罚 参数）的常见选择包括： - L2范数: \(R(w) := \frac{1}{2} \sum_{j=1}^{m} w_j^2 = ||w||_2^2\) , - L1范数: \(R(w) := \sum_{j=1}^{m} |w_j|\) , 这会导致稀疏解。 - 弹性网络: :math:`R(w) := frac{rho}{2} sum_{j=1}^{n} w_j^2 +

(1-rho) sum_{j=1}^{m} |w_j|` , 是L2和L1的凸组合，其中 \(\rho\) 由 1 - l1_ratio 给出。

下图显示了在二维参数空间（\(m=2\) ）中，当 \(R(w) = 1\) 时不同正则化项的等高线。

../_images/sphx_glr_plot_sgd_penalties_001.png

1.5.6.1. SGD#

随机梯度下降是一种用于无约束优化问题的优化方法。与批量梯度下降相比，SGD通过一次考虑一个训练样本来近似 \(E(w,b)\) 的真实梯度。

类 SGDClassifier 实现了一阶SGD学习程序。该算法迭代遍历训练样本，并根据给定的更新规则更新模型参数

\[w \leftarrow w - \eta \left[\alpha \frac{\partial R(w)}{\partial w} + \frac{\partial L(w^T x_i + b, y_i)}{\partial w}\right]\]

其中 \(\eta\) 是学习率，控制参数空间中的步长。截距 \(b\) 以类似方式更新，但不进行正则化（对于稀疏矩阵，还有额外的衰减，详见 实现细节 ）。

学习率 \(\eta\) 可以是恒定的或逐渐衰减的。对于分类，默认的学习率计划（ learning_rate='optimal' ）由以下公式给出

\[\eta^{(t)} = \frac {1}{\alpha (t_0 + t)}\]

其中 \(t\) 是时间步（总共有 n_samples * n_iter 个时间步），\(t_0\) 是根据Léon Bottou提出的启发式方法确定的。 使得预期的初始更新与权重的预期大小相当（这假设训练样本的范数大约为1）。确切的定义可以在 BaseSGD 中的 _init_t 找到。

对于回归，默认的学习率计划是逆缩放（ learning_rate='invscaling' ），由以下公式给出：

\[\eta^{(t)} = \frac{eta_0}{t^{power\_t}}\]

其中 \(eta_0\) 和 \(power\_t\) 是由用户通过 eta0 和 power_t 选择的超参数。

对于恒定的学习率，使用 learning_rate='constant' 并通过 eta0 指定学习率。

对于自适应递减的学习率，使用 learning_rate='adaptive' 并通过 eta0 指定起始学习率。当达到停止标准时，学习率除以5，并且算法不会停止。当学习率低于1e-6时，算法停止。

模型参数可以通过 coef_ 和 intercept_ 属性访问： coef_ 保存权重 \(w\) ，而 intercept_ 保存 \(b\) 。

当使用平均SGD（通过 average 参数）时， coef_ 被设置为所有更新的平均权重：

coef_ \(= \frac{1}{T} \sum_{t=0}^{T-1} w^{(t)}\) ，

其中 \(T\) 是总更新次数，可以在 t_ 属性中找到。

1.5.7. 实现细节#

SGD的实现受到[#1]_的 随机梯度SVM 的影响。 类似于SvmSGD， 权重向量被表示为一个标量和一个向量的乘积，这使得在L2正则化的情况下可以进行有效的权重更新。 对于稀疏输入 X ，截距以较小的学习率（乘以0.01）更新，以考虑到它更频繁地更新的情况。训练样本按顺序选取，并且在每个观察到的样本之后降低学习率。我们采用了[#2]_中的学习率计划。 对于多类分类，采用“一对多”方法。 我们使用 [9] 中提出的截断梯度算法进行 L1 正则化（以及弹性网络）。 代码是用 Cython 编写的。

On this page
Show Source