3.5. 验证曲线：绘制分数以评估模型#

每个估计器都有其优点和缺点。其泛化误差可以分解为偏差、方差和噪声。估计器的**偏差**是其对不同训练集的平均误差。估计器的**方差**表示其对不同训练集的敏感程度。噪声是数据的属性。

在下面的图中，我们看到了一个函数 \(f(x) = \cos (\frac{3}{2} \pi x)\) 和该函数的一些噪声样本。我们使用三种不同的估计器来拟合该函数：具有1次、4次和15次多项式特征的线性回归。我们看到，第一个估计器最多只能提供一个很差的拟合，因为模型过于简单（高偏差），第二个估计器几乎完美地拟合了它，而最后一个估计器完美地拟合了训练数据，但没有很好地拟合真实函数，即它对不同的训练数据非常敏感（高方差）。

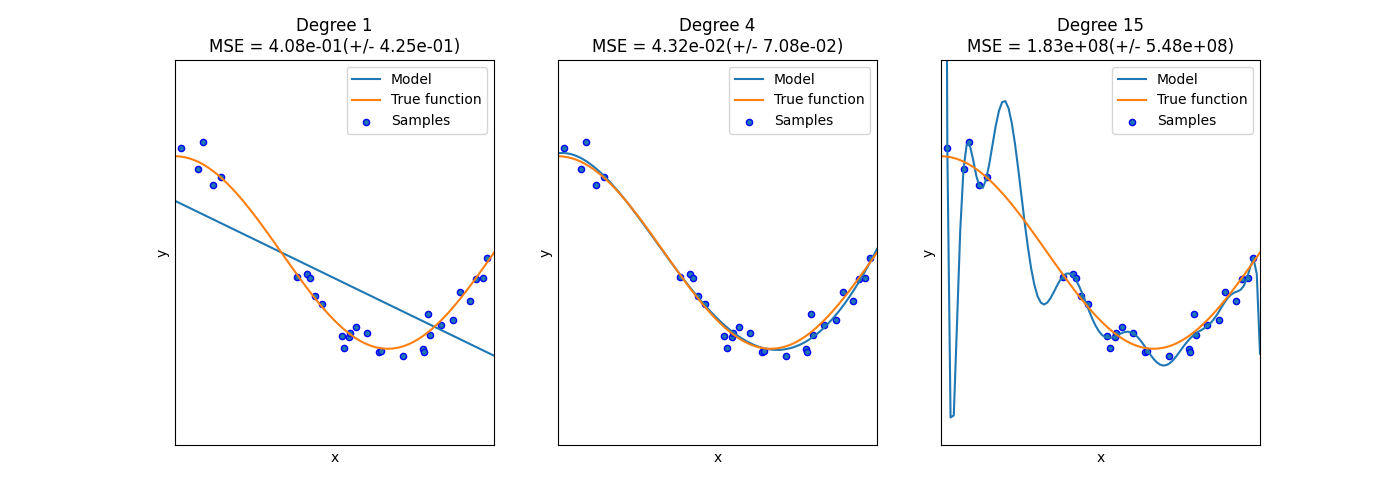
../_images/sphx_glr_plot_underfitting_overfitting_001.png

偏差和方差是估计器的固有属性，我们通常需要选择学习算法和超参数，以使偏差和方差都尽可能低（参见 偏差-方差困境 ）。另一种减少模型方差的方法是使用更多的训练数据。然而，只有在真实函数过于复杂以至于无法用具有较低方差的估计器来近似时，才应该收集更多的训练数据。

在我们在示例中看到的简单一维问题中， 很容易看出估计器是否存在偏差或方差问题。然而，在高维空间中，模型可能变得非常难以可视化。因此，使用下面描述的工具通常是有帮助的。

示例

3.5.1. 验证曲线#

为了验证模型，我们需要一个评分函数（参见 度量和评分：量化预测质量 ），例如分类器的准确性。选择估计器的多个超参数的正确方法是当然使用网格搜索或类似方法（参见 调整估计器的超参数 ），这些方法在验证集或多个验证集上选择具有最高分数的超参数。请注意，如果我们基于验证分数优化超参数，验证分数会有偏差，不再是一个好的泛化估计。为了得到正确的泛化估计，我们必须在另一个测试集上计算分数。

然而，有时绘制单个超参数对训练分数和验证分数的影响是有帮助的，以找出估计器在某些超参数值下是否过拟合或欠拟合。

函数 validation_curve 在这种情况下可以提供帮助:

>>> import numpy as np
>>> from sklearn.model_selection import validation_curve
>>> from sklearn.datasets import load_iris
>>> from sklearn.svm import SVC

>>> np.random.seed(0)
>>> X, y = load_iris(return_X_y=True)
>>> indices = np.arange(y.shape[0])
>>> np.random.shuffle(indices)
>>> X, y = X[indices], y[indices]

>>> train_scores, valid_scores = validation_curve(
...     SVC(kernel="linear"), X, y, param_name="C", param_range=np.logspace(-7, 3, 3),
... )
>>> train_scores
array([[0.90..., 0.94..., 0.91..., 0.89..., 0.92...],

       [0.9... , 0.92..., 0.93..., 0.92..., 0.93...],
       [0.97..., 1...   , 0.98..., 0.97..., 0.99...]])
>>> valid_scores
array([[0.9..., 0.9... , 0.9... , 0.96..., 0.9... ],
       [0.9..., 0.83..., 0.96..., 0.96..., 0.93...],
       [1.... , 0.93..., 1....  , 1....  , 0.9... ]])

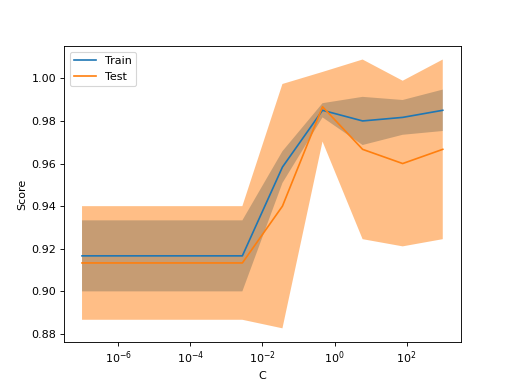
如果你想仅绘制验证曲线，使用类 ValidationCurveDisplay 比手动在调用 validation_curve 的结果上使用 matplotlib 更为直接。你可以类似地使用方法 from_estimator 来生成并绘制验证曲线：

from sklearn.datasets import load_iris
from sklearn.model_selection import ValidationCurveDisplay
from sklearn.svm import SVC
from sklearn.utils import shuffle
X, y = load_iris(return_X_y=True)
X, y = shuffle(X, y, random_state=0)
ValidationCurveDisplay.from_estimator(
   SVC(kernel="linear"), X, y, param_name="C", param_range=np.logspace(-7, 3, 10)
)
../_images/learning_curve-1.png

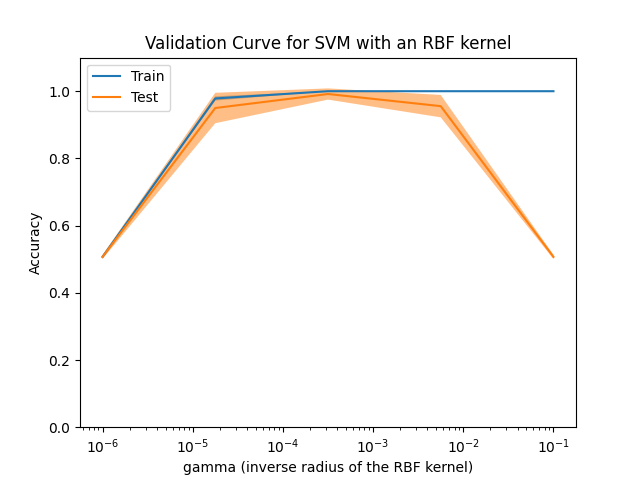
如果训练分数和验证分数都很低，则估计器会欠拟合。如果训练分数高而验证分数低，则估计器过拟合，否则它工作得很好。通常情况下，低训练分数和高验证分数是不可能的。欠拟合、过拟合和正常工作的模型在下图中展示，我们在 digits 数据集上改变带有 RBF 核的 SVM 的参数 gamma 。

../_images/sphx_glr_plot_validation_curve_001.png

3.5.2. 学习曲线#

学习曲线展示了估计器的验证和训练分数

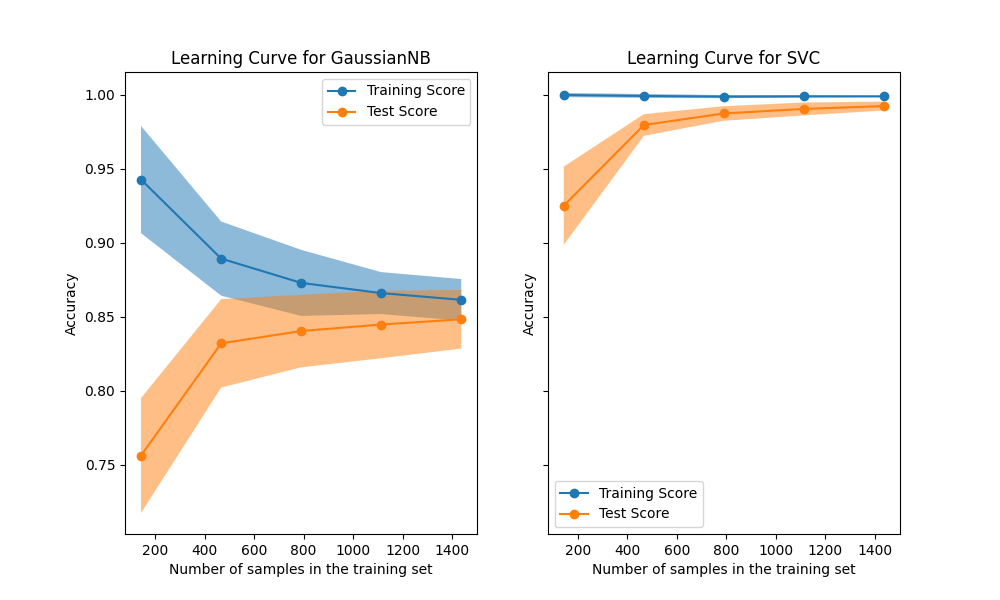
对于不同数量的训练样本。它是一个工具，用于找出我们从增加更多训练数据中获益多少，以及估计器是否更受方差误差或偏差误差的影响。考虑以下示例，我们绘制了一个朴素贝叶斯分类器和一个SVM的学习曲线。

对于朴素贝叶斯，随着训练集大小的增加，验证分数和训练分数都收敛到一个相当低的值。因此，我们可能不会从更多的训练数据中获益太多。

相比之下，对于少量数据，SVM的训练分数远高于验证分数。增加更多的训练样本很可能会提高泛化能力。

../_images/sphx_glr_plot_learning_curve_001.png

我们可以使用函数 learning_curve 来生成绘制这种学习曲线所需的值（已使用的样本数量、训练集上的平均分数和验证集上的平均分数）:

>>> from sklearn.model_selection import learning_curve
>>> from sklearn.svm import SVC

>>> train_sizes, train_scores, valid_scores = learning_curve(
...     SVC(kernel='linear'), X, y, train_sizes=[50, 80, 110], cv=5)
>>> train_sizes
array([ 50, 80, 110])
>>> train_scores
array([[0.98..., 0.98 , 0.98..., 0.98..., 0.98...],
       [0.98..., 1.   , 0.98..., 0.98..., 0.98...],
       [0.98..., 1.   , 0.98..., 0.98..., 0.99...]])
>>> valid_scores
array([[1. ,  0.93...,  1. ,  1. ,  0.96...],
       [1. ,  0.96...,  1. ,  1. ,  0.96...],
       [1. ,  0.96...,  1. ,  1. ,  0.96...]])

如果你打算仅绘制学习曲线，类 LearningCurveDisplay 将更易于使用。你可以使用方法 from_estimator 类似地 to learning_curve 以生成并绘制学习曲线：

从 sklearn.datasets 导入 load_iris
从 sklearn.model_selection 导入 LearningCurveDisplay
从 sklearn.svm 导入 SVC
从 sklearn.utils 导入 shuffle
X, y = load_iris(return_X_y=True)
X, y = shuffle(X, y, random_state=0)
LearningCurveDisplay.from_estimator(
   SVC(kernel="linear"), X, y, train_sizes=[50, 80, 110], cv=5)
On this page
Show Source