6.7. 核近似

这个子模块包含了一些函数，这些函数近似于某些核所对应的特征映射，例如在支持向量机中使用的核（参见 支持向量机 ）。 以下特征函数执行输入的非线性变换，可以作为线性分类或其他算法的基。

使用近似的显式特征映射相比于使用 核技巧 （该技巧隐式地利用特征映射）的优势在于，显式映射更适合在线学习，并且可以显著降低处理大型数据集时的学习成本。 标准的核化支持向量机在处理大型数据集时扩展性不佳，但使用近似核映射，可以更有效地使用线性支持向量机。 特别是，将核映射近似与 SGDClassifier 结合使用，可以使大型数据集上的非线性学习成为可能。

由于使用近似嵌入的实证工作不多，建议在可能的情况下将结果与精确的核方法进行比较。

See also

多项式回归：通过基函数扩展线性模型 用于精确的多项式变换。

6.7.1. Nystroem 方法用于核近似

Nystroem 方法，如在 Nystroem 中实现的，是一种通用的方法，用于核的降秩近似。它通过无放回地抽样数据集的行/列来实现这一点，这些数据集是核评估的对象。虽然精确方法的计算复杂度为 \(\mathcal{O}(n^3_{\text{samples}})\) ，但近似的复杂度为 \(\mathcal{O}(n^2_{\text{components}} \cdot n_{\text{samples}})\) ，其中可以设置 \(n_{\text{components}} \ll n_{\text{samples}}\) 而不会影响性能。 性能显著下降 [WS2001]。

我们可以根据数据的特征构建核矩阵 \(K\) 的特征分解，然后将其分为采样和未采样数据点。

\[\begin{split}K = U \Lambda U^T = \begin{bmatrix} U_1 \\ U_2\end{bmatrix} \Lambda \begin{bmatrix} U_1 \\ U_2 \end{bmatrix}^T = \begin{bmatrix} U_1 \Lambda U_1^T & U_1 \Lambda U_2^T \\ U_2 \Lambda U_1^T & U_2 \Lambda U_2^T \end{bmatrix} \equiv \begin{bmatrix} K_{11} & K_{12} \\ K_{21} & K_{22} \end{bmatrix}\end{split}\]

其中：

• \(U\) 是正交矩阵

• \(\Lambda\) 是特征值的对角矩阵

• \(U_1\) 是所选样本的正交矩阵

• \(U_2\) 是未选样本的正交矩阵

已知 \(U_1 \Lambda U_1^T\) 可以通过正交化矩阵 \(K_{11}\) 获得，并且 \(U_2 \Lambda U_1^T\) 及其转置可以被评估，唯一剩下的待阐明项是 \(U_2 \Lambda U_2^T\) 。为此，我们可以用已经评估过的矩阵来表示它：

\[\begin{split}\begin{align} U_2 \Lambda U_2^T &= \left(K_{21} U_1 \Lambda^{-1}\right) \Lambda \left(K_{21} U_1 \Lambda^{-1}\right)^T \\&= K_{21} U_1 (\Lambda^{-1} \Lambda) \Lambda^{-1} U_1^T K_{21}^T \\&= K_{21} U_1 \Lambda^{-1} U_1^T K_{21}^T \\&= K_{21} K_{11}^{-1} K_{21}^T \\&= \left( K_{21} K_{11}^{-\frac12} \right) \left( K_{21} K_{11}^{-\frac12} \right)^T .\end{align}\end{split}\]

在 fit 过程中，类 Nystroem 评估基 \(U_1\) ，并计算归一化常数 \(K_{11}^{-\frac12}\) 。之后，在 transform 过程中，核矩阵在基（由 components_ 属性给出）和新数据点 X 之间确定。然后，该矩阵乘以 normalization_ 矩阵以得到最终结果。

默认情况下，Nystroem 使用 rbf 核，但它可以使用任何核。 函数或预计算的核矩阵。使用的样本数量——这也是计算特征的维度——由参数 n_components 给出。

示例

• 请参阅名为 时间相关特征工程 的示例， 该示例展示了一个使用 Nystroem 核的高效机器学习流水线。

6.7.2. 径向基函数核

RBFSampler 构造了径向基函数核（也称为 随机厨房水槽 [RR2007]）的近似映射。 这种变换可以用于在应用线性算法之前显式地建模核映射，例如线性 SVM:

>>> from sklearn.kernel_approximation import RBFSampler
>>> from sklearn.linear_model import SGDClassifier
>>> X = [[0, 0], [1, 1], [1, 0], [0, 1]]
>>> y = [0, 0, 1, 1]
>>> rbf_feature = RBFSampler(gamma=1, random_state=1)
>>> X_features = rbf_feature.fit_transform(X)
>>> clf = SGDClassifier(max_iter=5)
>>> clf.fit(X_features, y)
SGDClassifier(max_iter=5)
>>> clf.score(X_features, y)
1.0

该映射依赖于核值的蒙特卡洛近似。 fit 函数执行蒙特卡洛采样，而 transform 方法执行数据的映射。 由于过程的固有随机性，不同调用 fit 函数的结果可能会有所不同。

fit 函数接受两个参数： n_components ，即特征变换的目标维度，以及 gamma ，RBF 核的参数。

较高的 n_components 将产生更好的核近似，并产生更类似于核 SVM 的结果。请注意，“拟合”特征函数实际上并不依赖于传递给 fit 函数的数据。 仅使用数据的维度。 方法的详细信息可以在 [RR2007] 中找到。

对于给定的 n_components 值，RBFSampler 通常不如 Nystroem 准确。然而，RBFSampler 的计算成本较低，使得使用更大的特征空间更加高效。

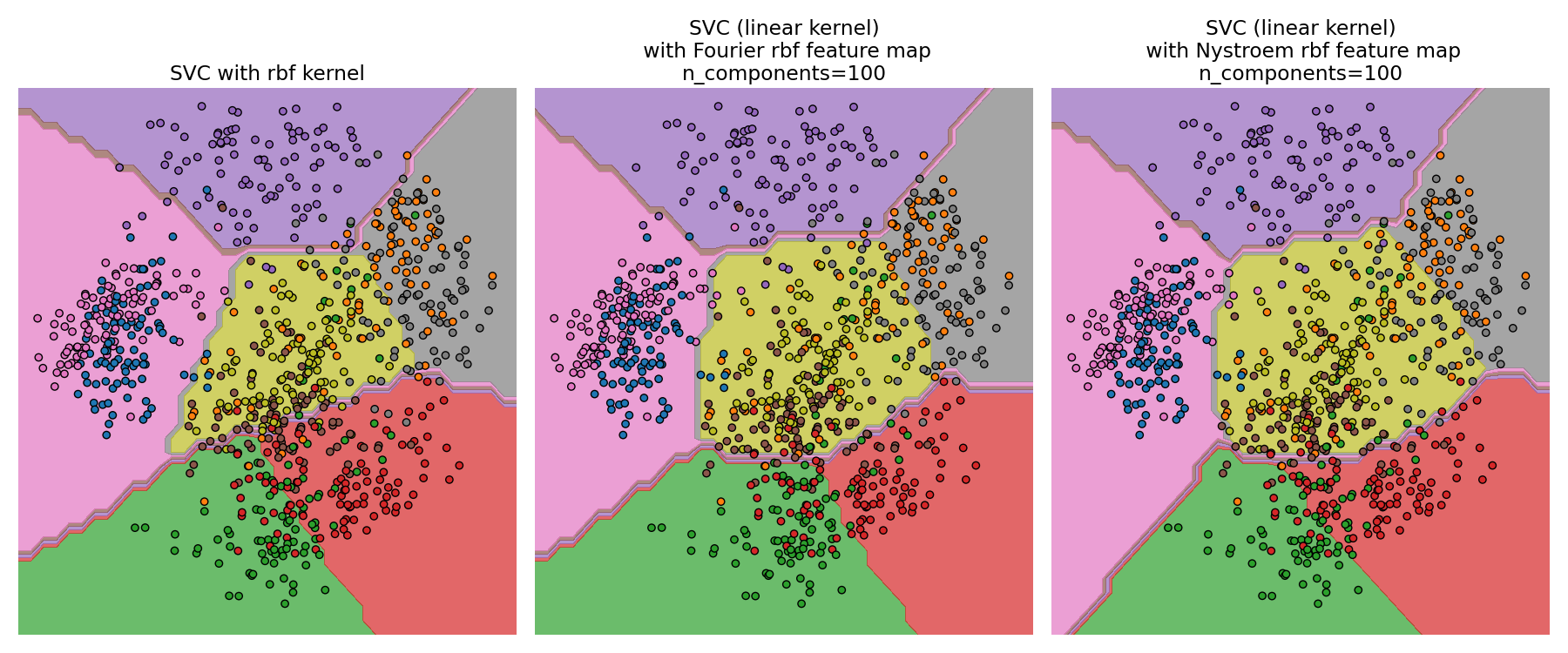
比较精确的 RBF 核（左侧）与近似核（右侧）

示例

• RBF核的显式特征映射近似

6.7.3. 加性 Chi Squared 核

加性 Chi Squared 核是一种用于直方图的核函数，常用于计算机视觉领域。

此处使用的加性 Chi Squared 核定义为

\[k(x, y) = \sum_i \frac{2x_iy_i}{x_i+y_i}\]

这与 sklearn.metrics.pairwise.additive_chi2_kernel 不完全相同。[VZ2010] 的作者倾向于上述版本，因为它总是正定的。 由于该核是加性的，可以分别处理所有分量 \(x_i\) 进行嵌入。这使得可以在常规间隔内采样傅里叶变换，而不是使用蒙特卡洛采样进行近似。

类 AdditiveChi2Sampler 实现了这种分量级的确定性采样。每个分量被采样 \(n\) 次，每个输入维度产生 \(2n+1\) 维（两倍的倍数来自傅里叶变换的实部和虚部）。 在文献中，通常选择 \(n\) 为 1 或 2，将数据集转换为大小 n_samples * 5 * n_features （在 \(n=2\) 的情况下）。

AdditiveChi2Sampler 提供的近似特征映射可以与 RBFSampler 提供的近似特征映射结合，以产生一个近似的特征映射。 指数卡方核的特征图。 详情请参阅 [VZ2010]，与 RBFSampler 结合的说明请参阅 [VVZ2010]。

6.7.4. 偏斜卡方核

偏斜卡方核定义如下：

\[k(x,y) = \prod_i \frac{2\sqrt{x_i+c}\sqrt{y_i+c}}{x_i + y_i + 2c}\]

它具有类似于计算机视觉中常用的指数卡方核的性质，但允许对特征图进行简单的蒙特卡洛近似。

SkewedChi2Sampler 的使用方法与上述 RBFSampler 的描述相同。唯一的区别在于自由参数，称为 \(c\) 。 关于此映射的动机和数学细节，请参阅 [LS2010]。

6.7.5. 通过张量草图进行多项式核近似

多项式核 是一种流行的核函数，定义如下：

\[k(x, y) = (\gamma x^\top y +c_0)^d\]

其中：

• x , y 是输入向量

• d 是核的度数

直观上，多项式核的特征空间包含所有可能的度数为 d 的输入特征之间的乘积，这使得使用此核的学习算法能够考虑特征之间的交互作用。

张量草图 [PP2013] 方法，如在 PolynomialCountSketch 中实现的，是一种可扩展的、与输入数据无关的多项式核近似方法。它基于计数草图 [WIKICS] [CCF2002] 的概念，这是一种类似于特征哈希的降维技术，但使用多个独立的哈希函数。张量草图获取两个向量（或向量与自身的）外积的计数草图，这可以作为多项式核特征空间的近似。特别是，它避免了显式计算 外积, TensorSketch 计算向量的 Count Sketch, 然后通过快速傅里叶变换进行多项式乘法来计算它们的外积的 Count Sketch。

方便的是, TensorSketch 的训练阶段仅包括初始化一些随机变量。因此, 它与输入数据无关, 即它仅依赖于输入特征的数量, 而不依赖于数据值。此外, 这种方法可以在 \(\mathcal{O}(n_{\text{samples}}(n_{\text{features}} + n_{\text{components}} \log(n_{\text{components}})))\) 时间内转换样本, 其中 \(n_{\text{components}}\) 是期望的输出维度, 由 n_components 决定。

示例

• 通过多项式核近似实现可扩展学习

6.7.6. 数学细节

支持向量机或核化 PCA 等核方法依赖于再生核希尔伯特空间的性质。对于任何正定核函数 \(k\) (称为 Mercer 核), 可以保证存在一个映射 \(\phi\) 到希尔伯特空间 \(\mathcal{H}\) , 使得

\[k(x,y) = \langle \phi(x), \phi(y) \rangle\]

其中 \(\langle \cdot, \cdot \rangle\) 表示希尔伯特空间中的内积。

如果算法 (如线性支持向量机或 PCA) 仅依赖于数据点 \(x_i\) 的标量积, 可以使用 \(k(x_i, x_j)\) 的值, 这相当于将算法应用于映射后的数据点 \(\phi(x_i)\) 。使用 \(k\) 的优点是映射 \(\phi\) 永远不需要显式计算, 允许任意大的特征 (甚至是无限的)。

核方法的一个缺点是, 在优化过程中可能需要存储许多核值 \(k(x_i, x_j)\) 。如果将核化分类器应用于新数据 \(y_j\) , \(k(x_i, y_j)\) 需要被计算以进行预测，可能针对训练集中的许多不同的 \(x_i\) 。

此子模块中的类允许近似嵌入 \(\phi\) ，从而显式地处理表示 \(\phi(x_i)\) ，这避免了应用核函数或存储训练样本的需要。

参考文献

[WS2001]

“Using the Nyström method to speed up kernel machines” Williams, C.K.I.; Seeger, M. - 2001.

[RR2007] (1,2)

“Random features for large-scale kernel machines” Rahimi, A. and Recht, B. - Advances in neural information processing 2007,

[LS2010]

“Random Fourier approximations for skewed multiplicative histogram kernels” Li, F., Ionescu, C., and Sminchisescu, C. - Pattern Recognition, DAGM 2010, Lecture Notes in Computer Science.

[VZ2010] (1,2)

“Efficient additive kernels via explicit feature maps” Vedaldi, A. and Zisserman, A. - Computer Vision and Pattern Recognition 2010

[VVZ2010]

“Generalized RBF feature maps for Efficient Detection” Vempati, S. and Vedaldi, A. and Zisserman, A. and Jawahar, CV - 2010

[PP2013]

“Fast and scalable polynomial kernels via explicit feature maps” Pham, N., & Pagh, R. - 2013

[CCF2002]

“Finding frequent items in data streams” Charikar, M., Chen, K., & Farach-Colton - 2002

[WIKICS]

`”Wikipedia: Count sketch”

<https://en.wikipedia.org/wiki/Count_sketch>`_