2.8. 密度估计

密度估计介于无监督学习、特征工程和数据建模之间。一些最流行和有用的密度估计技术包括混合模型，如高斯混合模型（GaussianMixture ），以及基于邻近的方法，如核密度估计（KernelDensity ）。高斯混合模型在 聚类 的背景下进行了更全面的讨论，因为该技术也作为一种无监督聚类方案有用。

密度估计是一个非常简单的概念，大多数人已经熟悉一种常见的密度估计技术：直方图。

2.8.1. 密度估计：直方图

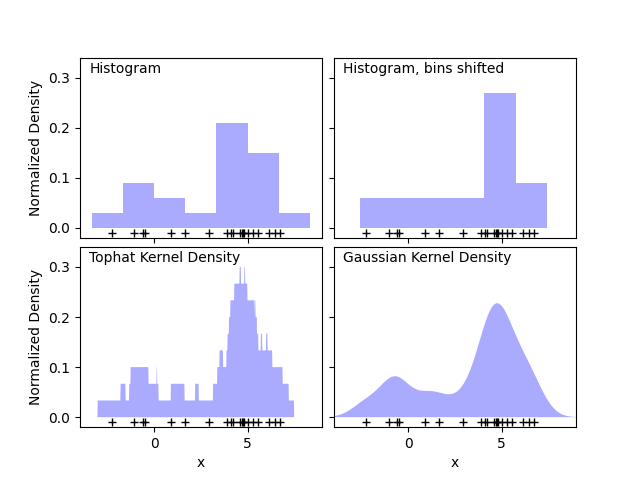
直方图是一种简单的数据可视化方法，其中定义了若干区间，并统计每个区间内的数据点数量。下图左上角的面板展示了一个直方图的例子：

然而，直方图的一个主要问题是区间选择的差异可能会对最终的可视化结果产生不成比例的影响。考虑上图右上角的面板。它显示了与相同数据重叠的直方图，但区间向右移动。这两个可视化结果看起来完全不同，可能会导致对数据的不同解释。

直观上，可以将直方图视为点的块堆叠，每个点一个块。通过在适当的网格空间中堆叠块，我们可以恢复直方图。但是，如果我们不将块堆叠在规则的网格上， 我们将每个块以其代表的点为中心，并在每个位置累加总高度？这个想法导致了左下角的可视化。它可能不像直方图那样整洁，但数据驱动块位置的事实意味着它更好地代表了基础数据。

这种可视化是*核密度估计*的一个例子，在这种情况下使用了一个平顶核（即每个点上的方形块）。通过使用更平滑的核，我们可以恢复更平滑的分布。右下角的图显示了一个高斯核密度估计，其中每个点对总体贡献一个高斯曲线。结果是一个平滑的密度估计，它源自数据，并作为一个强大的非参数模型来表示点的分布。

2.8.2. 核密度估计

scikit-learn中的核密度估计在:class:~sklearn.neighbors.KernelDensity 估计器中实现，该估计器使用Ball Tree或KD Tree进行高效查询（参见:ref:neighbors 以讨论这些）。尽管上面的例子为了简单起见使用了一维数据集，但核密度估计可以在任意数量的维度中执行，尽管在实践中维度灾难会导致在高维度中性能下降。

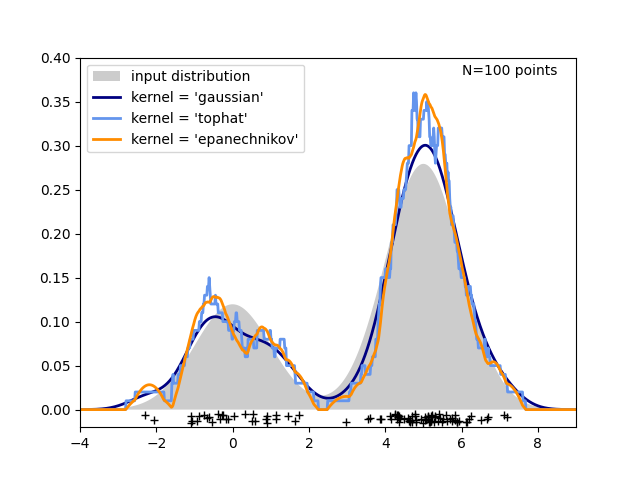
在下面的图中，从双峰分布中抽取了100个点，并显示了三种核选择的核密度估计：

很明显，核形状如何影响结果分布的平滑度。scikit-learn的核密度估计器可以按如下方式使用：

>>> from sklearn.neighbors import KernelDensity
>>> import numpy as np
>>> X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])

>>> kde = KernelDensity(kernel='gaussian', bandwidth=0.2).fit(X)
>>> kde.score_samples(X)
array([-0.41075698, -0.41075698, -0.41076071, -0.41075698, -0.41075698,
       -0.41076071])

这里我们使用了 kernel='gaussian' ，如上所示。 在数学上，核是一个正函数 \(K(x;h)\) ，它受带宽参数 \(h\) 控制。 给定这个核形式，点 \(y\) 在一组点 \(x_i; i=1\cdots N\) 内的密度估计由以下公式给出：

\[\rho_K(y) = \sum_{i=1}^{N} K(y - x_i; h)\]

这里的带宽充当一个平滑参数，控制结果中偏差和方差之间的权衡。 较大的带宽会导致非常平滑（即高偏差）的密度分布。较小的带宽会导致不平滑（即高方差）的密度分布。

参数 bandwidth 控制这种平滑。可以手动设置此参数，也可以使用 Scott 和 Silvermann 的估计方法。

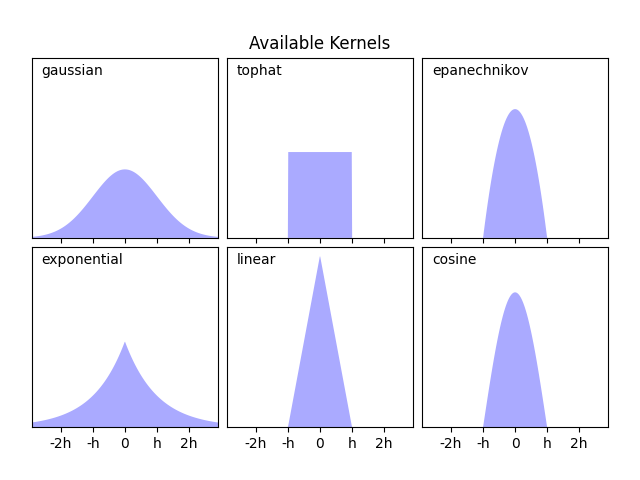
KernelDensity 实现了几种常见的核形式，如下所示：

核的数学表达式

这些核的形式如下：

• 高斯核 ( kernel = 'gaussian' )

  \(K(x; h) \propto \exp(- \frac{x^2}{2h^2} )\)

• Tophat 核 ( kernel = 'tophat' )

  \(K(x; h) \propto 1\) 如果 \(x < h\)

• Epanechnikov 核 ( kernel = 'epanechnikov' )

  \(K(x; h) \propto 1 - \frac{x^2}{h^2}\)

• 指数核 ( kernel = 'exponential' )

  \(K(x; h) \propto \exp(-x/h)\)

• 线性核 ( kernel = 'linear' )

  \(K(x; h) \propto 1 - x/h\) 如果 \(x < h\)

• 余弦核 ( kernel = 'cosine' )

  \(K(x; h) \propto \cos(\frac{\pi x}{2h})\) 如果 \(x < h\)

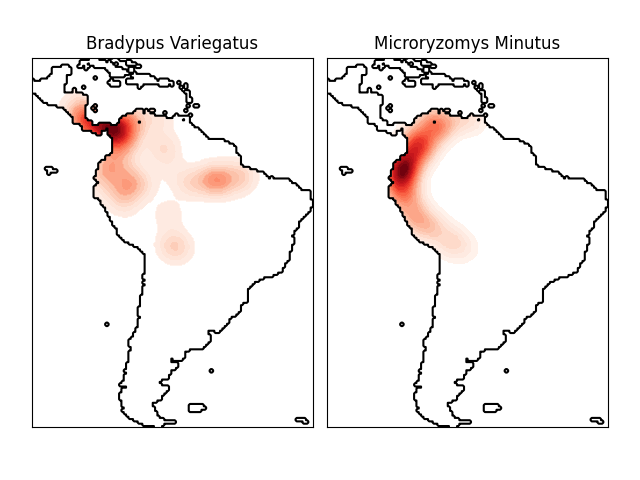
核密度估计器可以使用任何有效的距离度量（参见 DistanceMetric 以获取可用度量列表），尽管结果仅在欧几里得度量下正确归一化。一个特别有用的度量是 Haversine 距离 ，它测量球面上点之间的角距离。以下是一个使用核密度估计进行地理空间数据可视化的示例，在这种情况下，是南美洲大陆上两种不同物种观测分布的情况：

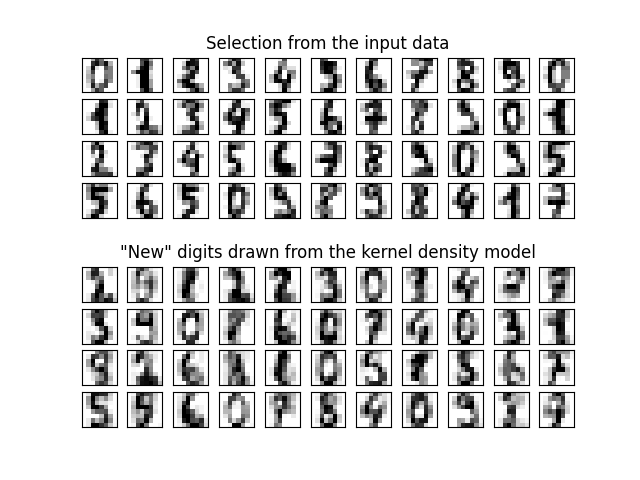
核密度估计的另一个有用应用是学习数据集的非参数生成模型，以便从该生成模型中高效地抽取新样本。以下是一个使用此过程创建一组新的手写数字的示例，使用在数据的主成分分析（PCA）投影上学到的 Gaussian 核：

“新”数据由输入数据的线性组合组成，权重根据 KDE 模型概率性地抽取。

示例

• 简单的一维核密度估计 : 一维简单核密度估计的计算。

• 核密度估计 : 使用核密度估计学习手写数字数据的生成模型，并从此模型中抽取新样本的示例。

• 物种分布的核密度估计 : 使用核密度估计的示例，展示南美洲大陆上两种不同物种观测分布的情况。

使用 Haversine 距离度量来可视化地理空间数据