1.8. 交叉分解#
交叉分解模块包含属于“偏最小二乘”家族的**监督**降维和回归估计器。
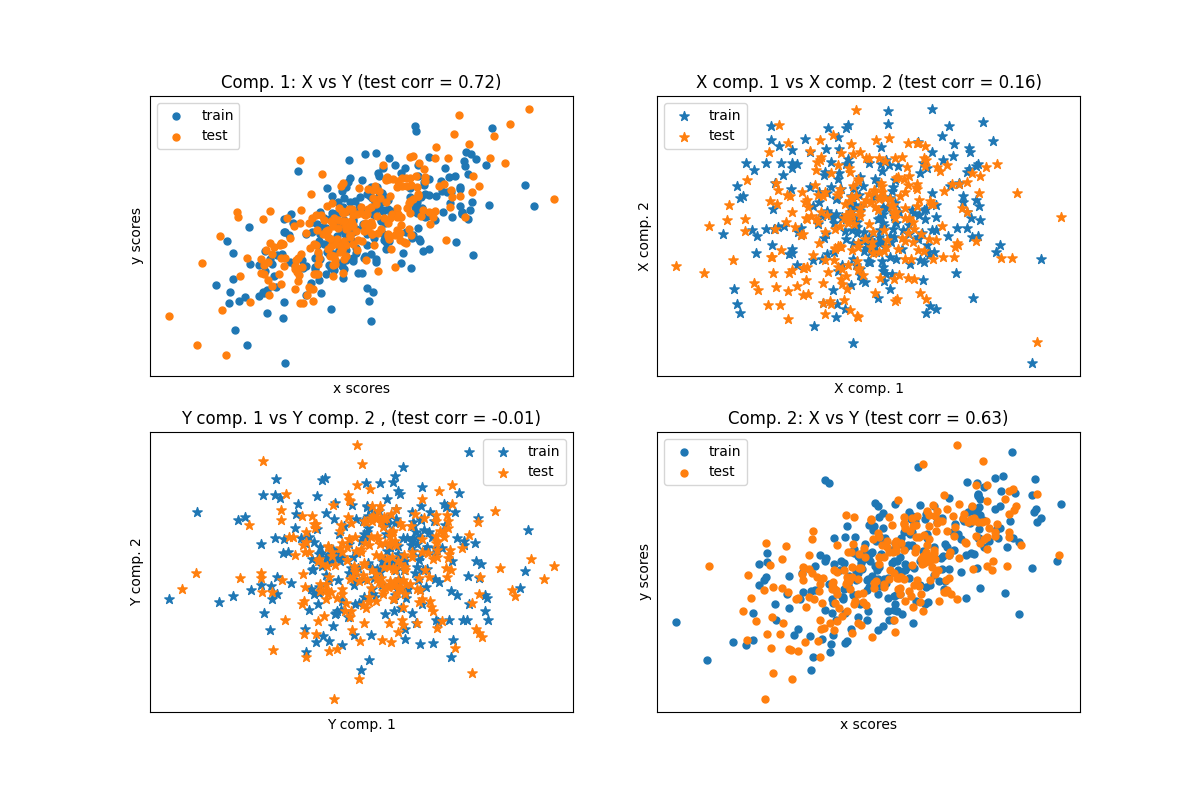
交叉分解算法在两个矩阵（X和Y）之间找到基本关系。它们是用于建模这两个空间中协方差结构的潜在变量方法。它们将尝试在X空间中找到解释Y空间中最大多维方差方向的多维方向。换句话说，PLS将 X 和 Y 投影到一个较低维度的子空间中，使得 transformed(X) 和 transformed(Y) 之间的协方差最大化。
PLS与 主成分回归 （PCR）有相似之处，其中样本首先被投影到一个较低维度的子空间中，然后使用 transformed(X) 预测目标 y 。PCR的一个问题是降维是无监督的，可能会丢失一些重要的变量：PCR会保留方差最大的特征，但有可能方差较小的特征对预测目标是有用的。在某种程度上，PLS允许进行类似的降维，但考虑了目标 y 。以下示例说明了这一事实：
* 主成分回归与偏最小二乘回归 。
除了CCA之外，PLS估计器特别适用于预测变量矩阵的变量多于观测值的情况，以及存在多重共线性时。 特征间的多重共线性。相比之下，标准线性回归在这些情况下会失败，除非它被正则化。
本模块中包含的类有 PLSRegression 、PLSCanonical 、CCA 和 PLSSVD
1.8.1. PLSCanonical#
我们在这里描述 PLSCanonical 中使用的算法。其他估计器使用该算法的变体，并在下面详细说明。我们建议参考 [1] 部分以获取更多详细信息和这些算法之间的比较。在 [1] 中，PLSCanonical 对应于 “PLSW2A”。
给定两个中心化的矩阵 \(X \in \mathbb{R}^{n \times d}\) 和 \(Y \in \mathbb{R}^{n \times t}\) ，以及组件数量 \(K\) ，PLSCanonical 的步骤如下：
将 \(X_1\) 设为 \(X\) ，将 \(Y_1\) 设为 \(Y\) 。然后，对于每个 \(k \in [1, K]\) ：
计算 \(u_k \in \mathbb{R}^d\) 和 \(v_k \in \mathbb{R}^t\) ，即交叉协方差矩阵 \(C = X_k^T Y_k\) 的第一左奇异向量和右奇异向量。\(u_k\) 和 \(v_k\) 被称为 权重。根据定义，\(u_k\) 和 \(v_k\) 被选择以最大化投影 \(X_k\) 和投影目标之间的协方差，即 \(\text{Cov}(X_k u_k, Y_k v_k)\) 。
在奇异向量上投影 \(X_k\) 和 \(Y_k\) 以获得 得分：\(\xi_k = X_k u_k\) 和 \(\omega_k = Y_k v_k\)
在 \(\xi_k\) 上回归 \(X_k\) ，即找到一个向量 \(\gamma_k \in \mathbb{R}^d\) ，使得秩为 1 的矩阵 \(\xi_k \gamma_k^T\) 尽可能接近 \(X_k\) 。对 \(Y_k\) 和 \(\omega_k\) 进行相同的操作以获得 \(\delta_k\) 。向量 \(\gamma_k\) 和 \(\delta_k\) 被称为 载荷。
收缩 \(X_k\) 和 \(Y_k\) ，即减去秩为 1 的近似值：\(X_{k+1} = X_k - \xi_k \gamma_k^T\) ，以及 \(Y_{k + 1} = Y_k - \omega_k \delta_k^T\) 。
最终，我们将 \(X\) 近似为秩-1矩阵的和： \(X = \Xi \Gamma^T\) ，其中 \(\Xi \in \mathbb{R}^{n \times K}\) 包含其列中的分数，而 \(\Gamma^T \in \mathbb{R}^{K \times d}\) 包含其行中的载荷。类似地，对于 \(Y\) ，我们有 \(Y = \Omega \Delta^T\) 。
请注意，分数矩阵 \(\Xi\) 和 \(\Omega\) 分别对应于训练数据 \(X\) 和 \(Y\) 的投影。
步骤 a) 可以通过两种方式执行：要么通过计算 \(C\) 的完整 SVD 并仅保留具有最大奇异值的奇异向量，要么通过直接使用幂方法（参见 [1] 中的第 11.3 节）计算奇异向量，这对应于 algorithm 参数的 'nipals' 选项。
#转换数据
要将 \(X\) 转换为 \(\bar{X}\) ，我们需要找到一个投影矩阵 \(P\) ，使得 \(\bar{X} = XP\) 。我们知道对于训练数据，\(\Xi = XP\) ，并且 \(X = \Xi \Gamma^T\) 。设 \(P = U(\Gamma^T U)^{-1}\) ，其中 \(U\) 是包含列中 \(u_k\) 的矩阵，我们有 \(XP = X U(\Gamma^T U)^{-1} = \Xi (\Gamma^T U) (\Gamma^T U)^{-1} = \Xi\) ，正如所愿。旋转矩阵 \(P\) 可以通过 x_rotations_ 属性访问。
类似地，\(Y\) 可以使用旋转矩阵 \(V(\Delta^T V)^{-1}\) 进行转换，通过 y_rotations_ 属性访问。
#预测目标 Y
为了预测某些数据 \(X\) 的目标，我们正在寻找一个系数矩阵 \(\beta \in R^{d \times t}\) ，使得 \(Y = X\beta\) 。
这个想法是尝试将转换后的目标 \(\Omega\) 作为转换后的样本 \(\Xi\) 的函数进行预测，通过计算 \(\alpha \in \mathbb{R}\) ，使得 \(\Omega = \alpha \Xi\) 。
然后，我们有 \(Y = \Omega \Delta^T = \alpha \Xi \Delta^T\) ，并且由于
\(\Xi\) 是我们拥有的转换后的训练数据，满足 \(Y = X \alpha P \Delta^T\) ，因此系数矩阵 \(\beta = \alpha P \Delta^T\) 。
\(\beta\) 可以通过 coef_ 属性访问。
1.8.2. PLSSVD#
PLSSVD 是之前描述的 PLSCanonical 的简化版本：它不是迭代地消减矩阵 \(X_k\) 和 \(Y_k\) ，而是只计算一次 \(C = X^TY\) 的 SVD，并将与最大奇异值对应的 n_components 个奇异向量存储在矩阵 U 和 V 中，对应于 x_weights_ 和 y_weights_ 属性。在这里，转换后的数据简单地为 transformed(X) = XU 和 transformed(Y) = YV 。
如果 n_components == 1 ，PLSSVD 和 PLSCanonical 是完全等价的。
1.8.3. PLSRegression#
PLSRegression 估计器与 PLSCanonical 在 algorithm='nipals' 时类似，有两个显著差异：
在计算 \(u_k\) 和 \(v_k\) 的幂方法的步骤 a) 中，\(v_k\) 从不归一化。
在步骤 c) 中，目标 \(Y_k\) 使用 \(X_k\) （即 \(\xi_k\) ）的投影来近似，而不是 \(Y_k\) （即 \(\omega_k\) ）的投影。换句话说，载荷计算是不同的。因此，步骤 d) 中的消减也会受到影响。
这两个修改影响了 predict 和 transform 的输出，与 PLSCanonical 不同。此外，虽然 PLSCanonical 中的组件数量受限于 min(n_samples, n_features, n_targets) ，但在这里的限制是 \(X^TX\) 的秩，即 min(n_samples, n_features) 。
PLSRegression 也被称为 PLS1（单个目标）和 PLS2（多个目标）。与 Lasso 类似，PLSRegression 是一种正则化线性回归的形式。
组件数量控制正则化的强度。
1.8.4. 典型相关分析#
典型相关分析（Canonical Correlation Analysis，CCA）是在PLS之前独立开发的。但事实证明，CCA 是PLS的一个特例，并且在文献中对应于PLS的“模式B”。
CCA 与:class:PLSCanonical 在步骤a）的幂方法中计算权重:math:u_k 和:math:v_k 的方式不同。详细信息可以在[1]的第10节中找到。
由于:class:CCA 涉及:math:X_k^TX_k 和:math:Y_k^TY_k 的逆运算，如果特征数量或目标数量大于样本数量，这个估计器可能会不稳定。
参考文献
示例