Note

Go to the end to download the full example code. or to run this example in your browser via Binder

通过多项式核近似实现可扩展学习#

本示例展示了如何使用 PolynomialCountSketch 高效生成多项式核特征空间近似。这用于训练线性分类器，以近似核化分类器的准确性。

我们使用 Covtype 数据集 [2]，尝试重现 Tensor Sketch 原始论文中的实验 [1]，即由 PolynomialCountSketch 实现的算法。

首先，我们计算线性分类器在原始特征上的准确性。然后，我们在由 PolynomialCountSketch 生成的不同数量的特征（ n_components ）上训练线性分类器，以可扩展的方式近似核化分类器的准确性。

# 作者：scikit-learn 开发者
# SPDX-License-Identifier: BSD-3-Clause

准备数据#

加载Covtype数据集，该数据集包含581,012个样本，每个样本有54个特征，分布在6个类别中。该数据集的目标是仅通过制图变量（不包括遥感数据）预测森林覆盖类型。加载后，我们将其转换为二分类问题，以匹配LIBSVM网页上的数据集版本[2]，该版本在[1]中使用。

from sklearn.datasets import fetch_covtype

X, y = fetch_covtype(return_X_y=True)

y[y != 2] = 0
y[y == 2] = 1  # We will try to separate class 2 from the other 6 classes.

划分数据#

我们在这里选择5000个样本用于训练，10000个样本用于测试。要真正重现原始Tensor Sketch论文中的结果，请选择100000个样本用于训练。

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(
    X, y, train_size=5_000, test_size=10_000, random_state=42
)

特征归一化#

现在将特征缩放到 [0, 1] 范围，以匹配 LIBSVM 网页中的数据集格式，然后像原始 Tensor Sketch 论文 [1] 中那样归一化到单位长度。

from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import MinMaxScaler, Normalizer

mm = make_pipeline(MinMaxScaler(), Normalizer())
X_train = mm.fit_transform(X_train)
X_test = mm.transform(X_test)

建立基线模型#

作为基线，在原始特征上训练一个线性SVM并打印准确率。我们还测量并存储准确率和训练时间，以便稍后绘制它们。

import time

from sklearn.svm import LinearSVC

results = {}

lsvm = LinearSVC()
start = time.time()
lsvm.fit(X_train, y_train)
lsvm_time = time.time() - start
lsvm_score = 100 * lsvm.score(X_test, y_test)

results["LSVM"] = {"time": lsvm_time, "score": lsvm_score}
print(f"Linear SVM score on raw features: {lsvm_score:.2f}%")

Linear SVM score on raw features: 75.62%

建立核近似模型#

然后，我们在由 PolynomialCountSketch 生成的特征上训练线性 SVM，使用不同的 n_components 值，显示这些核特征近似可以提高线性分类的准确性。在典型的应用场景中， n_components 应该大于输入表示中的特征数量，以便在线性分类方面取得改进。根据经验法则，评估得分/运行时间成本的最佳值通常在 n_components = 10 * n_features 左右，尽管这可能取决于处理的具体数据集。请注意，由于原始样本有 54 个特征，四次多项式核的显式特征映射将有大约 850 万个特征（准确地说是 54^4）。感谢 PolynomialCountSketch ，我们可以将该特征空间的大部分判别信息浓缩成一个更紧凑的表示。虽然在这个例子中我们只运行了一次实验（ n_runs = 1），但在实际操作中，应多次重复实验以补偿 PolynomialCountSketch 的随机性。

from sklearn.kernel_approximation import PolynomialCountSketch

n_runs = 1
N_COMPONENTS = [250, 500, 1000, 2000]

for n_components in N_COMPONENTS:
    ps_lsvm_time = 0
    ps_lsvm_score = 0
    for _ in range(n_runs):
        pipeline = make_pipeline(
            PolynomialCountSketch(n_components=n_components, degree=4),
            LinearSVC(),
        )

        start = time.time()
        pipeline.fit(X_train, y_train)
        ps_lsvm_time += time.time() - start
        ps_lsvm_score += 100 * pipeline.score(X_test, y_test)

    ps_lsvm_time /= n_runs
    ps_lsvm_score /= n_runs

    results[f"LSVM + PS({n_components})"] = {
        "time": ps_lsvm_time,
        "score": ps_lsvm_score,
    }
    print(
        f"Linear SVM score on {n_components} PolynomialCountSketch "
        + f"features: {ps_lsvm_score:.2f}%"
    )

Linear SVM score on 250 PolynomialCountSketch features: 76.02%
Linear SVM score on 500 PolynomialCountSketch features: 77.27%
Linear SVM score on 1000 PolynomialCountSketch features: 77.94%
Linear SVM score on 2000 PolynomialCountSketch features: 78.25%

建立核化支持向量机模型#

训练一个核化支持向量机（SVM），以查看 PolynomialCountSketch 在多大程度上接近核的性能。当然，这可能需要一些时间，因为 SVC 类的扩展性相对较差。这也是为什么核近似器如此有用的原因：

from sklearn.svm import SVC

ksvm = SVC(C=500.0, kernel="poly", degree=4, coef0=0, gamma=1.0)

start = time.time()
ksvm.fit(X_train, y_train)
ksvm_time = time.time() - start
ksvm_score = 100 * ksvm.score(X_test, y_test)

results["KSVM"] = {"time": ksvm_time, "score": ksvm_score}
print(f"Kernel-SVM score on raw features: {ksvm_score:.2f}%")

Kernel-SVM score on raw features: 79.78%

比较结果#

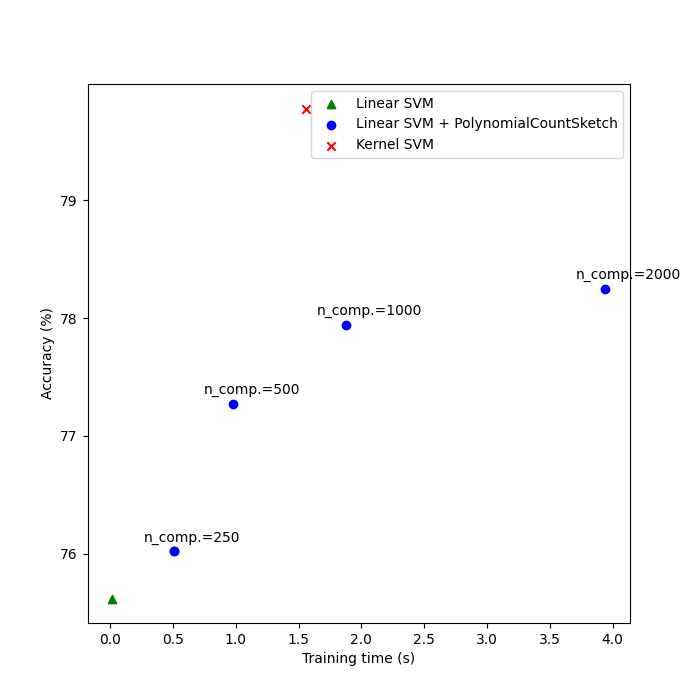
最后，将不同方法的结果与它们的训练时间进行对比绘图。正如我们所见，核化SVM达到了更高的准确率，但其训练时间要长得多，而且最重要的是，如果训练样本数量增加，其训练时间将增长得更快。

import matplotlib.pyplot as plt

fig, ax = plt.subplots(figsize=(7, 7))
ax.scatter(
    [
        results["LSVM"]["time"],
    ],
    [
        results["LSVM"]["score"],
    ],
    label="Linear SVM",
    c="green",
    marker="^",
)

ax.scatter(
    [
        results["LSVM + PS(250)"]["time"],
    ],
    [
        results["LSVM + PS(250)"]["score"],
    ],
    label="Linear SVM + PolynomialCountSketch",
    c="blue",
)

for n_components in N_COMPONENTS:
    ax.scatter(
        [
            results[f"LSVM + PS({n_components})"]["time"],
        ],
        [
            results[f"LSVM + PS({n_components})"]["score"],
        ],
        c="blue",
    )
    ax.annotate(
        f"n_comp.={n_components}",
        (
            results[f"LSVM + PS({n_components})"]["time"],
            results[f"LSVM + PS({n_components})"]["score"],
        ),
        xytext=(-30, 10),
        textcoords="offset pixels",
    )

ax.scatter(
    [
        results["KSVM"]["time"],
    ],
    [
        results["KSVM"]["score"],
    ],
    label="Kernel SVM",
    c="red",
    marker="x",
)

ax.set_xlabel("Training time (s)")
ax.set_ylabel("Accuracy (%)")
ax.legend()
plt.show()