Note

Go to the end to download the full example code. or to run this example in your browser via Binder

阈值变化对自训练的影响#

本示例说明了阈值变化对自训练的影响。加载 breast_cancer 数据集，并删除标签，使得569个样本中只有50个有标签。在这个数据集上，使用不同阈值拟合 SelfTrainingClassifier 。

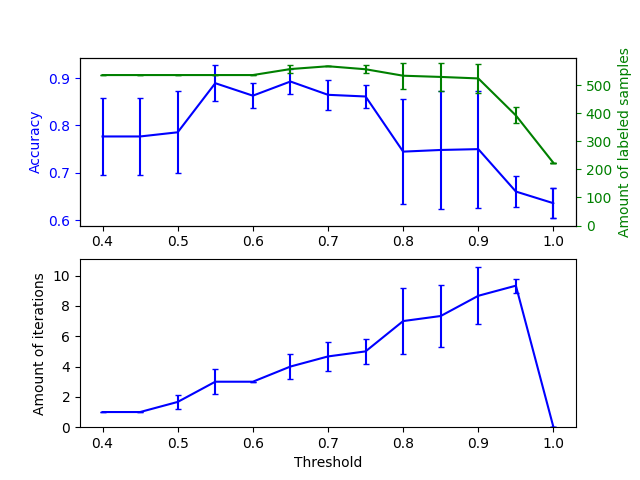
上图显示了分类器在拟合结束时可用的标记样本数量和分类器的准确性。下图显示了最后一次迭代中标记样本的情况。所有值都通过3折交叉验证。

在低阈值（在 [0.4, 0.5] 范围内）时，分类器从低置信度标记的样本中学习。这些低置信度样本可能有错误的预测标签，结果是基于这些错误标签的拟合产生了较差的准确性。注意，分类器几乎标记了所有样本，并且只需要一次迭代。

对于非常高的阈值（在 [0.9, 1) 范围内），我们观察到分类器没有扩充其数据集（自标记样本的数量为0）。因此，使用0.9999阈值所达到的准确性与普通监督分类器所能达到的准确性相同。

最佳准确性位于这两个极端之间，阈值大约在0.7。

# 作者：scikit-learn 开发者
# SPDX-License-Identifier: BSD-3-Clause

import matplotlib.pyplot as plt
import numpy as np

from sklearn import datasets
from sklearn.metrics import accuracy_score
from sklearn.model_selection import StratifiedKFold
from sklearn.semi_supervised import SelfTrainingClassifier
from sklearn.svm import SVC
from sklearn.utils import shuffle

n_splits = 3

X, y = datasets.load_breast_cancer(return_X_y=True)
X, y = shuffle(X, y, random_state=42)
y_true = y.copy()
y[50:] = -1
total_samples = y.shape[0]

base_classifier = SVC(probability=True, gamma=0.001, random_state=42)

x_values = np.arange(0.4, 1.05, 0.05)
x_values = np.append(x_values, 0.99999)
scores = np.empty((x_values.shape[0], n_splits))
amount_labeled = np.empty((x_values.shape[0], n_splits))
amount_iterations = np.empty((x_values.shape[0], n_splits))

for i, threshold in enumerate(x_values):
    self_training_clf = SelfTrainingClassifier(base_classifier, threshold=threshold)

    # 我们需要手动交叉验证，以避免在计算准确率时将 -1 视为一个单独的类别。
    skfolds = StratifiedKFold(n_splits=n_splits)
    for fold, (train_index, test_index) in enumerate(skfolds.split(X, y)):
        X_train = X[train_index]
        y_train = y[train_index]
        X_test = X[test_index]
        y_test = y[test_index]
        y_test_true = y_true[test_index]

        self_training_clf.fit(X_train, y_train)

        # 在拟合结束时标记样本的数量
        amount_labeled[i, fold] = (
            total_samples
            - np.unique(self_training_clf.labeled_iter_, return_counts=True)[1][0]
        )
        # 分类器标记样本的最后一次迭代
        amount_iterations[i, fold] = np.max(self_training_clf.labeled_iter_)

        y_pred = self_training_clf.predict(X_test)
        scores[i, fold] = accuracy_score(y_test_true, y_pred)


ax1 = plt.subplot(211)
ax1.errorbar(
    x_values, scores.mean(axis=1), yerr=scores.std(axis=1), capsize=2, color="b"
)
ax1.set_ylabel("Accuracy", color="b")
ax1.tick_params("y", colors="b")

ax2 = ax1.twinx()
ax2.errorbar(
    x_values,
    amount_labeled.mean(axis=1),
    yerr=amount_labeled.std(axis=1),
    capsize=2,
    color="g",
)
ax2.set_ylim(bottom=0)
ax2.set_ylabel("Amount of labeled samples", color="g")
ax2.tick_params("y", colors="g")

ax3 = plt.subplot(212, sharex=ax1)
ax3.errorbar(
    x_values,
    amount_iterations.mean(axis=1),
    yerr=amount_iterations.std(axis=1),
    capsize=2,
    color="b",
)
ax3.set_ylim(bottom=0)
ax3.set_ylabel("Amount of iterations")
ax3.set_xlabel("Threshold")

plt.show()