Note

Go to the end to download the full example code. or to run this example in your browser via Binder

训练误差与测试误差#

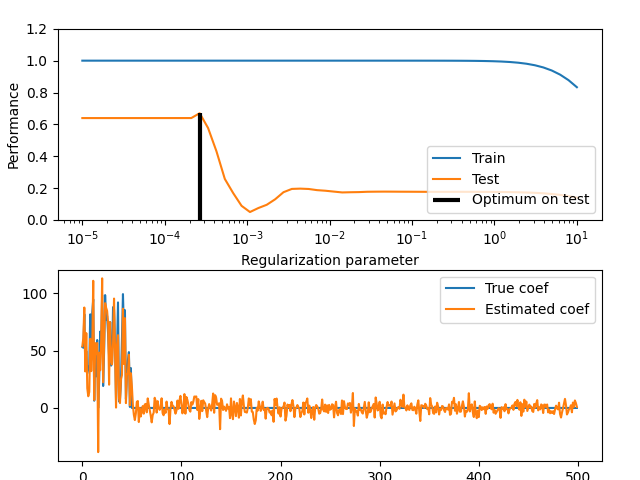
说明估计器在未见数据（测试数据）上的表现与在训练数据上的表现不同。随着正则化的增加，训练数据上的表现会下降，而测试数据上的表现会在正则化参数的某个范围内达到最佳。示例使用弹性网络回归模型，性能通过解释方差（即R^2）来衡量。

# 作者：scikit-learn 开发者
# SPDX-License-Identifier: BSD-3-Clause

生成示例数据#

import numpy as np

from sklearn import linear_model
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split

n_samples_train, n_samples_test, n_features = 75, 150, 500
X, y, coef = make_regression(
    n_samples=n_samples_train + n_samples_test,
    n_features=n_features,
    n_informative=50,
    shuffle=False,
    noise=1.0,
    coef=True,
)
X_train, X_test, y_train, y_test = train_test_split(
    X, y, train_size=n_samples_train, test_size=n_samples_test, shuffle=False
)

计算训练和测试误差#

alphas = np.logspace(-5, 1, 60)
enet = linear_model.ElasticNet(l1_ratio=0.7, max_iter=10000)
train_errors = list()
test_errors = list()
for alpha in alphas:
    enet.set_params(alpha=alpha)
    enet.fit(X_train, y_train)
    train_errors.append(enet.score(X_train, y_train))
    test_errors.append(enet.score(X_test, y_test))

i_alpha_optim = np.argmax(test_errors)
alpha_optim = alphas[i_alpha_optim]
print("Optimal regularization parameter : %s" % alpha_optim)

# 估计在最优正则化参数下的全数据 coef_
enet.set_params(alpha=alpha_optim)
coef_ = enet.fit(X, y).coef_

Optimal regularization parameter : 0.00026529484644318975

绘制结果函数#

import matplotlib.pyplot as plt

plt.subplot(2, 1, 1)
plt.semilogx(alphas, train_errors, label="Train")
plt.semilogx(alphas, test_errors, label="Test")
plt.vlines(
    alpha_optim,
    plt.ylim()[0],
    np.max(test_errors),
    color="k",
    linewidth=3,
    label="Optimum on test",
)
plt.legend(loc="lower right")
plt.ylim([0, 1.2])
plt.xlabel("Regularization parameter")
plt.ylabel("Performance")

# 显示估计的系数与真实系数的对比
plt.subplot(2, 1, 2)
plt.plot(coef, label="True coef")
plt.plot(coef_, label="Estimated coef")
plt.legend()
plt.subplots_adjust(0.09, 0.04, 0.94, 0.94, 0.26, 0.26)
plt.show()