分位数回归

此示例说明了分位数回归如何预测非平凡的条件分位数。

左图显示了误差分布为正态分布但具有非恒定方差（即异方差性）的情况。

右图显示了一个不对称误差分布的示例，即帕累托分布。

# 作者：scikit-learn 开发者
# SPDX-License-Identifier: BSD-3-Clause

数据集生成

为了说明分位数回归的行为，我们将生成两个合成数据集。这两个数据集的真实生成随机过程将由相同的期望值组成，并与单个特征 x 存在线性关系。

import numpy as np

rng = np.random.RandomState(42)
x = np.linspace(start=0, stop=10, num=100)
X = x[:, np.newaxis]
y_true_mean = 10 + 0.5 * x

我们将通过改变目标 y 的分布来创建两个后续问题，同时保持相同的期望值：

• 在第一种情况下，添加了异方差正态噪声；

• 在第二种情况下，添加了非对称帕累托噪声。

y_normal = y_true_mean + rng.normal(loc=0, scale=0.5 + 0.5 * x, size=x.shape[0])
a = 5
y_pareto = y_true_mean + 10 * (rng.pareto(a, size=x.shape[0]) - 1 / (a - 1))

让我们首先可视化数据集以及残差 y - mean(y) 的分布。

import matplotlib.pyplot as plt

_, axs = plt.subplots(nrows=2, ncols=2, figsize=(15, 11), sharex="row", sharey="row")

axs[0, 0].plot(x, y_true_mean, label="True mean")
axs[0, 0].scatter(x, y_normal, color="black", alpha=0.5, label="Observations")
axs[1, 0].hist(y_true_mean - y_normal, edgecolor="black")


axs[0, 1].plot(x, y_true_mean, label="True mean")
axs[0, 1].scatter(x, y_pareto, color="black", alpha=0.5, label="Observations")
axs[1, 1].hist(y_true_mean - y_pareto, edgecolor="black")

axs[0, 0].set_title("Dataset with heteroscedastic Normal distributed targets")
axs[0, 1].set_title("Dataset with asymmetric Pareto distributed target")
axs[1, 0].set_title(
    "Residuals distribution for heteroscedastic Normal distributed targets"
)
axs[1, 1].set_title("Residuals distribution for asymmetric Pareto distributed target")
axs[0, 0].legend()
axs[0, 1].legend()
axs[0, 0].set_ylabel("y")
axs[1, 0].set_ylabel("Counts")
axs[0, 1].set_xlabel("x")
axs[0, 0].set_xlabel("x")
axs[1, 0].set_xlabel("Residuals")
_ = axs[1, 1].set_xlabel("Residuals")

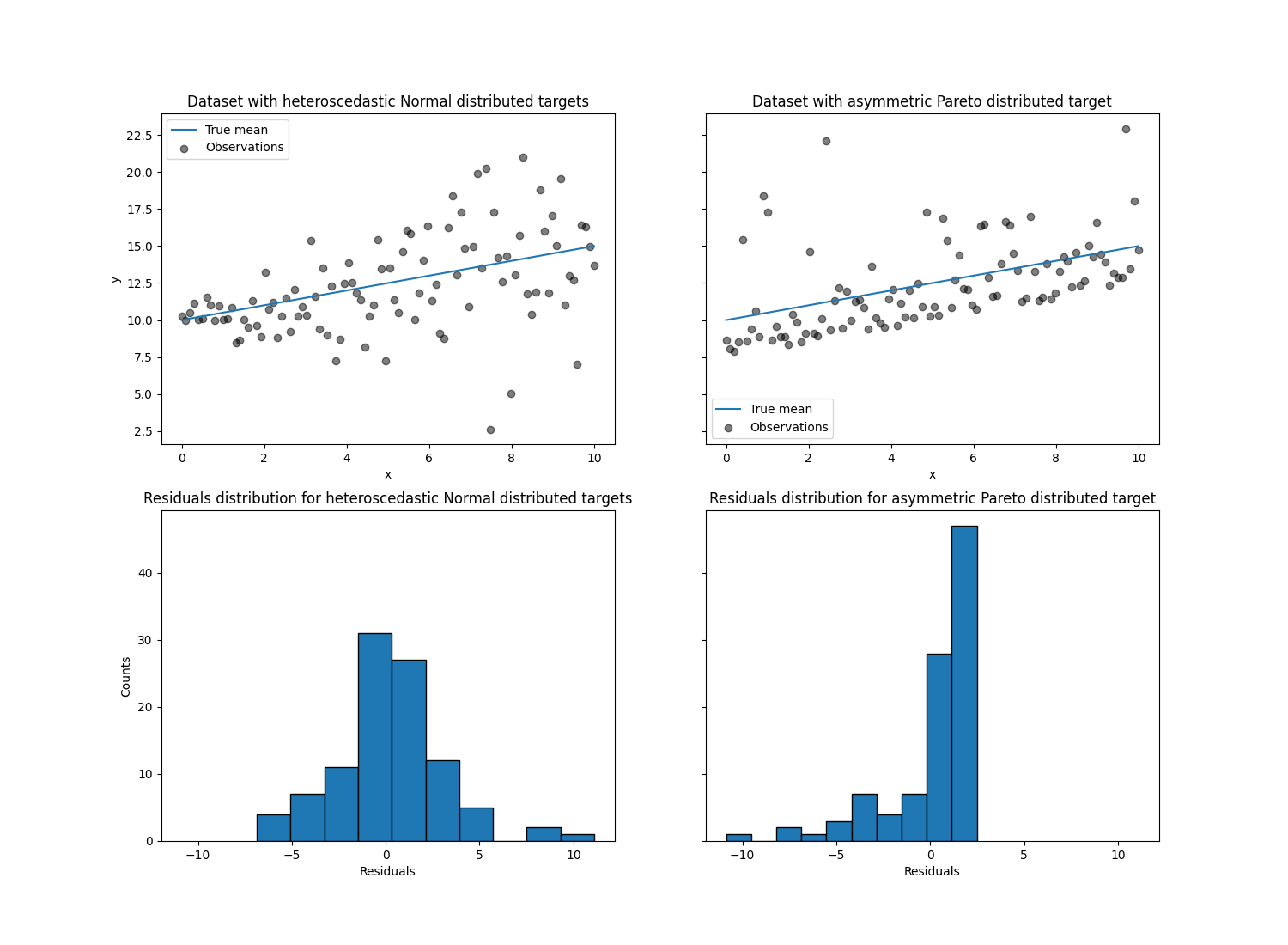
对于异方差正态分布的目标，我们观察到当特征 x 的值增加时，噪声的方差也在增加。

对于不对称的帕累托分布目标，我们观察到正残差是有界的。

这些类型的噪声目标使得通过:class:~sklearn.linear_model.LinearRegression 进行估计的效率降低，即我们需要更多的数据才能获得稳定的结果，此外，大的异常值会对拟合系数产生巨大影响。（换句话说：在方差恒定的情况下，普通最小二乘估计量随着样本量的增加会更快地收敛到*真实*系数。）

在这种不对称的情况下，中位数或不同的分位数可以提供额外的见解。此外，中位数估计对异常值和重尾分布更加稳健。但请注意，极端分位数是由非常少的数据点估计的。95%分位数大致由5%最大值估计，因此对异常值也有些敏感。

在本教程的剩余部分中，我们将展示如何在实践中使用 QuantileRegressor ，并提供对拟合模型属性的直观理解。最后，我们将比较 QuantileRegressor 和 LinearRegression 。

拟合 QuantileRegressor

在本节中，我们希望估计条件中位数以及固定在5%和95%的低分位数和高分位数。因此，我们将得到三个线性模型，每个分位数对应一个模型。

我们将使用5%和95%的分位数来查找训练样本中超出中心90%区间的异常值。

from sklearn.utils.fixes import parse_version, sp_version

# 这是为了避免旧版本的SciPy不兼容。如果使用较新版本的SciPy，你应该使用 `solver="highs"` 。
solver = "highs" if sp_version >= parse_version("1.6.0") else "interior-point"

from sklearn.linear_model import QuantileRegressor

quantiles = [0.05, 0.5, 0.95]
predictions = {}
out_bounds_predictions = np.zeros_like(y_true_mean, dtype=np.bool_)
for quantile in quantiles:
    qr = QuantileRegressor(quantile=quantile, alpha=0, solver=solver)
    y_pred = qr.fit(X, y_normal).predict(X)
    predictions[quantile] = y_pred

    if quantile == min(quantiles):
        out_bounds_predictions = np.logical_or(
            out_bounds_predictions, y_pred >= y_normal
        )
    elif quantile == max(quantiles):
        out_bounds_predictions = np.logical_or(
            out_bounds_predictions, y_pred <= y_normal
        )

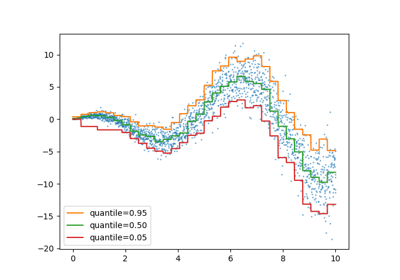
现在，我们可以绘制三个线性模型，并区分出在中心90%区间内的样本和在该区间外的样本。

plt.plot(X, y_true_mean, color="black", linestyle="dashed", label="True mean")

for quantile, y_pred in predictions.items():
    plt.plot(X, y_pred, label=f"Quantile: {quantile}")

plt.scatter(
    x[out_bounds_predictions],
    y_normal[out_bounds_predictions],
    color="black",
    marker="+",
    alpha=0.5,
    label="Outside interval",
)
plt.scatter(
    x[~out_bounds_predictions],
    y_normal[~out_bounds_predictions],
    color="black",
    alpha=0.5,
    label="Inside interval",
)

plt.legend()
plt.xlabel("x")
plt.ylabel("y")
_ = plt.title("Quantiles of heteroscedastic Normal distributed target")

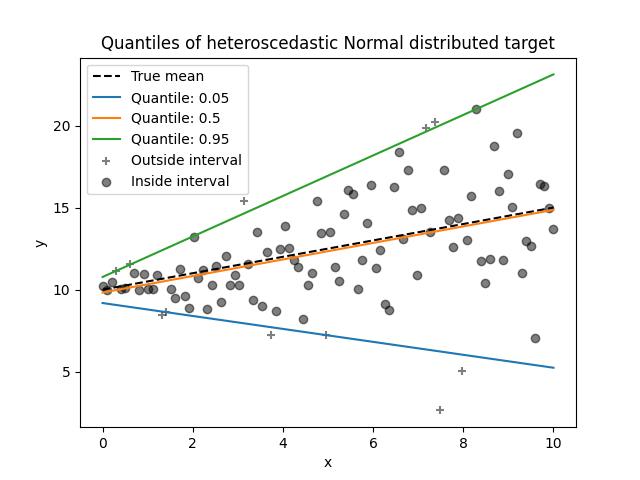
由于噪声仍然是正态分布的，特别是对称的，真实条件均值和真实条件中位数是一致的。实际上，我们看到估计的中位数几乎与真实均值相符。我们观察到噪声方差增加对5%和95%分位数的影响：这些分位数的斜率非常不同，并且随着 x 的增加，它们之间的区间变得更宽。

为了更直观地理解5%和95%分位数估计量的含义，可以计算在预测分位数（在上图中用叉号表示）之上和之下的样本数量，假设我们总共有100个样本。

我们可以使用非对称帕累托分布目标重复相同的实验。

quantiles = [0.05, 0.5, 0.95]
predictions = {}
out_bounds_predictions = np.zeros_like(y_true_mean, dtype=np.bool_)
for quantile in quantiles:
    qr = QuantileRegressor(quantile=quantile, alpha=0, solver=solver)
    y_pred = qr.fit(X, y_pareto).predict(X)
    predictions[quantile] = y_pred

    if quantile == min(quantiles):
        out_bounds_predictions = np.logical_or(
            out_bounds_predictions, y_pred >= y_pareto
        )
    elif quantile == max(quantiles):
        out_bounds_predictions = np.logical_or(
            out_bounds_predictions, y_pred <= y_pareto
        )

plt.plot(X, y_true_mean, color="black", linestyle="dashed", label="True mean")

for quantile, y_pred in predictions.items():
    plt.plot(X, y_pred, label=f"Quantile: {quantile}")

plt.scatter(
    x[out_bounds_predictions],
    y_pareto[out_bounds_predictions],
    color="black",
    marker="+",
    alpha=0.5,
    label="Outside interval",
)
plt.scatter(
    x[~out_bounds_predictions],
    y_pareto[~out_bounds_predictions],
    color="black",
    alpha=0.5,
    label="Inside interval",
)

plt.legend()
plt.xlabel("x")
plt.ylabel("y")
_ = plt.title("Quantiles of asymmetric Pareto distributed target")

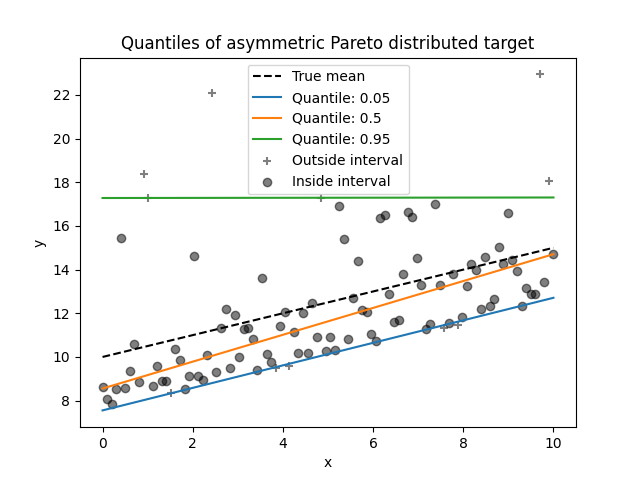
由于噪声分布的不对称性，我们观察到真实均值和估计的条件中位数是不同的。我们还观察到每个分位数模型都有不同的参数，以更好地拟合所需的分位数。请注意，理想情况下，所有分位数在这种情况下应该是平行的，这在数据点更多或分位数不那么极端时（例如10%和90%）会更加明显。

比较 QuantileRegressor 和 LinearRegression

在本节中，我们将详细讨论 QuantileRegressor 和 LinearRegression 所最小化的误差之间的差异。

实际上，LinearRegression 是一种最小二乘法，旨在最小化训练目标和预测目标之间的均方误差（MSE）。相比之下， quantile=0.5 的 QuantileRegressor 则是最小化平均绝对误差（MAE）。

让我们首先计算这些模型的训练误差，包括均方误差和平均绝对误差。我们将使用不对称的帕累托分布目标来使其更有趣，因为均值和中位数不相等。

from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_absolute_error, mean_squared_error

linear_regression = LinearRegression()
quantile_regression = QuantileRegressor(quantile=0.5, alpha=0, solver=solver)

y_pred_lr = linear_regression.fit(X, y_pareto).predict(X)
y_pred_qr = quantile_regression.fit(X, y_pareto).predict(X)

print(
    f"""Training error (in-sample performance)
    {linear_regression.__class__.__name__}:
    MAE = {mean_absolute_error(y_pareto, y_pred_lr):.3f}
    MSE = {mean_squared_error(y_pareto, y_pred_lr):.3f}
    {quantile_regression.__class__.__name__}:
    MAE = {mean_absolute_error(y_pareto, y_pred_qr):.3f}
    MSE = {mean_squared_error(y_pareto, y_pred_qr):.3f}
    """
)

Training error (in-sample performance)
    LinearRegression:
    MAE = 1.805
    MSE = 6.486
    QuantileRegressor:
    MAE = 1.670
    MSE = 7.025

在训练集上，我们看到 QuantileRegressor 的 MAE 低于 LinearRegression 。与此相反，LinearRegression 的 MSE 低于 QuantileRegressor 。这些结果证实了 MAE 是 QuantileRegressor 最小化的损失，而 MSE 是 LinearRegression 最小化的损失。

我们可以通过查看通过交叉验证获得的测试误差来进行类似的评估。

from sklearn.model_selection import cross_validate

cv_results_lr = cross_validate(
    linear_regression,
    X,
    y_pareto,
    cv=3,
    scoring=["neg_mean_absolute_error", "neg_mean_squared_error"],
)
cv_results_qr = cross_validate(
    quantile_regression,
    X,
    y_pareto,
    cv=3,
    scoring=["neg_mean_absolute_error", "neg_mean_squared_error"],
)
print(
    f"""Test error (cross-validated performance)
    {linear_regression.__class__.__name__}:
    MAE = {-cv_results_lr["test_neg_mean_absolute_error"].mean():.3f}
    MSE = {-cv_results_lr["test_neg_mean_squared_error"].mean():.3f}
    {quantile_regression.__class__.__name__}:
    MAE = {-cv_results_qr["test_neg_mean_absolute_error"].mean():.3f}
    MSE = {-cv_results_qr["test_neg_mean_squared_error"].mean():.3f}
    """
)

Test error (cross-validated performance)
    LinearRegression:
    MAE = 1.732
    MSE = 6.690
    QuantileRegressor:
    MAE = 1.679
    MSE = 7.129

我们在样本外评估中得出了类似的结论。

Related examples

绘制交叉验证预测

绘制交叉验证预测

k-means 假设的演示

k-means 假设的演示

scikit-learn 1.1 版本发布亮点

scikit-learn 1.1 版本发布亮点

不同核函数下高斯过程的先验和后验示例

不同核函数下高斯过程的先验和后验示例