Note
Go to the end to download the full example code. or to run this example in your browser via Binder
核岭回归和支持向量回归的比较#
核岭回归(KRR)和支持向量回归(SVR)都通过使用核技巧来学习非线性函数,即它们在由相应核引导的空间中学习线性函数,这对应于原始空间中的非线性函数。它们在损失函数(岭损失与ε-不敏感损失)上有所不同。与SVR相比,KRR的拟合可以通过闭式解完成,并且对于中等规模的数据集通常更快。另一方面,所学习的模型是非稀疏的,因此在预测时比SVR更慢。
这个示例在一个人工数据集上展示了这两种方法,该数据集由一个正弦目标函数和每五个数据点添加的强噪声组成。
作者:scikit-learn 开发者 SPDX-License-Identifier: BSD-3-Clause
生成示例数据#
import numpy as np
rng = np.random.RandomState(42)
X = 5 * rng.rand(10000, 1)
y = np.sin(X).ravel()
# 添加噪声到目标
y[::5] += 3 * (0.5 - rng.rand(X.shape[0] // 5))
X_plot = np.linspace(0, 5, 100000)[:, None]
构建基于核的回归模型#
from sklearn.kernel_ridge import KernelRidge
from sklearn.model_selection import GridSearchCV
from sklearn.svm import SVR
train_size = 100
svr = GridSearchCV(
SVR(kernel="rbf", gamma=0.1),
param_grid={"C": [1e0, 1e1, 1e2, 1e3], "gamma": np.logspace(-2, 2, 5)},
)
kr = GridSearchCV(
KernelRidge(kernel="rbf", gamma=0.1),
param_grid={"alpha": [1e0, 0.1, 1e-2, 1e-3], "gamma": np.logspace(-2, 2, 5)},
)
比较SVR和核岭回归的时间#
import time
t0 = time.time()
svr.fit(X[:train_size], y[:train_size])
svr_fit = time.time() - t0
print(f"Best SVR with params: {svr.best_params_} and R2 score: {svr.best_score_:.3f}")
print("SVR complexity and bandwidth selected and model fitted in %.3f s" % svr_fit)
t0 = time.time()
kr.fit(X[:train_size], y[:train_size])
kr_fit = time.time() - t0
print(f"Best KRR with params: {kr.best_params_} and R2 score: {kr.best_score_:.3f}")
print("KRR complexity and bandwidth selected and model fitted in %.3f s" % kr_fit)
sv_ratio = svr.best_estimator_.support_.shape[0] / train_size
print("Support vector ratio: %.3f" % sv_ratio)
t0 = time.time()
y_svr = svr.predict(X_plot)
svr_predict = time.time() - t0
print("SVR prediction for %d inputs in %.3f s" % (X_plot.shape[0], svr_predict))
t0 = time.time()
y_kr = kr.predict(X_plot)
kr_predict = time.time() - t0
print("KRR prediction for %d inputs in %.3f s" % (X_plot.shape[0], kr_predict))
Best SVR with params: {'C': 1.0, 'gamma': np.float64(0.1)} and R2 score: 0.737
SVR complexity and bandwidth selected and model fitted in 0.266 s
Best KRR with params: {'alpha': 0.1, 'gamma': np.float64(0.1)} and R2 score: 0.723
KRR complexity and bandwidth selected and model fitted in 0.076 s
Support vector ratio: 0.340
SVR prediction for 100000 inputs in 0.060 s
KRR prediction for 100000 inputs in 0.066 s
查看结果#
import matplotlib.pyplot as plt
sv_ind = svr.best_estimator_.support_
plt.scatter(
X[sv_ind],
y[sv_ind],
c="r",
s=50,
label="SVR support vectors",
zorder=2,
edgecolors=(0, 0, 0),
)
plt.scatter(X[:100], y[:100], c="k", label="data", zorder=1, edgecolors=(0, 0, 0))
plt.plot(
X_plot,
y_svr,
c="r",
label="SVR (fit: %.3fs, predict: %.3fs)" % (svr_fit, svr_predict),
)
plt.plot(
X_plot, y_kr, c="g", label="KRR (fit: %.3fs, predict: %.3fs)" % (kr_fit, kr_predict)
)
plt.xlabel("data")
plt.ylabel("target")
plt.title("SVR versus Kernel Ridge")
_ = plt.legend()
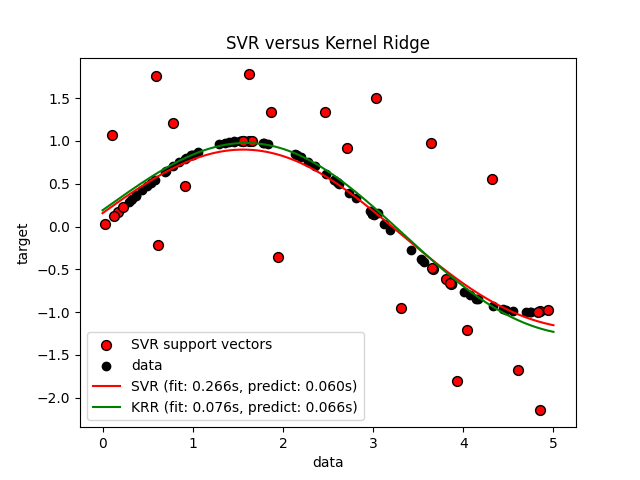
前面的图比较了在使用网格搜索优化RBF核的复杂度/正则化和带宽时,KRR和SVR的学习模型。学习到的函数非常相似;然而,拟合KRR的速度大约是拟合SVR(均使用网格搜索)的3-4倍。
理论上,预测100000个目标值时,SVR可能会快大约三倍,因为它仅使用大约1/3的训练数据点作为支持向量学习了一个稀疏模型。然而,实际上,由于每个模型计算核函数的实现细节,KRR模型可能同样快甚至更快,尽管它需要进行更多的算术运算。
可视化训练和预测时间#
plt.figure()
sizes = np.logspace(1, 3.8, 7).astype(int)
for name, estimator in {
"KRR": KernelRidge(kernel="rbf", alpha=0.01, gamma=10),
"SVR": SVR(kernel="rbf", C=1e2, gamma=10),
}.items():
train_time = []
test_time = []
for train_test_size in sizes:
t0 = time.time()
estimator.fit(X[:train_test_size], y[:train_test_size])
train_time.append(time.time() - t0)
t0 = time.time()
estimator.predict(X_plot[:1000])
test_time.append(time.time() - t0)
plt.plot(
sizes,
train_time,
"o-",
color="r" if name == "SVR" else "g",
label="%s (train)" % name,
)
plt.plot(
sizes,
test_time,
"o--",
color="r" if name == "SVR" else "g",
label="%s (test)" % name,
)
plt.xscale("log")
plt.yscale("log")
plt.xlabel("Train size")
plt.ylabel("Time (seconds)")
plt.title("Execution Time")
_ = plt.legend(loc="best")
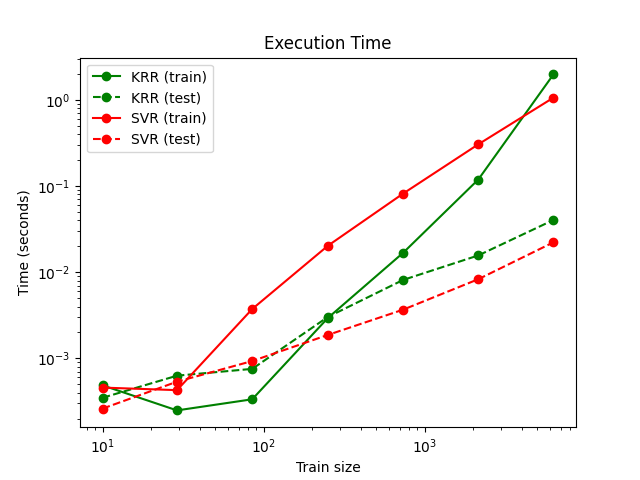
此图比较了KRR和SVR在不同训练集规模下的拟合和预测时间。对于中等规模的训练集(少于几千个样本),KRR的拟合速度比SVR快;然而,对于较大的训练集,SVR的扩展性更好。关于预测时间,由于学习到的稀疏解,SVR在所有训练集规模下都应该比KRR快,但由于实现细节,这在实际中不一定成立。请注意,稀疏度以及预测时间取决于SVR的参数epsilon和C。
可视化学习曲线#
from sklearn.model_selection import LearningCurveDisplay
_, ax = plt.subplots()
svr = SVR(kernel="rbf", C=1e1, gamma=0.1)
kr = KernelRidge(kernel="rbf", alpha=0.1, gamma=0.1)
common_params = {
"X": X[:100],
"y": y[:100],
"train_sizes": np.linspace(0.1, 1, 10),
"scoring": "neg_mean_squared_error",
"negate_score": True,
"score_name": "Mean Squared Error",
"score_type": "test",
"std_display_style": None,
"ax": ax,
}
LearningCurveDisplay.from_estimator(svr, **common_params)
LearningCurveDisplay.from_estimator(kr, **common_params)
ax.set_title("Learning curves")
ax.legend(handles=ax.get_legend_handles_labels()[0], labels=["SVR", "KRR"])
plt.show()
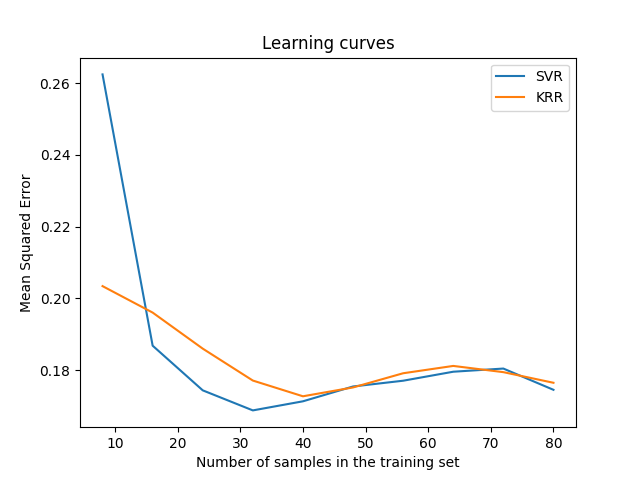
Total running time of the script: (0 minutes 4.494 seconds)
Related examples