Note

Go to the end to download the full example code. or to run this example in your browser via Binder

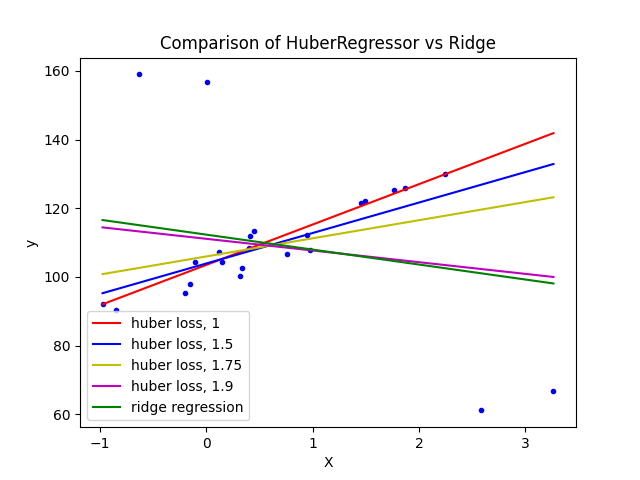
带有强异常值的数据集上的Huber回归与岭回归对比#

在带有异常值的数据集上拟合岭回归和Huber回归。

该示例显示了岭回归的预测结果受到数据集中存在的异常值的强烈影响。Huber回归器由于对这些异常值使用线性损失，因此受异常值的影响较小。随着Huber回归器的参数epsilon增加，其决策函数逐渐接近岭回归的决策函数。

# 作者：scikit-learn 开发者
# SPDX-License-Identifier：BSD-3-Clause

import matplotlib.pyplot as plt
import numpy as np

from sklearn.datasets import make_regression
from sklearn.linear_model import HuberRegressor, Ridge

# 生成玩具数据。
rng = np.random.RandomState(0)
X, y = make_regression(
    n_samples=20, n_features=1, random_state=0, noise=4.0, bias=100.0
)

# 向数据集中添加四个强烈的异常值。
X_outliers = rng.normal(0, 0.5, size=(4, 1))
y_outliers = rng.normal(0, 2.0, size=4)
X_outliers[:2, :] += X.max() + X.mean() / 4.0
X_outliers[2:, :] += X.min() - X.mean() / 4.0
y_outliers[:2] += y.min() - y.mean() / 4.0
y_outliers[2:] += y.max() + y.mean() / 4.0
X = np.vstack((X, X_outliers))
y = np.concatenate((y, y_outliers))
plt.plot(X, y, "b.")

# 拟合Huber回归器以适应一系列的epsilon值。
colors = ["r-", "b-", "y-", "m-"]

x = np.linspace(X.min(), X.max(), 7)
epsilon_values = [1, 1.5, 1.75, 1.9]
for k, epsilon in enumerate(epsilon_values):
    huber = HuberRegressor(alpha=0.0, epsilon=epsilon)
    huber.fit(X, y)
    coef_ = huber.coef_ * x + huber.intercept_
    plt.plot(x, coef_, colors[k], label="huber loss, %s" % epsilon)

# 拟合一个岭回归模型以将其与Huber回归模型进行比较。
ridge = Ridge(alpha=0.0, random_state=0)
ridge.fit(X, y)
coef_ridge = ridge.coef_
coef_ = ridge.coef_ * x + ridge.intercept_
plt.plot(x, coef_, "g-", label="ridge regression")

plt.title("Comparison of HuberRegressor vs Ridge")
plt.xlabel("X")
plt.ylabel("y")
plt.legend(loc=0)
plt.show()