Note
Go to the end to download the full example code. or to run this example in your browser via Binder
多类AdaBoost决策树#
本示例展示了提升算法如何提高多标签分类问题的预测准确性。它重现了Zhu等人[1]_图1所示的类似实验。
AdaBoost(自适应提升)的核心原理是对数据的重复重采样版本拟合一系列弱学习器(例如决策树)。每个样本都带有一个在每次训练步骤后调整的权重,以便对分类错误的样本分配更高的权重。带有替换的重采样过程考虑了分配给每个样本的权重。权重较高的样本在新数据集中被多次选中的机会更大,而权重较低的样本则不太可能被选中。这确保了算法的后续迭代集中于难以分类的样本。
参考文献
# Noel Dawe <noel.dawe@gmail.com>
# SPDX-License-Identifier: BSD-3-Clause
创建数据集#
分类数据集是通过采用十维标准正态分布(\(x\) 属于 \(R^{10}\) )并定义三个类来构建的,这些类由嵌套的同心十维球体分隔,使得每个类中的样本数量大致相等(\(\chi^2\) 分布的分位数)。
from sklearn.datasets import make_gaussian_quantiles
X, y = make_gaussian_quantiles(
n_samples=2_000, n_features=10, n_classes=3, random_state=1
)
我们将数据集分成两部分:70%的样本用于训练,剩下的30%用于测试。
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
X, y, train_size=0.7, random_state=42
)
训练 AdaBoostClassifier#
我们训练 AdaBoostClassifier 。该估计器利用提升方法来提高分类准确性。提升方法旨在训练弱学习器(即 estimator ),这些学习器从其前任的错误中学习。
在这里,我们将弱学习器定义为:class:~sklearn.tree.DecisionTreeClassifier ,并将最大叶子数设置为8。在实际情况下,这个参数应该进行调优。我们将其设置为一个相对较低的值,以限制示例的运行时间。
SAMME 算法内置于 AdaBoostClassifier 中,然后使用当前弱学习器做出的正确或错误预测来更新用于训练连续弱学习器的样本权重。此外,弱学习器本身的权重是根据其在分类训练样本中的准确性计算的。弱学习器的权重决定了其对最终集成预测的影响。
from sklearn.ensemble import AdaBoostClassifier
from sklearn.tree import DecisionTreeClassifier
weak_learner = DecisionTreeClassifier(max_leaf_nodes=8)
n_estimators = 300
adaboost_clf = AdaBoostClassifier(
estimator=weak_learner,
n_estimators=n_estimators,
algorithm="SAMME",
random_state=42,
).fit(X_train, y_train)
分析#
AdaBoostClassifier 的收敛性#
为了展示提升算法在提高准确性方面的有效性,我们评估了提升树的误分类错误,并与两个基准分数进行比较。第一个基准分数是从单个弱学习器(即 DecisionTreeClassifier )获得的 misclassification_error ,作为参考点。第二个基准分数是从 DummyClassifier 获得的,该分类器预测数据集中最常见的类别。
from sklearn.dummy import DummyClassifier
from sklearn.metrics import accuracy_score
dummy_clf = DummyClassifier()
def misclassification_error(y_true, y_pred):
return 1 - accuracy_score(y_true, y_pred)
weak_learners_misclassification_error = misclassification_error(
y_test, weak_learner.fit(X_train, y_train).predict(X_test)
)
dummy_classifiers_misclassification_error = misclassification_error(
y_test, dummy_clf.fit(X_train, y_train).predict(X_test)
)
print(
"DecisionTreeClassifier's misclassification_error: "
f"{weak_learners_misclassification_error:.3f}"
)
print(
"DummyClassifier's misclassification_error: "
f"{dummy_classifiers_misclassification_error:.3f}"
)
DecisionTreeClassifier's misclassification_error: 0.475
DummyClassifier's misclassification_error: 0.692
在训练 DecisionTreeClassifier 模型后,所达到的错误率超过了通过猜测最频繁的类别标签(如 DummyClassifier 所做的那样)所获得的预期值。
现在,我们计算每次提升迭代中加法模型(DecisionTreeClassifier )在测试集上的 误分类错误 ,即 1 - 准确率 ,以评估其性能。
我们使用 staged_predict 方法,该方法的迭代次数与拟合的估计器数量相同(即对应于 n_estimators )。在第 n 次迭代时,AdaBoost 的预测仅使用前 n 个弱学习器。我们将这些预测与真实预测 y_test 进行比较,从而得出在链中添加新弱学习器的好处(或没有好处)的结论。
我们绘制了不同阶段的误分类错误:
import matplotlib.pyplot as plt
import pandas as pd
boosting_errors = pd.DataFrame(
{
"Number of trees": range(1, n_estimators + 1),
"AdaBoost": [
misclassification_error(y_test, y_pred)
for y_pred in adaboost_clf.staged_predict(X_test)
],
}
).set_index("Number of trees")
ax = boosting_errors.plot()
ax.set_ylabel("Misclassification error on test set")
ax.set_title("Convergence of AdaBoost algorithm")
plt.plot(
[boosting_errors.index.min(), boosting_errors.index.max()],
[weak_learners_misclassification_error, weak_learners_misclassification_error],
color="tab:orange",
linestyle="dashed",
)
plt.plot(
[boosting_errors.index.min(), boosting_errors.index.max()],
[
dummy_classifiers_misclassification_error,
dummy_classifiers_misclassification_error,
],
color="c",
linestyle="dotted",
)
plt.legend(["AdaBoost", "DecisionTreeClassifier", "DummyClassifier"], loc=1)
plt.show()
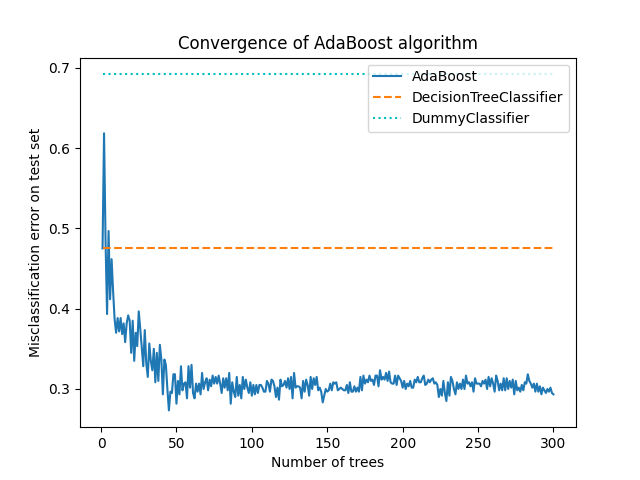
该图显示了每次提升迭代后测试集上的误分类错误。我们看到,提升树的错误在50次迭代后收敛到大约0.3的错误,表明与单棵树相比,准确率显著提高,如图中的虚线所示。
由于 SAMME 算法使用弱学习器的离散输出来训练提升模型,误分类误差会产生抖动。
AdaBoostClassifier 的收敛性主要受学习率(即 learning_rate )、使用的弱学习器数量( n_estimators )以及弱学习器的表达能力(例如 max_leaf_nodes )的影响。
弱学习器的错误率和权重#
如前所述,AdaBoost 是一种前向逐步加法模型。我们现在重点理解弱学习器的权重与其统计性能之间的关系。
我们使用拟合后的 AdaBoostClassifier 的属性 estimator_errors_ 和 estimator_weights_ 来研究这一联系。
weak_learners_info = pd.DataFrame(
{
"Number of trees": range(1, n_estimators + 1),
"Errors": adaboost_clf.estimator_errors_,
"Weights": adaboost_clf.estimator_weights_,
}
).set_index("Number of trees")
axs = weak_learners_info.plot(
subplots=True, layout=(1, 2), figsize=(10, 4), legend=False, color="tab:blue"
)
axs[0, 0].set_ylabel("Train error")
axs[0, 0].set_title("Weak learner's training error")
axs[0, 1].set_ylabel("Weight")
axs[0, 1].set_title("Weak learner's weight")
fig = axs[0, 0].get_figure()
fig.suptitle("Weak learner's errors and weights for the AdaBoostClassifier")
fig.tight_layout()
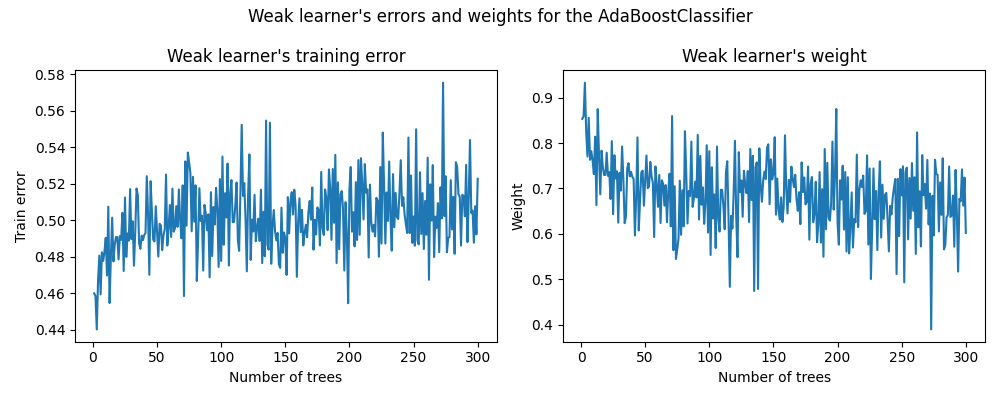
在左图中,我们展示了每次提升迭代中每个弱学习器在重新加权的训练集上的加权误差。在右图中,我们展示了每个弱学习器的权重,这些权重随后用于生成最终加性模型的预测。
我们看到弱学习器的误差是权重的倒数。这意味着我们的加法模型会通过增加其对最终决策的影响来更加信任在训练集上误差较小的弱学习器。实际上,这正是AdaBoost中每次迭代后更新基学习器权重的公式。
#Mathematical details
在阶段 \(m\) 训练的弱学习器的权重与其误分类误差成反比关系,如下所示:
其中 \(\alpha^{(m)}\) 和 \(err^{(m)}\) 分别是第 \(m\) 个弱分类器的权重和误差,\(K\) 是分类问题中的类别数量。
另一个有趣的观察结果归结为这样一个事实:模型的前几个弱学习器比提升链后面的弱学习器犯的错误更少。
这种观察背后的直觉如下:由于样本重加权,后面的分类器被迫尝试分类更困难或噪声较大的样本,并忽略已经分类良好的样本。因此,训练集上的总体误差将会增加。这就是为什么弱学习器的权重被构建来抵消表现较差的弱学习器的原因。
Total running time of the script: (0 minutes 7.525 seconds)
Related examples