Note

Go to the end to download the full example code. or to run this example in your browser via Binder

直方图梯度提升树的特性#

基于直方图的梯度提升 (HGBT) 模型可能是 scikit-learn 中最有用的监督学习模型之一。它们基于现代的梯度提升实现，可与 LightGBM 和 XGBoost 相媲美。因此，HGBT 模型比其他模型（如随机森林）具有更多的特性，并且通常表现更好，尤其是在样本数量超过几万时（参见 比较随机森林和直方图梯度提升模型 ）。

HGBT 模型的主要可用特性包括：

  1. 多种可用于均值和分位数回归任务的损失函数，参见 分位数损失 。

  2. 类别支持_gbdt ，参见 梯度提升中的类别特征支持 。

  3. 提前停止。

  4. nan支持_hgbt ，避免了对插补器的需求。

  5. 单调约束_gbdt 。

  6. 交互约束_hgbt 。

本示例旨在展示除第 2 点和第 6 点之外的所有特性在实际生活中的应用。

# 作者：scikit-learn 开发者
# SPDX-License-Identifier: BSD-3-Clause

准备数据#

electricity dataset 数据集包含从澳大利亚新南威尔士电力市场收集的数据。在这个市场中，价格不是固定的，而是受供需影响。价格每五分钟设定一次。与邻近的维多利亚州之间的电力传输是为了缓解波动。

该数据集原名ELEC2，包含45,312个实例，日期从1996年5月7日至1998年12月5日。数据集中的每个样本对应一个30分钟的时间段，即每一天有48个实例。数据集中的每个样本有7列：

  • 日期：1996年5月7日至1998年12月5日之间。归一化为0到1之间；

  • 星期几：星期几（1-7）；

  • 时间段：24小时内的半小时间隔。归一化为0到1之间；

  • nswprice/nswdemand：新南威尔士的电价/电力需求；

  • vicprice/vicdemand：维多利亚的电价/电力需求。

最初，这是一个分类任务，但在这里我们将其用于回归任务，以预测各州之间计划的电力传输。

from sklearn.datasets import fetch_openml

electricity = fetch_openml(
    name="electricity", version=1, as_frame=True, parser="pandas"
)
df = electricity.frame

这个特定数据集在前17,760个样本中具有逐步常数目标：

df["transfer"][:17_760].unique()

array([0.414912, 0.500526])

让我们删除这些条目，并探索一周中不同天的每小时电力传输情况：

import matplotlib.pyplot as plt
import seaborn as sns

df = electricity.frame.iloc[17_760:]
X = df.drop(columns=["transfer", "class"])
y = df["transfer"]

fig, ax = plt.subplots(figsize=(15, 10))
pointplot = sns.lineplot(x=df["period"], y=df["transfer"], hue=df["day"], ax=ax)
handles, lables = ax.get_legend_handles_labels()
ax.set(
    title="Hourly energy transfer for different days of the week",
    xlabel="Normalized time of the day",
    ylabel="Normalized energy transfer",
)
_ = ax.legend(handles, ["Sun", "Mon", "Tue", "Wed", "Thu", "Fri", "Sat"])
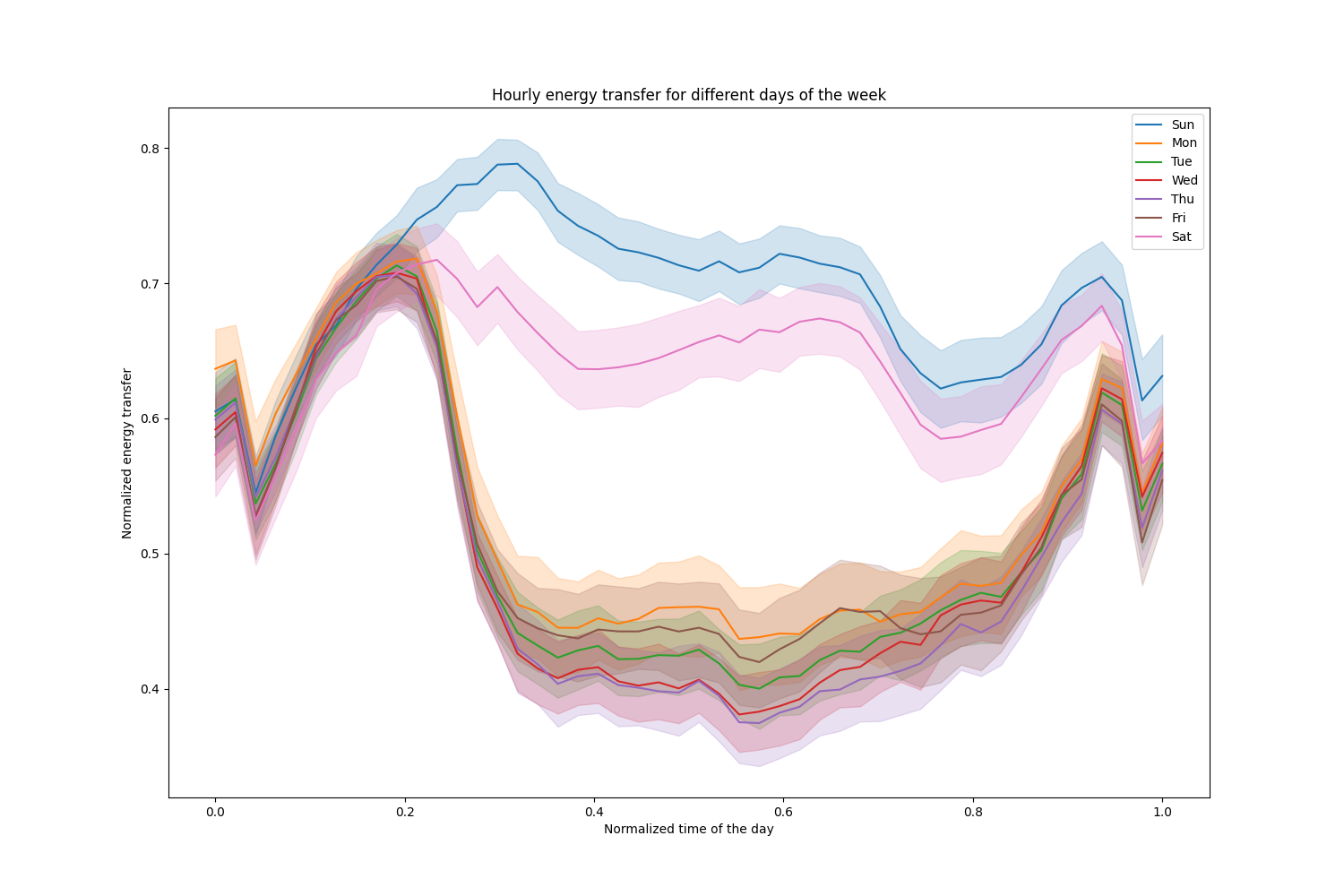
Hourly energy transfer for different days of the week

请注意，能量传递在周末期间系统性地增加。

树的数量和提前停止的效果#

为了说明（最大）树的数量的效果，我们使用整个数据集训练一个 HistGradientBoostingRegressor 来预测每日电力传输。然后我们根据 max_iter 参数可视化其预测结果。在这里，我们不尝试评估模型的性能及其泛化能力，而是其从训练数据中学习的能力。

from sklearn.ensemble import HistGradientBoostingRegressor
from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, shuffle=False)

print(f"Training sample size: {X_train.shape[0]}")
print(f"Test sample size: {X_test.shape[0]}")
print(f"Number of features: {X_train.shape[1]}")

Training sample size: 16531
Test sample size: 11021
Number of features: 7

max_iter_list = [5, 50]
average_week_demand = (
    df.loc[X_test.index].groupby(["day", "period"], observed=False)["transfer"].mean()
)
colors = sns.color_palette("colorblind")
fig, ax = plt.subplots(figsize=(10, 5))
average_week_demand.plot(color=colors[0], label="recorded average", linewidth=2, ax=ax)

for idx, max_iter in enumerate(max_iter_list):
    hgbt = HistGradientBoostingRegressor(
        max_iter=max_iter, categorical_features=None, random_state=42
    )
    hgbt.fit(X_train, y_train)

    y_pred = hgbt.predict(X_test)
    prediction_df = df.loc[X_test.index].copy()
    prediction_df["y_pred"] = y_pred
    average_pred = prediction_df.groupby(["day", "period"], observed=False)[
        "y_pred"
    ].mean()
    average_pred.plot(
        color=colors[idx + 1], label=f"max_iter={max_iter}", linewidth=2, ax=ax
    )

ax.set(
    title="Predicted average energy transfer during the week",
    xticks=[(i + 0.2) * 48 for i in range(7)],
    xticklabels=["Sun", "Mon", "Tue", "Wed", "Thu", "Fri", "Sat"],
    xlabel="Time of the week",
    ylabel="Normalized energy transfer",
)
_ = ax.legend()
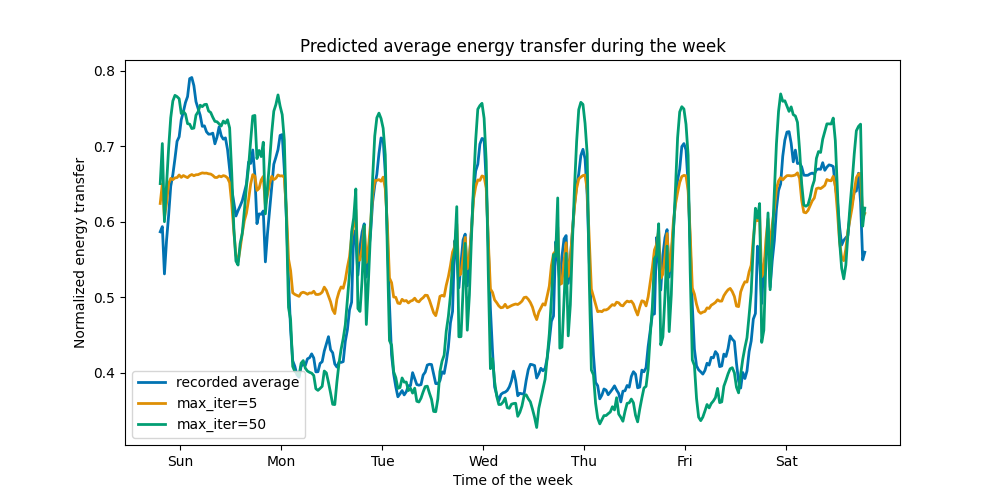
Predicted average energy transfer during the week

只需几次迭代，HGBT 模型就能收敛（参见 比较随机森林和直方图梯度提升模型 ），这意味着再增加树的数量也不会再提高模型的性能。在上图中，5 次迭代不足以得到良好的预测结果。而通过 50 次迭代，我们已经能够取得不错的效果。

将 max_iter 设置得过高可能会降低预测质量并消耗大量可避免的计算资源。因此，scikit-learn 中的 HGBT 实现提供了一种自动 提前停止 策略。使用该策略时，模型会使用一部分训练数据作为内部验证集（ validation_fraction ），如果验证分数在 n_iter_no_change 次迭代后没有提高（或降低）并超过一定容差（ tol ），则停止训练。

请注意， learning_rate 和 max_iter 之间存在权衡：通常，较小的学习率更可取，但需要更多的迭代才能收敛到最小损失，而较大的学习率收敛更快（需要的迭代/树更少），但代价是较大的最小损失。

由于学习率与迭代次数之间的高度相关性，一个好的做法是与所有（重要的）其他超参数一起调整学习率，在训练集上使用足够大的 max_iter 值拟合 HBGT，并通过早停和一些显式的 validation_fraction 来确定最佳的 max_iter 。

common_params = {
    "max_iter": 1_000,
    "learning_rate": 0.3,
    "validation_fraction": 0.2,
    "random_state": 42,
    "categorical_features": None,
    "scoring": "neg_root_mean_squared_error",
}

hgbt = HistGradientBoostingRegressor(early_stopping=True, **common_params)
hgbt.fit(X_train, y_train)

_, ax = plt.subplots()
plt.plot(-hgbt.validation_score_)
_ = ax.set(
    xlabel="number of iterations",
    ylabel="root mean squared error",
    title=f"Loss of hgbt with early stopping (n_iter={hgbt.n_iter_})",
)
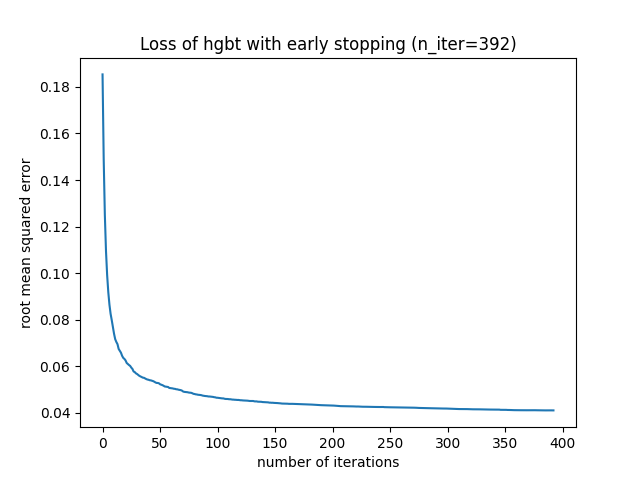
Loss of hgbt with early stopping (n_iter=392)

我们可以将 max_iter 的值覆盖为一个合理的值，从而避免内部验证的额外计算成本。将迭代次数取整可能会考虑到训练集的变异性：

import math

common_params["max_iter"] = math.ceil(hgbt.n_iter_ / 100) * 100
common_params["early_stopping"] = False
hgbt = HistGradientBoostingRegressor(**common_params)

Note

在早停期间进行的内部验证对于时间序列来说并不是最优的。

对缺失值的支持#

HGBT 模型原生支持缺失值。在训练过程中，树生成器会根据潜在增益决定每次分裂时带有缺失值的样本应该去往哪个子节点（左或右）。在预测时，这些样本会被相应地发送到学习到的子节点。如果某个特征在训练期间没有缺失值，那么在预测时，该特征有缺失值的样本会被发送到拥有最多样本的子节点（如在拟合期间所见）。

本示例展示了HGBT回归如何处理完全随机缺失（MCAR）的值，即缺失情况不依赖于观测数据或未观测数据。我们可以通过随机将某些特征的值替换为 nan 值来模拟这种情况。

import numpy as np

from sklearn.metrics import root_mean_squared_error

rng = np.random.RandomState(42)
first_week = slice(0, 336)  # first week in the test set as 7 * 48 = 336
missing_fraction_list = [0, 0.01, 0.03]


def generate_missing_values(X, missing_fraction):
    total_cells = X.shape[0] * X.shape[1]
    num_missing_cells = int(total_cells * missing_fraction)
    row_indices = rng.choice(X.shape[0], num_missing_cells, replace=True)
    col_indices = rng.choice(X.shape[1], num_missing_cells, replace=True)
    X_missing = X.copy()
    X_missing.iloc[row_indices, col_indices] = np.nan
    return X_missing


fig, ax = plt.subplots(figsize=(12, 6))
ax.plot(y_test.values[first_week], label="Actual transfer")

for missing_fraction in missing_fraction_list:
    X_train_missing = generate_missing_values(X_train, missing_fraction)
    X_test_missing = generate_missing_values(X_test, missing_fraction)
    hgbt.fit(X_train_missing, y_train)
    y_pred = hgbt.predict(X_test_missing[first_week])
    rmse = root_mean_squared_error(y_test[first_week], y_pred)
    ax.plot(
        y_pred[first_week],
        label=f"missing_fraction={missing_fraction}, RMSE={rmse:.3f}",
        alpha=0.5,
    )
ax.set(
    title="Daily energy transfer predictions on data with MCAR values",
    xticks=[(i + 0.2) * 48 for i in range(7)],
    xticklabels=["Mon", "Tue", "Wed", "Thu", "Fri", "Sat", "Sun"],
    xlabel="Time of the week",
    ylabel="Normalized energy transfer",
)
_ = ax.legend(loc="lower right")
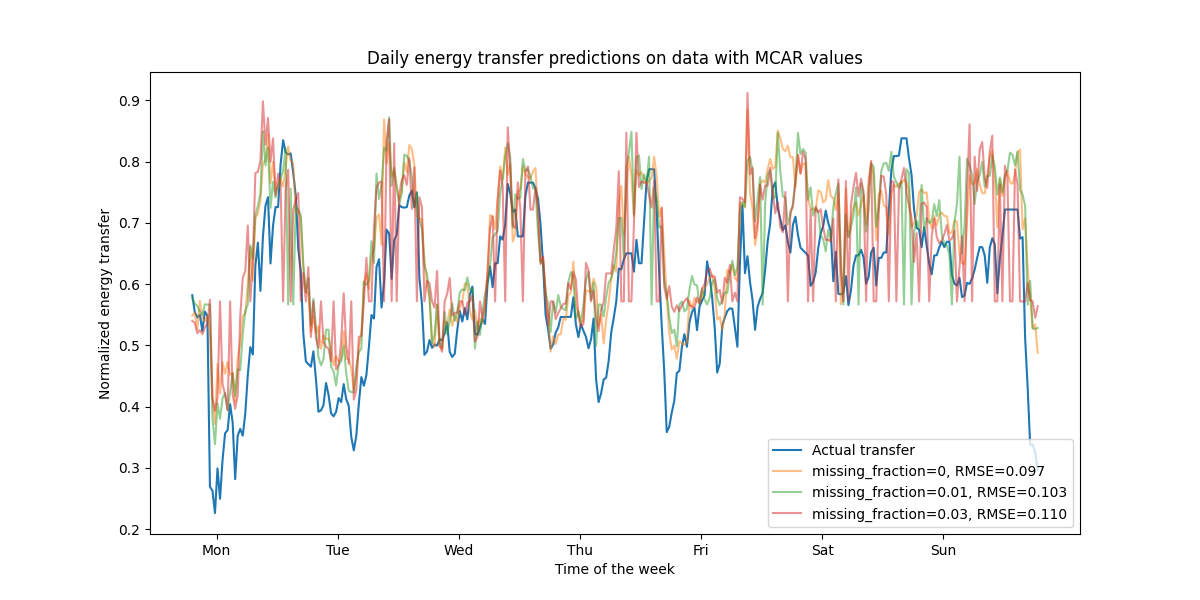
Daily energy transfer predictions on data with MCAR values

正如预期的那样，随着缺失值比例的增加，模型性能会下降。

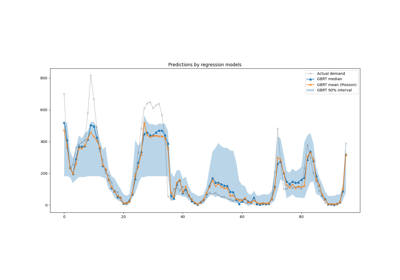
支持分位数损失#

在回归中，分位数损失使我们能够观察目标变量的变异性或不确定性。例如，预测第5和第95百分位数可以提供一个90%的预测区间，即我们期望新的观测值以90%的概率落在该区间内。

from sklearn.metrics import mean_pinball_loss

quantiles = [0.95, 0.05]
predictions = []

fig, ax = plt.subplots(figsize=(12, 6))
ax.plot(y_test.values[first_week], label="Actual transfer")

for quantile in quantiles:
    hgbt_quantile = HistGradientBoostingRegressor(
        loss="quantile", quantile=quantile, **common_params
    )
    hgbt_quantile.fit(X_train, y_train)
    y_pred = hgbt_quantile.predict(X_test[first_week])

    predictions.append(y_pred)
    score = mean_pinball_loss(y_test[first_week], y_pred)
    ax.plot(
        y_pred[first_week],
        label=f"quantile={quantile}, pinball loss={score:.2f}",
        alpha=0.5,
    )

ax.fill_between(
    range(len(predictions[0][first_week])),
    predictions[0][first_week],
    predictions[1][first_week],
    color=colors[0],
    alpha=0.1,
)
ax.set(
    title="Daily energy transfer predictions with quantile loss",
    xticks=[(i + 0.2) * 48 for i in range(7)],
    xticklabels=["Mon", "Tue", "Wed", "Thu", "Fri", "Sat", "Sun"],
    xlabel="Time of the week",
    ylabel="Normalized energy transfer",
)
_ = ax.legend(loc="lower right")
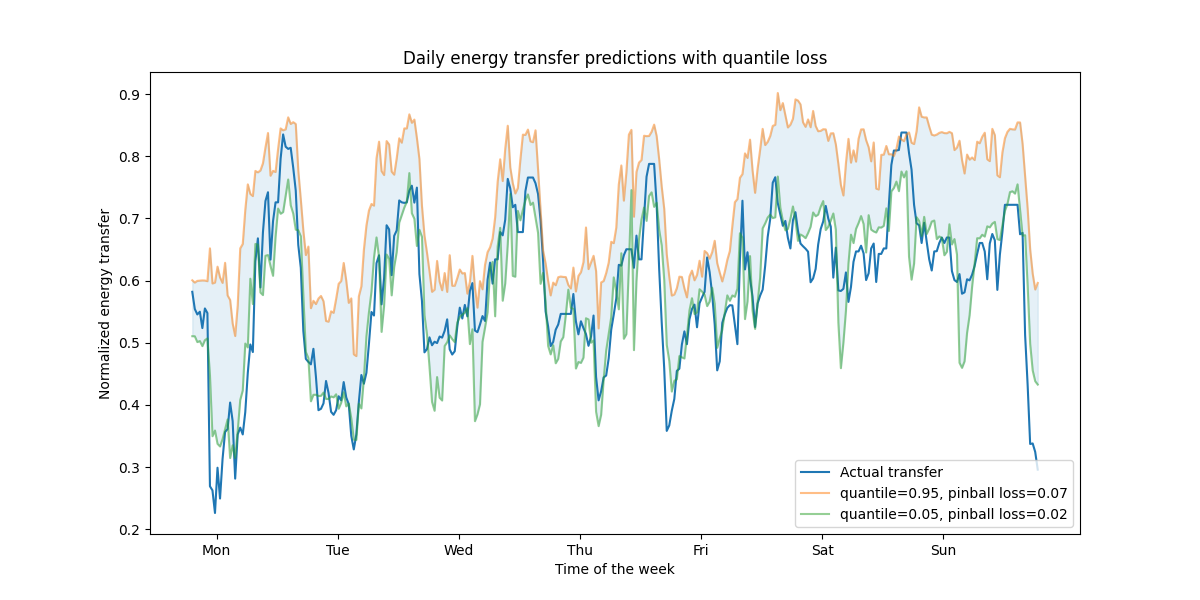
Daily energy transfer predictions with quantile loss

我们观察到一种高估能量传递的趋势。这可以通过计算经验覆盖数来定量确认，正如在:ref:置信区间校准部分 <calibration-section> 中所做的那样。请记住，这些预测的百分位数只是模型的估计值。仍然可以通过以下方式提高此类估计的质量：

单调约束#

在特定领域知识要求特征与目标之间的关系单调递增或递减的情况下，可以使用单调约束在HGBT模型的预测中强制执行这种行为。这使得模型更具可解释性，并且可以在增加偏差的风险下减少其方差（并可能减轻过拟合）。单调约束还可以用于强制执行特定的监管要求，确保合规并符合伦理考虑。

在当前示例中，从维多利亚向新南威尔士转移能源的政策旨在缓解价格波动，这意味着模型预测必须强制执行这一目标，即转移应随着新南威尔士的价格和需求增加而增加，但也应随着维多利亚的价格和需求增加而减少，以使两地居民都受益。

如果训练数据具有特征名称，可以通过传递一个符合以下约定的字典来指定单调约束：

  • 1：单调递增

  • 0：无约束

  • -1：单调递减

或者，可以传递一个类似数组的对象，通过位置编码上述约定。

from sklearn.inspection import PartialDependenceDisplay

monotonic_cst = {
    "date": 0,
    "day": 0,
    "period": 0,
    "nswdemand": 1,
    "nswprice": 1,
    "vicdemand": -1,
    "vicprice": -1,
}
hgbt_no_cst = HistGradientBoostingRegressor(
    categorical_features=None, random_state=42
).fit(X, y)
hgbt_cst = HistGradientBoostingRegressor(
    monotonic_cst=monotonic_cst, categorical_features=None, random_state=42
).fit(X, y)

fig, ax = plt.subplots(nrows=2, figsize=(15, 10))
disp = PartialDependenceDisplay.from_estimator(
    hgbt_no_cst,
    X,
    features=["nswdemand", "nswprice"],
    line_kw={"linewidth": 2, "label": "unconstrained", "color": "tab:blue"},
    ax=ax[0],
)
PartialDependenceDisplay.from_estimator(
    hgbt_cst,
    X,
    features=["nswdemand", "nswprice"],
    line_kw={"linewidth": 2, "label": "constrained", "color": "tab:orange"},
    ax=disp.axes_,
)
disp = PartialDependenceDisplay.from_estimator(
    hgbt_no_cst,
    X,
    features=["vicdemand", "vicprice"],
    line_kw={"linewidth": 2, "label": "unconstrained", "color": "tab:blue"},
    ax=ax[1],
)
PartialDependenceDisplay.from_estimator(
    hgbt_cst,
    X,
    features=["vicdemand", "vicprice"],
    line_kw={"linewidth": 2, "label": "constrained", "color": "tab:orange"},
    ax=disp.axes_,
)
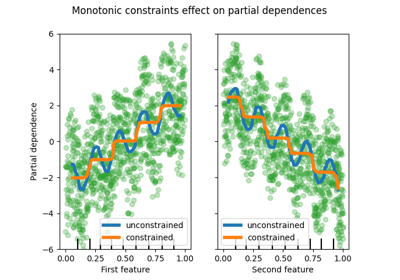
_ = plt.legend()
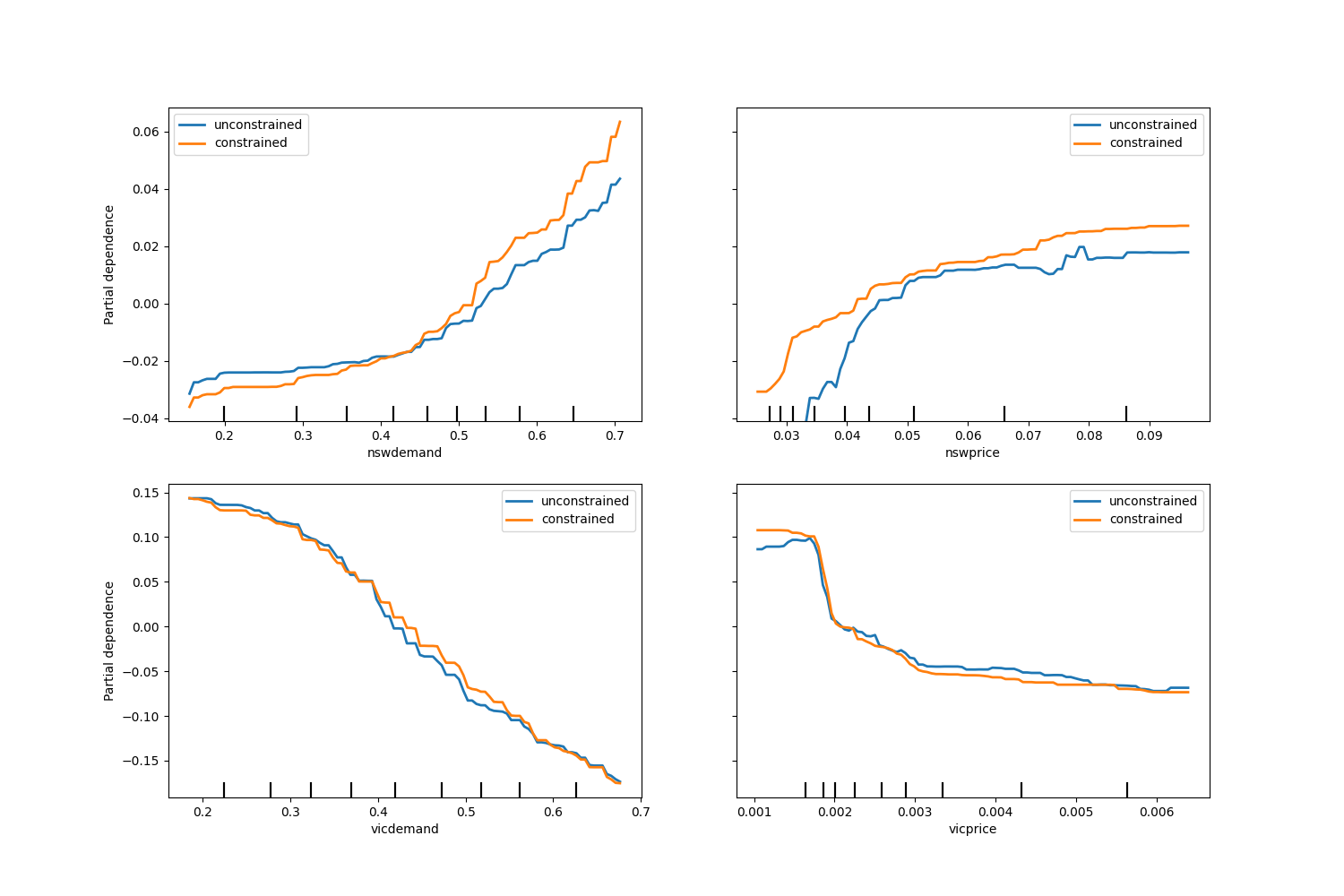
plot hgbt regression

请注意， nswdemand 和 vicdemand 似乎在没有约束的情况下已经是单调的。 这是一个很好的例子，表明带有单调性约束的模型是“过度约束”的。

此外，我们可以验证通过引入单调约束，模型的预测质量不会显著下降。为此，我们使用 TimeSeriesSplit 交叉验证来估计测试分数的方差。这样做可以保证训练数据不会超过测试数据，这在处理具有时间关系的数据时至关重要。

from sklearn.metrics import make_scorer, root_mean_squared_error
from sklearn.model_selection import TimeSeriesSplit, cross_validate

ts_cv = TimeSeriesSplit(n_splits=5, gap=48, test_size=336)  # a week has 336 samples
scorer = make_scorer(root_mean_squared_error)

cv_results = cross_validate(hgbt_no_cst, X, y, cv=ts_cv, scoring=scorer)
rmse = cv_results["test_score"]
print(f"RMSE without constraints = {rmse.mean():.3f} +/- {rmse.std():.3f}")

cv_results = cross_validate(hgbt_cst, X, y, cv=ts_cv, scoring=scorer)
rmse = cv_results["test_score"]
print(f"RMSE with constraints    = {rmse.mean():.3f} +/- {rmse.std():.3f}")

RMSE without constraints = 0.103 +/- 0.030
RMSE with constraints    = 0.107 +/- 0.034

话虽如此，请注意，比较的是两个不同的模型，它们可能通过不同的超参数组合进行优化。这就是为什么我们在本节中不使用之前使用的 common_params 。

Total running time of the script: (0 minutes 18.835 seconds)

Related examples

比较随机森林和直方图梯度提升模型

比较随机森林和直方图梯度提升模型

时间序列预测的滞后特征

时间序列预测的滞后特征

单调约束

单调约束

目标编码器与其他编码器的比较

目标编码器与其他编码器的比较

Gallery generated by Sphinx-Gallery

On this page
Show Source