Note

Go to the end to download the full example code. or to run this example in your browser via Binder

接收者操作特性（ROC）与交叉验证#

本示例展示了如何使用交叉验证来估计和可视化接收者操作特性（ROC）指标的方差。

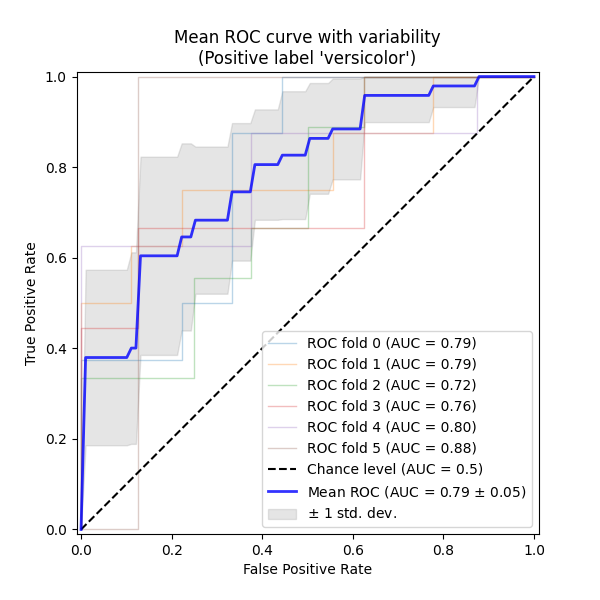
ROC 曲线通常在 Y 轴上显示真正率（TPR），在 X 轴上显示假正率（FPR）。这意味着图的左上角是“理想”点——FPR 为零，TPR 为一。这虽然不太现实，但通常来说，曲线下面积（AUC）越大越好。ROC 曲线的“陡峭度”也很重要，因为理想情况下应最大化 TPR，同时最小化 FPR。

本示例展示了通过 K 折交叉验证创建的不同数据集的 ROC 响应。通过这些曲线，可以计算平均 AUC，并观察当训练集被分成不同子集时曲线的方差。这大致显示了分类器输出如何受训练数据变化的影响，以及 K 折交叉验证生成的不同分割之间的差异。

Note

请参阅多分类接收者操作特性（ROC），该示例补充了当前示例，解释了将指标推广到多类分类器的平均策略。

加载和准备数据#

我们导入了 Iris plants dataset ，其中包含3个类别，每个类别对应一种鸢尾花类型。一个类别与其他两个类别是线性可分的；而后两者之间不是线性可分的。

在接下来的步骤中，我们通过去除“virginica”类（ class_id=2 ）来将数据集二值化。这意味着“versicolor”类（ class_id=1 ）被视为正类，而“setosa”类（ class_id=0 ）被视为负类。

import numpy as np

from sklearn.datasets import load_iris

iris = load_iris()
target_names = iris.target_names
X, y = iris.data, iris.target
X, y = X[y != 2], y[y != 2]
n_samples, n_features = X.shape

我们还添加了噪声特征以增加问题的难度。

random_state = np.random.RandomState(0)
X = np.concatenate([X, random_state.randn(n_samples, 200 * n_features)], axis=1)

分类和ROC分析#

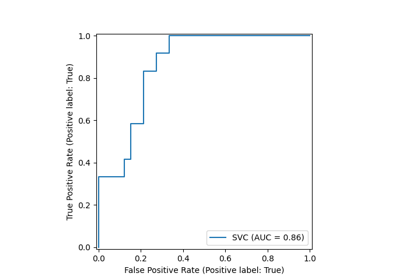
我们在这里运行一个 SVC 分类器，并使用交叉验证绘制每折的 ROC 曲线。请注意，用于定义机会水平（虚线 ROC 曲线）的基线是一个总是预测最频繁类别的分类器。

import matplotlib.pyplot as plt

from sklearn import svm
from sklearn.metrics import RocCurveDisplay, auc
from sklearn.model_selection import StratifiedKFold

n_splits = 6
cv = StratifiedKFold(n_splits=n_splits)
classifier = svm.SVC(kernel="linear", probability=True, random_state=random_state)

tprs = []
aucs = []
mean_fpr = np.linspace(0, 1, 100)

fig, ax = plt.subplots(figsize=(6, 6))
for fold, (train, test) in enumerate(cv.split(X, y)):
    classifier.fit(X[train], y[train])
    viz = RocCurveDisplay.from_estimator(
        classifier,
        X[test],
        y[test],
        name=f"ROC fold {fold}",
        alpha=0.3,
        lw=1,
        ax=ax,
        plot_chance_level=(fold == n_splits - 1),
    )
    interp_tpr = np.interp(mean_fpr, viz.fpr, viz.tpr)
    interp_tpr[0] = 0.0
    tprs.append(interp_tpr)
    aucs.append(viz.roc_auc)

mean_tpr = np.mean(tprs, axis=0)
mean_tpr[-1] = 1.0
mean_auc = auc(mean_fpr, mean_tpr)
std_auc = np.std(aucs)
ax.plot(
    mean_fpr,
    mean_tpr,
    color="b",
    label=r"Mean ROC (AUC = %0.2f $\pm$ %0.2f)" % (mean_auc, std_auc),
    lw=2,
    alpha=0.8,
)

std_tpr = np.std(tprs, axis=0)
tprs_upper = np.minimum(mean_tpr + std_tpr, 1)
tprs_lower = np.maximum(mean_tpr - std_tpr, 0)
ax.fill_between(
    mean_fpr,
    tprs_lower,
    tprs_upper,
    color="grey",
    alpha=0.2,
    label=r"$\pm$ 1 std. dev.",
)

ax.set(
    xlabel="False Positive Rate",
    ylabel="True Positive Rate",
    title=f"Mean ROC curve with variability\n(Positive label '{target_names[1]}')",
)
ax.legend(loc="lower right")
plt.show()