Note

Go to the end to download the full example code. or to run this example in your browser via Binder

线性回归示例#

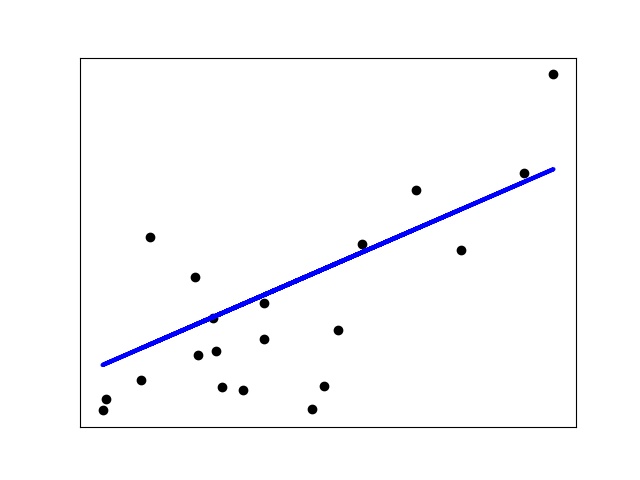
下面的示例仅使用 diabetes 数据集的第一个特征，以便在二维图中展示数据点。在图中可以看到一条直线，显示了线性回归如何尝试绘制一条直线，以最佳地最小化数据集中观察到的响应与线性近似预测的响应之间的残差平方和。

还计算了系数、残差平方和以及决定系数。

Coefficients:
 [938.23786125]
Mean squared error: 2548.07
Coefficient of determination: 0.47

# 代码来源：Jaques Grobler
# SPDX许可证标识符：BSD-3-Clause

import matplotlib.pyplot as plt
import numpy as np

from sklearn import datasets, linear_model
from sklearn.metrics import mean_squared_error, r2_score

# 加载糖尿病数据集
diabetes_X, diabetes_y = datasets.load_diabetes(return_X_y=True)

# 只使用一个特征
diabetes_X = diabetes_X[:, np.newaxis, 2]

# 将数据分成训练集和测试集
diabetes_X_train = diabetes_X[:-20]
diabetes_X_test = diabetes_X[-20:]

# 将目标分成训练集和测试集
diabetes_y_train = diabetes_y[:-20]
diabetes_y_test = diabetes_y[-20:]

# 创建线性回归对象
regr = linear_model.LinearRegression()

# 使用训练集训练模型
regr.fit(diabetes_X_train, diabetes_y_train)

# 使用测试集进行预测
diabetes_y_pred = regr.predict(diabetes_X_test)

# The coefficients
print("Coefficients: \n", regr.coef_)
# 均方误差
print("Mean squared error: %.2f" % mean_squared_error(diabetes_y_test, diabetes_y_pred))
# 决定系数：1 是完美预测
print("Coefficient of determination: %.2f" % r2_score(diabetes_y_test, diabetes_y_pred))

# 绘图输出
plt.scatter(diabetes_X_test, diabetes_y_test, color="black")
plt.plot(diabetes_X_test, diabetes_y_pred, color="blue", linewidth=3)

plt.xticks(())
plt.yticks(())

plt.show()