Note

Go to the end to download the full example code. or to run this example in your browser via Binder

多标签分类#

这个示例模拟了一个多标签文档分类问题。数据集是基于以下过程随机生成的：

选择标签数量：n ~ 泊松分布(n_labels)

选择n次类别c：c ~ 多项分布(theta)

选择文档长度：k ~ 泊松分布(length)

选择k次单词：w ~ 多项分布(theta_c)

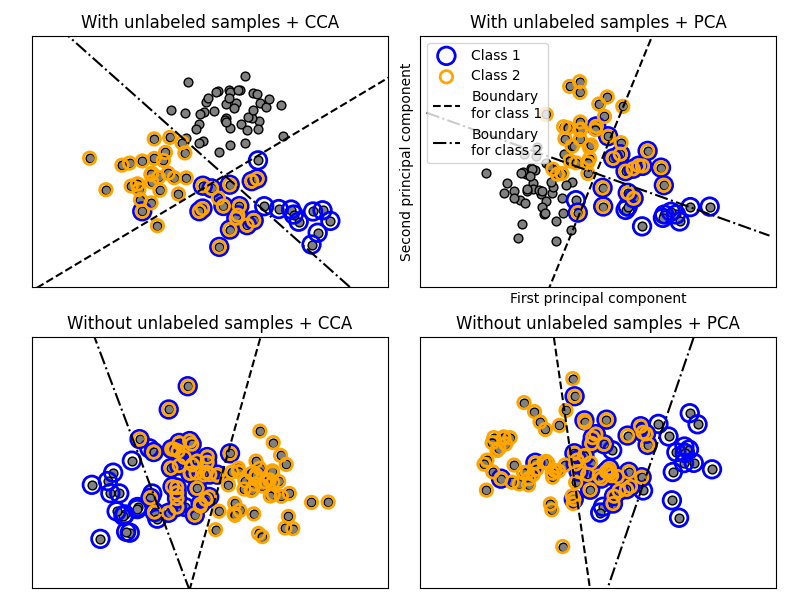
在上述过程中，使用拒绝采样确保n大于2，并且文档长度不为零。同样，我们拒绝已经选择的类别。分配给两个类别的文档被绘制在两个彩色圆圈中。

分类通过投影到PCA和CCA找到的前两个主成分进行，以便于可视化，然后使用:class:~sklearn.multiclass.OneVsRestClassifier 元分类器，使用两个具有线性核的SVC来学习每个类别的判别模型。请注意，PCA用于执行无监督的降维，而CCA用于执行有监督的降维。

注意：在图中，“未标记样本”并不意味着我们不知道标签（如在半监督学习中），而是样本根本没有标签。

With unlabeled samples + CCA, With unlabeled samples + PCA, Without unlabeled samples + CCA, Without unlabeled samples + PCA

# 作者：scikit-learn 开发者
# SPDX 许可证标识符：BSD-3-Clause

import matplotlib.pyplot as plt
import numpy as np

from sklearn.cross_decomposition import CCA
from sklearn.datasets import make_multilabel_classification
from sklearn.decomposition import PCA
from sklearn.multiclass import OneVsRestClassifier
from sklearn.svm import SVC


def plot_hyperplane(clf, min_x, max_x, linestyle, label):
    # 获得分离超平面
    w = clf.coef_[0]
    a = -w[0] / w[1]
    xx = np.linspace(min_x - 5, max_x + 5)  # make sure the line is long enough
    yy = a * xx - (clf.intercept_[0]) / w[1]
    plt.plot(xx, yy, linestyle, label=label)


def plot_subfigure(X, Y, subplot, title, transform):
    if transform == "pca":
        X = PCA(n_components=2).fit_transform(X)
    elif transform == "cca":
        X = CCA(n_components=2).fit(X, Y).transform(X)
    else:
        raise ValueError

    min_x = np.min(X[:, 0])
    max_x = np.max(X[:, 0])

    min_y = np.min(X[:, 1])
    max_y = np.max(X[:, 1])

    classif = OneVsRestClassifier(SVC(kernel="linear"))
    classif.fit(X, Y)

    plt.subplot(2, 2, subplot)
    plt.title(title)

    zero_class = np.where(Y[:, 0])
    one_class = np.where(Y[:, 1])
    plt.scatter(X[:, 0], X[:, 1], s=40, c="gray", edgecolors=(0, 0, 0))
    plt.scatter(
        X[zero_class, 0],
        X[zero_class, 1],
        s=160,
        edgecolors="b",
        facecolors="none",
        linewidths=2,
        label="Class 1",
    )
    plt.scatter(
        X[one_class, 0],
        X[one_class, 1],
        s=80,
        edgecolors="orange",
        facecolors="none",
        linewidths=2,
        label="Class 2",
    )

    plot_hyperplane(
        classif.estimators_[0], min_x, max_x, "k--", "Boundary\nfor class 1"
    )
    plot_hyperplane(
        classif.estimators_[1], min_x, max_x, "k-.", "Boundary\nfor class 2"
    )
    plt.xticks(())
    plt.yticks(())

    plt.xlim(min_x - 0.5 * max_x, max_x + 0.5 * max_x)
    plt.ylim(min_y - 0.5 * max_y, max_y + 0.5 * max_y)
    if subplot == 2:
        plt.xlabel("First principal component")
        plt.ylabel("Second principal component")
        plt.legend(loc="upper left")


plt.figure(figsize=(8, 6))

X, Y = make_multilabel_classification(
    n_classes=2, n_labels=1, allow_unlabeled=True, random_state=1
)

plot_subfigure(X, Y, 1, "With unlabeled samples + CCA", "cca")
plot_subfigure(X, Y, 2, "With unlabeled samples + PCA", "pca")

X, Y = make_multilabel_classification(
    n_classes=2, n_labels=1, allow_unlabeled=False, random_state=1
)

plot_subfigure(X, Y, 3, "Without unlabeled samples + CCA", "cca")
plot_subfigure(X, Y, 4, "Without unlabeled samples + PCA", "pca")

plt.subplots_adjust(0.04, 0.02, 0.97, 0.94, 0.09, 0.2)
plt.show()