Note

Go to the end to download the full example code. or to run this example in your browser via Binder

比较用于异常检测的算法在玩具数据集上的表现#

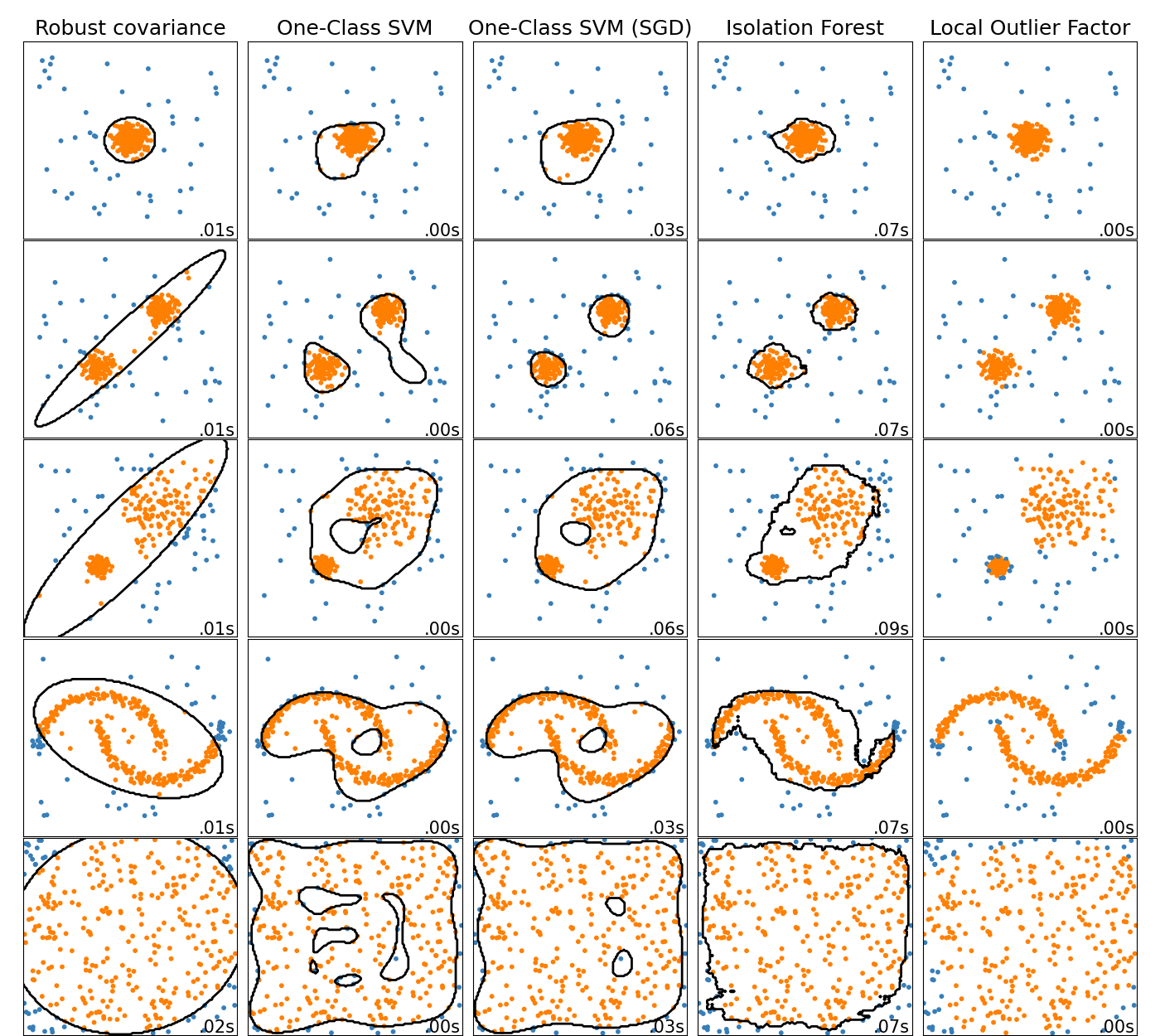
本示例展示了不同异常检测算法在二维数据集上的特性。数据集包含一个或两个模式（高密度区域），以说明算法处理多模态数据的能力。

对于每个数据集，15%的样本是随机生成的均匀噪声。这个比例是赋予OneClassSVM的nu参数和其他异常检测算法的污染参数的值。内点和外点之间的决策边界以黑色显示，除了局部异常因子（LOF），因为它在用于异常检测时没有可应用于新数据的预测方法。

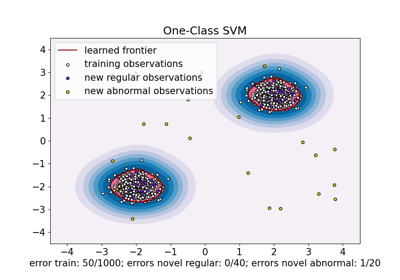
OneClassSVM 已知对异常值敏感，因此在异常检测方面表现不佳。该估计器最适合用于训练集不被异常值污染的新颖性检测。也就是说，在高维度或对内点数据分布没有任何假设的情况下进行异常检测是非常具有挑战性的，单类SVM在这些情况下可能会根据其超参数的值给出有用的结果。

sklearn.linear_model.SGDOneClassSVM 是基于随机梯度下降（SGD）的单类SVM的实现。结合核近似，该估计器可用于近似核化的:class:sklearn.svm.OneClassSVM 的解。我们注意到，尽管不完全相同，sklearn.linear_model.SGDOneClassSVM 和:class:sklearn.svm.OneClassSVM 的决策边界非常相似。使用:class:sklearn.linear_model.SGDOneClassSVM 的主要优势在于它随样本数量线性扩展。

sklearn.covariance.EllipticEnvelope 假设数据是高斯分布并学习一个椭圆。因此，当数据不是单峰时，它的表现会变差。然而请注意，该估计器对异常值具有鲁棒性。

IsolationForest 和:class:~sklearn.neighbors.LocalOutlierFactor 似乎在多模态数据集上表现相当不错。LocalOutlierFactor 相对于其他估计器的优势在于第三个数据集，其中两个模式具有不同的密度。这一优势可以通过LOF的局部特性来解释，这意味着它只将一个样本的异常分数与其邻居的分数进行比较。

最后，对于最后一个数据集，很难说一个样本比另一个样本更异常，因为它们在超立方体中均匀分布。除了有点过拟合的:class:~sklearn.svm.OneClassSVM ，所有估计器在这种情况下都表现出不错的解决方案。在这种情况下，明智的做法是更仔细地查看样本的异常分数，因为一个好的估计器应该为所有样本分配相似的分数。

虽然这些示例提供了一些关于算法的直觉，但这种直觉可能不适用于非常高维的数据。

最后，请注意，这些模型的参数在这里是手工挑选的，但在实际中需要进行调整。在没有标记数据的情况下，问题是完全无监督的，因此模型选择可能是一个挑战。

Robust covariance, One-Class SVM, One-Class SVM (SGD), Isolation Forest, Local Outlier Factor

# 作者：scikit-learn 开发者
# SPDX 许可证标识符：BSD-3-Clause

import time

import matplotlib
import matplotlib.pyplot as plt
import numpy as np

from sklearn import svm
from sklearn.covariance import EllipticEnvelope
from sklearn.datasets import make_blobs, make_moons
from sklearn.ensemble import IsolationForest
from sklearn.kernel_approximation import Nystroem
from sklearn.linear_model import SGDOneClassSVM
from sklearn.neighbors import LocalOutlierFactor
from sklearn.pipeline import make_pipeline

matplotlib.rcParams["contour.negative_linestyle"] = "solid"

# 示例设置
n_samples = 300
outliers_fraction = 0.15
n_outliers = int(outliers_fraction * n_samples)
n_inliers = n_samples - n_outliers

# 定义要比较的异常值/异常检测方法。
# SGDOneClassSVM必须与核近似一起在管道中使用，以提供与OneClassSVM相似的结果。
anomaly_algorithms = [
    (
        "Robust covariance",
        EllipticEnvelope(contamination=outliers_fraction, random_state=42),
    ),
    ("One-Class SVM", svm.OneClassSVM(nu=outliers_fraction, kernel="rbf", gamma=0.1)),
    (
        "One-Class SVM (SGD)",
        make_pipeline(
            Nystroem(gamma=0.1, random_state=42, n_components=150),
            SGDOneClassSVM(
                nu=outliers_fraction,
                shuffle=True,
                fit_intercept=True,
                random_state=42,
                tol=1e-6,
            ),
        ),
    ),
    (
        "Isolation Forest",
        IsolationForest(contamination=outliers_fraction, random_state=42),
    ),
    (
        "Local Outlier Factor",
        LocalOutlierFactor(n_neighbors=35, contamination=outliers_fraction),
    ),
]

# 定义数据集
blobs_params = dict(random_state=0, n_samples=n_inliers, n_features=2)
datasets = [
    make_blobs(centers=[[0, 0], [0, 0]], cluster_std=0.5, **blobs_params)[0],
    make_blobs(centers=[[2, 2], [-2, -2]], cluster_std=[0.5, 0.5], **blobs_params)[0],
    make_blobs(centers=[[2, 2], [-2, -2]], cluster_std=[1.5, 0.3], **blobs_params)[0],
    4.0
    * (
        make_moons(n_samples=n_samples, noise=0.05, random_state=0)[0]
        - np.array([0.5, 0.25])
    ),
    14.0 * (np.random.RandomState(42).rand(n_samples, 2) - 0.5),
]

# 在给定设置下比较给定的分类器
xx, yy = np.meshgrid(np.linspace(-7, 7, 150), np.linspace(-7, 7, 150))

plt.figure(figsize=(len(anomaly_algorithms) * 2 + 4, 12.5))
plt.subplots_adjust(
    left=0.02, right=0.98, bottom=0.001, top=0.96, wspace=0.05, hspace=0.01
)

plot_num = 1
rng = np.random.RandomState(42)

for i_dataset, X in enumerate(datasets):
    # 添加异常值
    X = np.concatenate([X, rng.uniform(low=-6, high=6, size=(n_outliers, 2))], axis=0)

    for name, algorithm in anomaly_algorithms:
        t0 = time.time()
        algorithm.fit(X)
        t1 = time.time()
        plt.subplot(len(datasets), len(anomaly_algorithms), plot_num)
        if i_dataset == 0:
            plt.title(name, size=18)

        # 拟合数据并标记异常值
        if name == "Local Outlier Factor":
            y_pred = algorithm.fit_predict(X)
        else:
            y_pred = algorithm.fit(X).predict(X)

        # 绘制等高线和点
        if name != "Local Outlier Factor":  # LOF does not implement predict
            Z = algorithm.predict(np.c_[xx.ravel(), yy.ravel()])
            Z = Z.reshape(xx.shape)
            plt.contour(xx, yy, Z, levels=[0], linewidths=2, colors="black")

        colors = np.array(["#377eb8", "#ff7f00"])
        plt.scatter(X[:, 0], X[:, 1], s=10, color=colors[(y_pred + 1) // 2])

        plt.xlim(-7, 7)
        plt.ylim(-7, 7)
        plt.xticks(())
        plt.yticks(())
        plt.text(
            0.99,
            0.01,
            ("%.2fs" % (t1 - t0)).lstrip("0"),
            transform=plt.gca().transAxes,
            size=15,
            horizontalalignment="right",
        )
        plot_num += 1

plt.show()