矢量量化示例

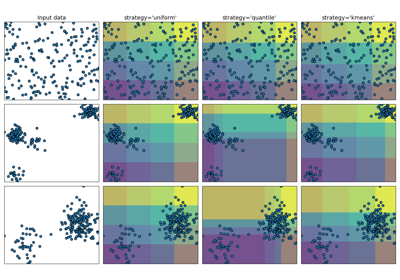
此示例展示了如何使用 KBinsDiscretizer 对一组玩具图像（浣熊脸）进行矢量量化。

# 作者：scikit-learn 开发者
# SPDX 许可证标识符：BSD-3-Clause

原始图像

我们首先从 SciPy 加载浣熊脸图像。我们还将检查一些关于图像的信息，例如图像的形状和用于存储图像的数据类型。

请注意，根据SciPy版本的不同，我们需要调整导入方式，因为返回图像的函数所在的模块不同。此外，SciPy >= 1.10 需要安装 pooch 包。

try:  # Scipy >= 1.10
    from scipy.datasets import face
except ImportError:
    from scipy.misc import face

raccoon_face = face(gray=True)

print(f"The dimension of the image is {raccoon_face.shape}")
print(f"The data used to encode the image is of type {raccoon_face.dtype}")
print(f"The number of bytes taken in RAM is {raccoon_face.nbytes}")

The dimension of the image is (768, 1024)
The data used to encode the image is of type uint8
The number of bytes taken in RAM is 786432

因此，该图像是一个高度为768像素、宽度为1024像素的二维数组。每个值是一个8位无符号整数，这意味着图像使用每像素8位进行编码。图像的总内存使用量为786千字节（1字节等于8位）。

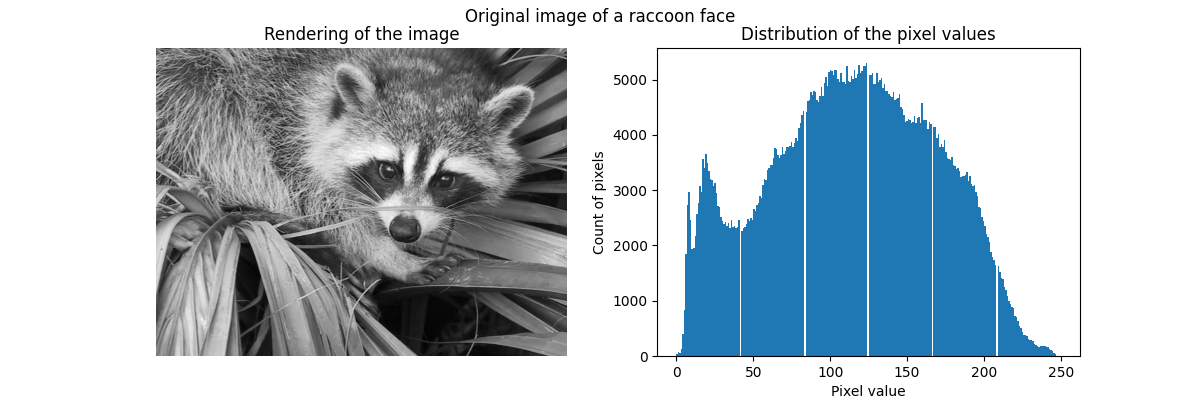
使用8位无符号整数意味着图像最多使用256种不同的灰度级进行编码。我们可以检查这些值的分布。

import matplotlib.pyplot as plt

fig, ax = plt.subplots(ncols=2, figsize=(12, 4))

ax[0].imshow(raccoon_face, cmap=plt.cm.gray)
ax[0].axis("off")
ax[0].set_title("Rendering of the image")
ax[1].hist(raccoon_face.ravel(), bins=256)
ax[1].set_xlabel("Pixel value")
ax[1].set_ylabel("Count of pixels")
ax[1].set_title("Distribution of the pixel values")
_ = fig.suptitle("Original image of a raccoon face")

通过矢量量化进行压缩

通过矢量量化进行压缩的思想是减少表示图像的灰度级数量。例如，我们可以使用8个值代替256个值。因此，这意味着我们可以有效地使用3位而不是8位来编码单个像素，从而将内存使用量减少大约2.5倍。我们稍后将讨论这种内存使用情况。

编码策略

可以使用 KBinsDiscretizer 进行压缩。我们需要选择一种策略来定义 8 个灰度值进行子采样。最简单的策略是将它们等距定义，这对应于设置 strategy="uniform" 。从之前的直方图中，我们知道这种策略肯定不是最优的。

from sklearn.preprocessing import KBinsDiscretizer

n_bins = 8
encoder = KBinsDiscretizer(
    n_bins=n_bins,
    encode="ordinal",
    strategy="uniform",
    random_state=0,
)
compressed_raccoon_uniform = encoder.fit_transform(raccoon_face.reshape(-1, 1)).reshape(
    raccoon_face.shape
)

fig, ax = plt.subplots(ncols=2, figsize=(12, 4))
ax[0].imshow(compressed_raccoon_uniform, cmap=plt.cm.gray)
ax[0].axis("off")
ax[0].set_title("Rendering of the image")
ax[1].hist(compressed_raccoon_uniform.ravel(), bins=256)
ax[1].set_xlabel("Pixel value")
ax[1].set_ylabel("Count of pixels")
ax[1].set_title("Sub-sampled distribution of the pixel values")
_ = fig.suptitle("Raccoon face compressed using 3 bits and a uniform strategy")

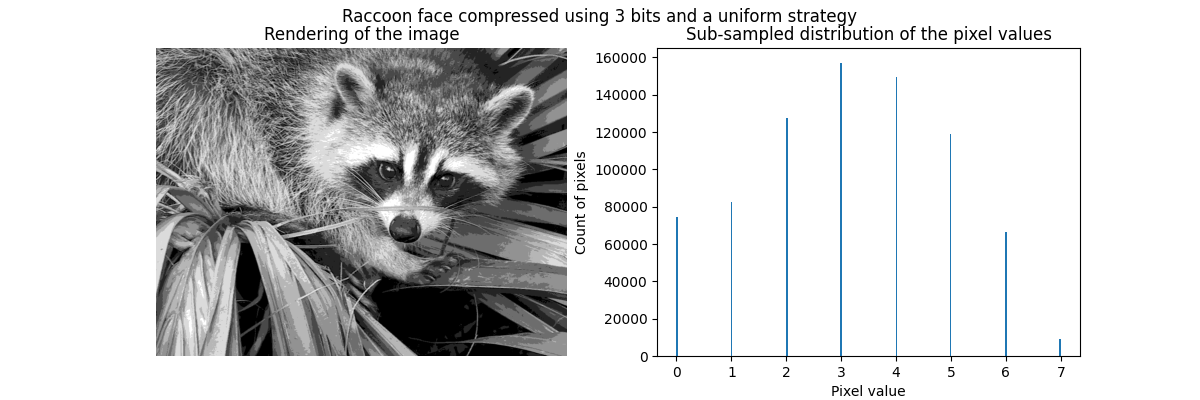
从定性上看，我们可以发现一些小区域在压缩后有影响（例如右下角的叶子）。但总的来说，生成的图像仍然看起来不错。

我们观察到像素值的分布已被映射到8个不同的值。我们可以检查这些值与原始像素值之间的对应关系。

bin_edges = encoder.bin_edges_[0]
bin_center = bin_edges[:-1] + (bin_edges[1:] - bin_edges[:-1]) / 2
bin_center

array([ 15.625,  46.875,  78.125, 109.375, 140.625, 171.875, 203.125,
       234.375])

_, ax = plt.subplots()
ax.hist(raccoon_face.ravel(), bins=256)
color = "tab:orange"
for center in bin_center:
    ax.axvline(center, color=color)
    ax.text(center - 10, ax.get_ybound()[1] + 100, f"{center:.1f}", color=color)

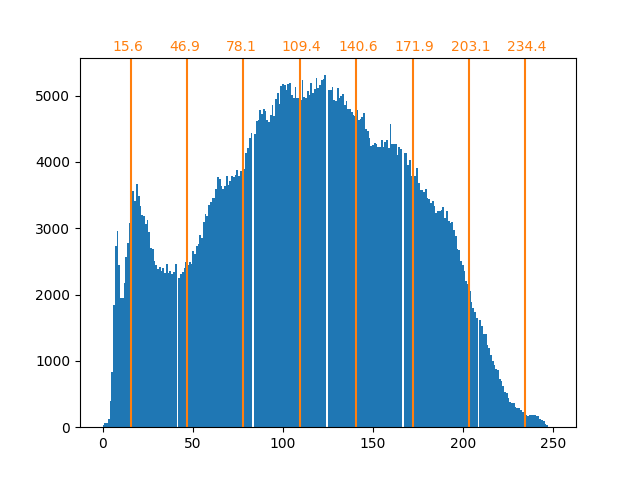
正如前面所述，均匀采样策略并不是最优的。请注意，例如映射到值7的像素将编码相当少量的信息，而映射到值3的像素将表示大量的计数。我们可以改用诸如k-means之类的聚类策略来找到更优的映射。

encoder = KBinsDiscretizer(
    n_bins=n_bins,
    encode="ordinal",
    strategy="kmeans",
    random_state=0,
)
compressed_raccoon_kmeans = encoder.fit_transform(raccoon_face.reshape(-1, 1)).reshape(
    raccoon_face.shape
)

fig, ax = plt.subplots(ncols=2, figsize=(12, 4))
ax[0].imshow(compressed_raccoon_kmeans, cmap=plt.cm.gray)
ax[0].axis("off")
ax[0].set_title("Rendering of the image")
ax[1].hist(compressed_raccoon_kmeans.ravel(), bins=256)
ax[1].set_xlabel("Pixel value")
ax[1].set_ylabel("Number of pixels")
ax[1].set_title("Distribution of the pixel values")
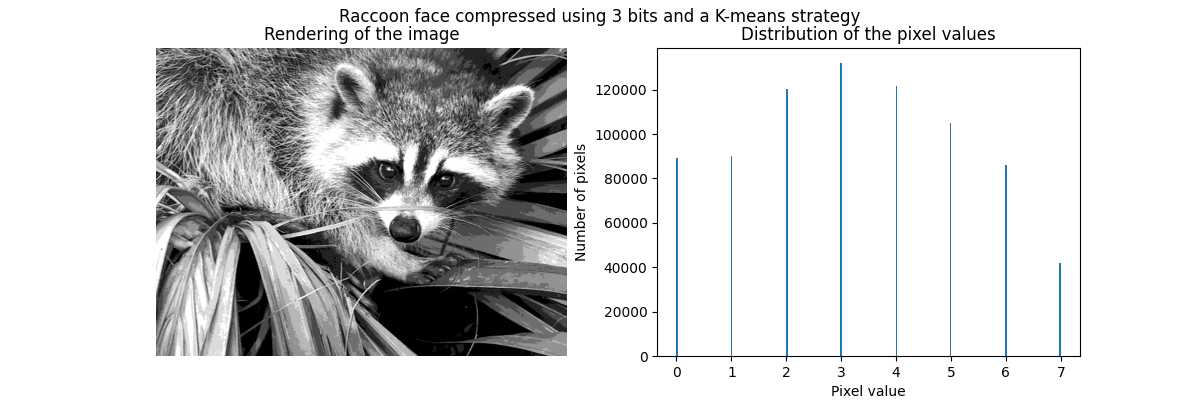
_ = fig.suptitle("Raccoon face compressed using 3 bits and a K-means strategy")

bin_edges = encoder.bin_edges_[0]
bin_center = bin_edges[:-1] + (bin_edges[1:] - bin_edges[:-1]) / 2
bin_center

array([ 18.90885631,  53.34346583,  82.64447187, 109.28225276,
       134.70763101, 159.78681467, 185.17226834, 224.02069427])

_, ax = plt.subplots()
ax.hist(raccoon_face.ravel(), bins=256)
color = "tab:orange"
for center in bin_center:
    ax.axvline(center, color=color)
    ax.text(center - 10, ax.get_ybound()[1] + 100, f"{center:.1f}", color=color)

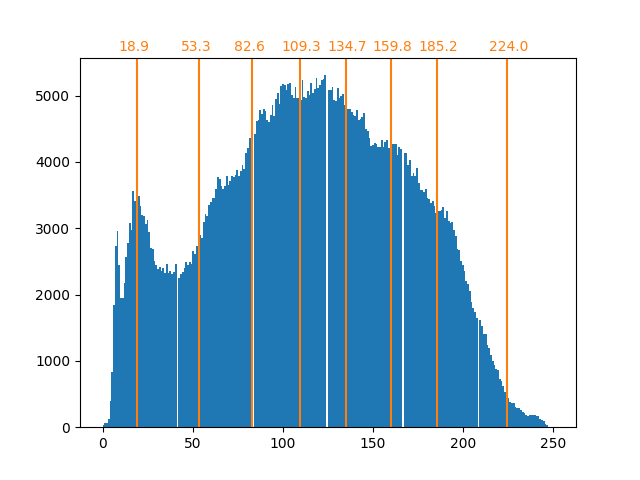
现在，各个箱中的计数更加均衡，并且它们的中心不再是等距的。请注意，我们可以通过使用 strategy="quantile" 而不是 strategy="kmeans" 来强制每个箱中的像素数量相同。

内存占用

我们之前说过，我们应该节省8倍的内存。让我们来验证一下。

print(f"The number of bytes taken in RAM is {compressed_raccoon_kmeans.nbytes}")
print(f"Compression ratio: {compressed_raccoon_kmeans.nbytes / raccoon_face.nbytes}")

The number of bytes taken in RAM is 6291456
Compression ratio: 8.0

令人惊讶的是，我们的压缩图像占用了比原始图像多8倍的内存。这确实与我们的预期相反。其主要原因在于用于编码图像的数据类型。

print(f"Type of the compressed image: {compressed_raccoon_kmeans.dtype}")

Type of the compressed image: float64

确实，KBinsDiscretizer 的输出是一个64位浮点数组。这意味着它占用了8倍的内存。然而，我们使用这种64位浮点表示来编码8个值。实际上，只有当我们将压缩图像转换为3位整数数组时，才能节省内存。我们可以使用 numpy.ndarray.astype 方法。然而，3位整数表示并不存在，并且为了编码这8个值，我们也需要使用8位无符号整数表示。

实际上，观察到内存增益需要原始图像是64位浮点表示。

Related examples

使用字典学习进行图像去噪

使用字典学习进行图像去噪

使用K均值的颜色量化

使用K均值的颜色量化

展示KBinsDiscretizer的不同策略

展示KBinsDiscretizer的不同策略

识别手写数字

识别手写数字