Note
Go to the end to download the full example code. or to run this example in your browser via Binder
后处理调整决策函数的截断点#
一旦训练了一个二元分类器,predict 方法会输出与 decision_function 或 predict_proba 输出的阈值对应的类别标签预测。默认阈值定义为0.5的后验概率估计或0.0的决策分数。然而,这种默认策略可能并不是针对当前任务的最佳选择。
本示例展示了如何使用 TunedThresholdClassifierCV 根据感兴趣的指标来调整决策阈值。
糖尿病数据集#
为了说明决策阈值的调整,我们将使用糖尿病数据集。该数据集可在 OpenML 上获取:https://www.openml.org/d/37。我们使用 fetch_openml 函数来获取该数据集。
from sklearn.datasets import fetch_openml
diabetes = fetch_openml(data_id=37, as_frame=True, parser="pandas")
data, target = diabetes.data, diabetes.target
我们查看目标以了解我们正在处理的问题类型。
target.value_counts()
class
tested_negative 500
tested_positive 268
Name: count, dtype: int64
我们可以看到我们正在处理一个二元分类问题。由于标签没有编码为0和1,我们明确表示将标记为“tested_negative”的类视为负类(这也是最常见的),而将标记为“tested_positive”的类视为正类。
neg_label, pos_label = target.value_counts().index
我们还可以观察到这个二元问题有些不平衡,其中负类样本的数量大约是正类样本的两倍。在评估时,我们应考虑这一点来解释结果。
我们的基础分类器#
我们定义了一个基本的预测模型,该模型由一个缩放器和一个逻辑回归分类器组成。
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
model = make_pipeline(StandardScaler(), LogisticRegression())
model
我们使用交叉验证来评估我们的模型。我们使用准确率和平衡准确率来报告我们模型的性能。平衡准确率是一种对类别不平衡不太敏感的指标,它将使我们能够更全面地看待准确率得分。
交叉验证使我们能够研究不同数据分割中决策阈值的方差。然而,数据集相当小,使用超过5折来评估离散度会有害。因此,我们使用 RepeatedStratifiedKFold ,在其中应用多次5折交叉验证。
import pandas as pd
from sklearn.model_selection import RepeatedStratifiedKFold, cross_validate
scoring = ["accuracy", "balanced_accuracy"]
cv_scores = [
"train_accuracy",
"test_accuracy",
"train_balanced_accuracy",
"test_balanced_accuracy",
]
cv = RepeatedStratifiedKFold(n_splits=5, n_repeats=10, random_state=42)
cv_results_vanilla_model = pd.DataFrame(
cross_validate(
model,
data,
target,
scoring=scoring,
cv=cv,
return_train_score=True,
return_estimator=True,
)
)
cv_results_vanilla_model[cv_scores].aggregate(["mean", "std"]).T
我们的预测模型成功地掌握了数据与目标之间的关系。训练和测试得分接近,意味着我们的预测模型没有过拟合。我们还可以观察到,平衡准确率低于准确率,这是由于之前提到的类别不平衡所致。
对于这个分类器,我们将用于将正类概率转换为类别预测的决策阈值设为默认值:0.5。然而,这个阈值可能不是最优的。如果我们的目标是最大化平衡准确率,我们应该选择另一个能够最大化该指标的阈值。
TunedThresholdClassifierCV 元估计器允许根据感兴趣的指标调整分类器的决策阈值。
调整决策阈值#
我们创建一个 TunedThresholdClassifierCV 并将其配置为最大化平衡准确率。我们使用与之前相同的交叉验证策略来评估模型。
from sklearn.model_selection import TunedThresholdClassifierCV
tuned_model = TunedThresholdClassifierCV(estimator=model, scoring="balanced_accuracy")
cv_results_tuned_model = pd.DataFrame(
cross_validate(
tuned_model,
data,
target,
scoring=scoring,
cv=cv,
return_train_score=True,
return_estimator=True,
)
)
cv_results_tuned_model[cv_scores].aggregate(["mean", "std"]).T
与原始模型相比,我们观察到平衡准确率得分有所提高。当然,这是以较低的准确率得分为代价的。这意味着我们的模型现在对正类更加敏感,但在负类上犯了更多错误。
然而,重要的是要注意,这个经过调优的预测模型在内部与原始模型是相同的:它们具有相同的拟合系数。
import matplotlib.pyplot as plt
vanilla_model_coef = pd.DataFrame(
[est[-1].coef_.ravel() for est in cv_results_vanilla_model["estimator"]],
columns=diabetes.feature_names,
)
tuned_model_coef = pd.DataFrame(
[est.estimator_[-1].coef_.ravel() for est in cv_results_tuned_model["estimator"]],
columns=diabetes.feature_names,
)
fig, ax = plt.subplots(ncols=2, figsize=(12, 4), sharex=True, sharey=True)
vanilla_model_coef.boxplot(ax=ax[0])
ax[0].set_ylabel("Coefficient value")
ax[0].set_title("Vanilla model")
tuned_model_coef.boxplot(ax=ax[1])
ax[1].set_title("Tuned model")
_ = fig.suptitle("Coefficients of the predictive models")
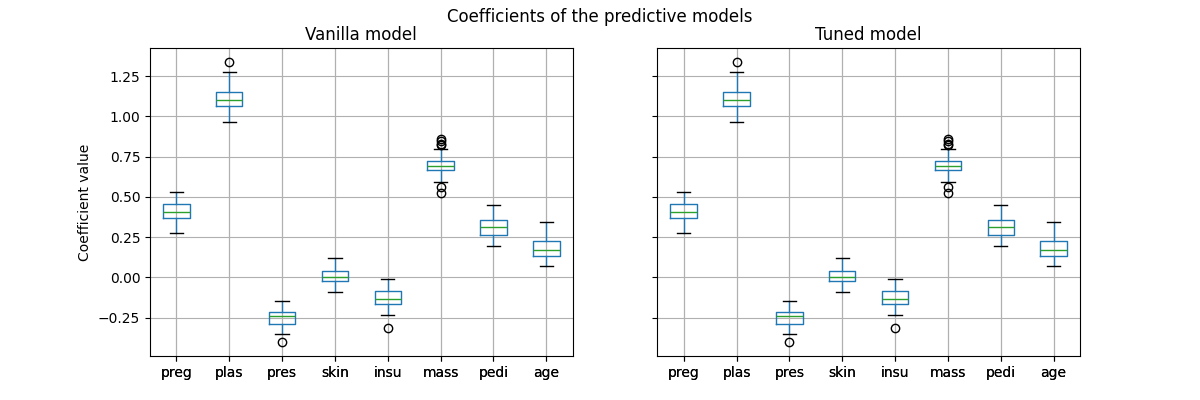
仅在交叉验证期间更改了每个模型的决策阈值。
decision_threshold = pd.Series(
[est.best_threshold_ for est in cv_results_tuned_model["estimator"]],
)
ax = decision_threshold.plot.kde()
ax.axvline(
decision_threshold.mean(),
color="k",
linestyle="--",
label=f"Mean decision threshold: {decision_threshold.mean():.2f}",
)
ax.set_xlabel("Decision threshold")
ax.legend(loc="upper right")
_ = ax.set_title(
"Distribution of the decision threshold \nacross different cross-validation folds"
)
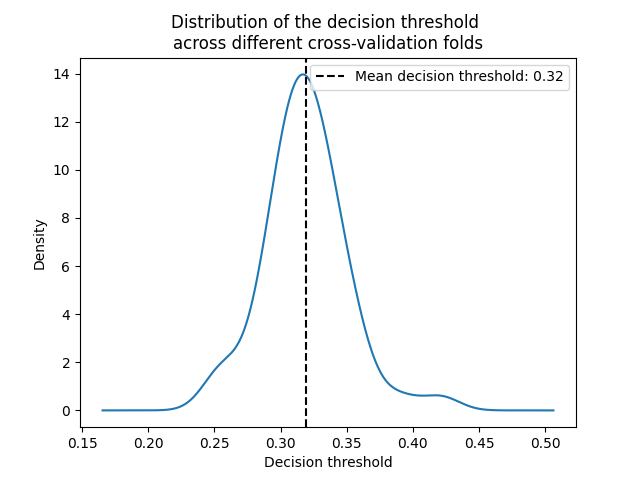
通常情况下,决策阈值在0.32左右时可以最大化平衡准确率,这与默认的0.5决策阈值不同。因此,当预测模型的输出用于决策时,调整决策阈值尤为重要。此外,用于调整决策阈值的指标应谨慎选择。这里我们使用了平衡准确率,但它可能不是最适合当前问题的指标。选择“正确”的指标通常依赖于具体问题,并可能需要一些领域知识。有关更多详细信息,请参阅标题为 调整决策阈值以适应成本敏感学习 的示例。
Total running time of the script: (0 minutes 12.038 seconds)
Related examples