Note

Go to the end to download the full example code. or to run this example in your browser via Binder

二维嵌入数字的各种凝聚聚类#

在数字数据集的二维嵌入上展示各种凝聚聚类的链接选项。

此示例的目的是直观地展示度量的行为，而不是为数字数据集找到好的聚类。这就是为什么示例在二维嵌入上进行。

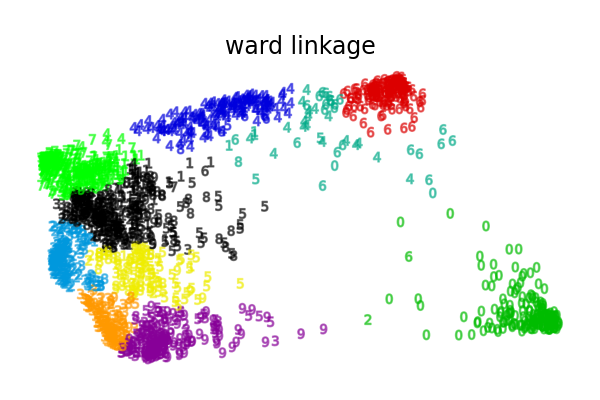
这个示例向我们展示了凝聚聚类的“富者愈富”行为，倾向于创建不均匀的聚类大小。

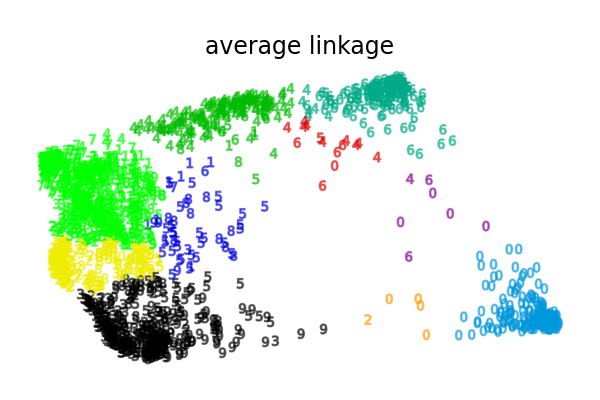
这种行为在平均链接策略中尤为明显，最终会形成几个数据点较少的聚类。

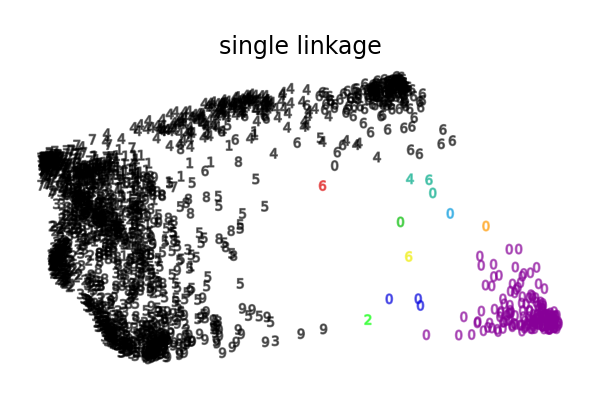
单链接的情况甚至更为病态，形成一个覆盖大多数数字的非常大的聚类，一个中等大小（干净）的聚类包含大多数零数字，其他所有聚类则由边缘噪声点组成。

其他链接策略导致更均匀分布的聚类，因此更不容易受到数据集随机重采样的影响。

Computing embedding
Done.
ward :  0.04s
average :       0.02s
complete :      0.02s
single :        0.04s

# 作者：scikit-learn 开发者
# SPDX-License-Identifier: BSD-3-Clause

from time import time

import numpy as np
from matplotlib import pyplot as plt

from sklearn import datasets, manifold

digits = datasets.load_digits()
X, y = digits.data, digits.target
n_samples, n_features = X.shape

np.random.seed(0)


# ----------------------------------------------------------------------
# 可视化聚类
def plot_clustering(X_red, labels, title=None):
    x_min, x_max = np.min(X_red, axis=0), np.max(X_red, axis=0)
    X_red = (X_red - x_min) / (x_max - x_min)

    plt.figure(figsize=(6, 4))
    for digit in digits.target_names:
        plt.scatter(
            *X_red[y == digit].T,
            marker=f"${digit}$",
            s=50,
            c=plt.cm.nipy_spectral(labels[y == digit] / 10),
            alpha=0.5,
        )

    plt.xticks([])
    plt.yticks([])
    if title is not None:
        plt.title(title, size=17)
    plt.axis("off")
    plt.tight_layout(rect=[0, 0.03, 1, 0.95])


# ----------------------------------------------------------------------
# 数字数据集的二维嵌入
print("Computing embedding")
X_red = manifold.SpectralEmbedding(n_components=2).fit_transform(X)
print("Done.")

from sklearn.cluster import AgglomerativeClustering

for linkage in ("ward", "average", "complete", "single"):
    clustering = AgglomerativeClustering(linkage=linkage, n_clusters=10)
    t0 = time()
    clustering.fit(X_red)
    print("%s :\t%.2fs" % (linkage, time() - t0))

    plot_clustering(X_red, clustering.labels_, "%s linkage" % linkage)


plt.show()