Note

Go to the end to download the full example code. or to run this example in your browser via Binder

单一估计器与袋装法：偏差-方差分解#

这个例子说明并比较了单一估计器与袋装集成的期望均方误差的偏差-方差分解。

在回归中，估计器的期望均方误差可以分解为偏差、方差和噪声。在回归问题的数据集上平均，偏差项衡量估计器的预测与问题的最佳可能估计器（即贝叶斯模型）的预测之间的平均差异。方差项衡量估计器在不同随机实例上的预测的可变性。每个问题实例在下文中记为“LS”，即“学习样本”。最后，噪声衡量的是由于数据的可变性而导致的误差中不可减少的部分。

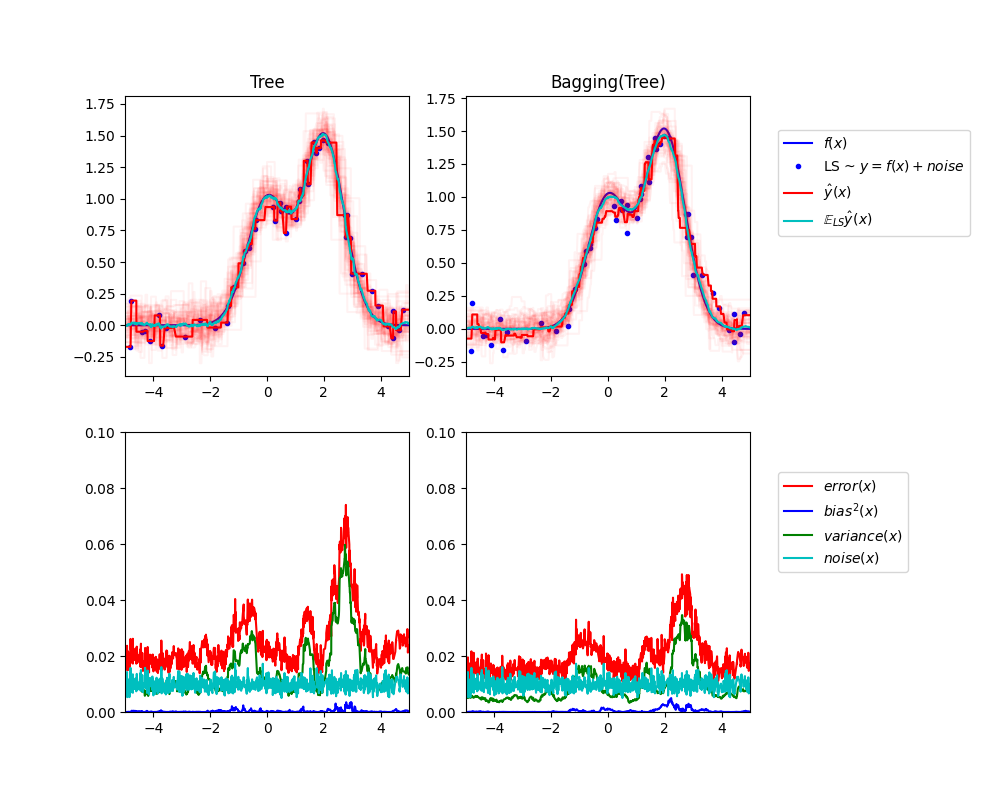
左上图展示了在一个玩具1d回归问题的随机数据集LS（蓝点）上训练的单一决策树的预测（深红色）。它还展示了在问题的其他（且不同的）随机抽取实例LS上训练的其他单一决策树的预测（浅红色）。直观上，这里的方差项对应于单个估计器的预测束（浅红色）的宽度。方差越大，预测对训练集的小变化越敏感。偏差项对应于估计器的平均预测（青色）与最佳可能模型（深蓝色）之间的差异。在这个问题上，我们可以观察到偏差相当低（青色和蓝色曲线彼此接近），而方差很大（红色束相当宽）。

左下图绘制了单一决策树的期望均方误差的逐点分解。它确认了偏差项（蓝色）很低，而方差很大（绿色）。它还展示了误差的噪声部分，正如预期的那样，噪声似乎是恒定的，大约为 0.01 。

右图对应于相同的图，但使用的是决策树的袋装集成。在这两幅图中，我们可以观察到偏差项比前一种情况更大。在右上图中，平均预测（青色）与最佳可能模型之间的差异更大（例如，注意 x=2 附近的偏移）。在右下图中，偏差曲线也比左下图稍高。然而，在方差方面，预测束更窄，这表明方差较低。确实，如右下图所确认的，方差项（绿色）比单一决策树低。总体而言，偏差-方差分解不再相同。袋装法的权衡更好：对数据集的自助法副本拟合的多个决策树的平均略微增加了偏差项，但允许大幅减少方差，从而导致较低的总体均方误差（比较下图中的红色曲线）。脚本输出也证实了这一直觉。袋装集成的总误差低于单一决策树的总误差，这种差异确实主要来自于方差的减少。

有关偏差-方差分解的更多详细信息，请参见[1]_的第7.3节。

参考文献#

Tree: 0.0255 (error) = 0.0003 (bias^2)  + 0.0152 (var) + 0.0098 (noise)
Bagging(Tree): 0.0196 (error) = 0.0004 (bias^2)  + 0.0092 (var) + 0.0098 (noise)

# 作者：scikit-learn 开发者
# SPDX-License-Identifier：BSD-3-Clause

import matplotlib.pyplot as plt
import numpy as np

from sklearn.ensemble import BaggingRegressor
from sklearn.tree import DecisionTreeRegressor

# Settings
n_repeat = 50  # Number of iterations for computing expectations
n_train = 50  # Size of the training set
n_test = 1000  # Size of the test set
noise = 0.1  # Standard deviation of the noise
np.random.seed(0)

# 更改此项以探索其他估计器的偏差-方差分解。对于高方差的估计器（例如，决策树或KNN），这应该效果很好，但对于低方差的估计器（例如，线性模型），效果较差。
estimators = [
    ("Tree", DecisionTreeRegressor()),
    ("Bagging(Tree)", BaggingRegressor(DecisionTreeRegressor())),
]

n_estimators = len(estimators)


# 生成数据
def f(x):
    x = x.ravel()

    return np.exp(-(x**2)) + 1.5 * np.exp(-((x - 2) ** 2))


def generate(n_samples, noise, n_repeat=1):
    X = np.random.rand(n_samples) * 10 - 5
    X = np.sort(X)

    if n_repeat == 1:
        y = f(X) + np.random.normal(0.0, noise, n_samples)
    else:
        y = np.zeros((n_samples, n_repeat))

        for i in range(n_repeat):
            y[:, i] = f(X) + np.random.normal(0.0, noise, n_samples)

    X = X.reshape((n_samples, 1))

    return X, y


X_train = []
y_train = []

for i in range(n_repeat):
    X, y = generate(n_samples=n_train, noise=noise)
    X_train.append(X)
    y_train.append(y)

X_test, y_test = generate(n_samples=n_test, noise=noise, n_repeat=n_repeat)

plt.figure(figsize=(10, 8))

# 循环遍历估计器以进行比较
for n, (name, estimator) in enumerate(estimators):
    # Compute predictions
    y_predict = np.zeros((n_test, n_repeat))

    for i in range(n_repeat):
        estimator.fit(X_train[i], y_train[i])
        y_predict[:, i] = estimator.predict(X_test)

    # 均方误差的偏差平方 + 方差 + 噪声分解
    y_error = np.zeros(n_test)

    for i in range(n_repeat):
        for j in range(n_repeat):
            y_error += (y_test[:, j] - y_predict[:, i]) ** 2

    y_error /= n_repeat * n_repeat

    y_noise = np.var(y_test, axis=1)
    y_bias = (f(X_test) - np.mean(y_predict, axis=1)) ** 2
    y_var = np.var(y_predict, axis=1)

    print(
        "{0}: {1:.4f} (error) = {2:.4f} (bias^2) "
        " + {3:.4f} (var) + {4:.4f} (noise)".format(
            name, np.mean(y_error), np.mean(y_bias), np.mean(y_var), np.mean(y_noise)
        )
    )

    # Plot figures
    plt.subplot(2, n_estimators, n + 1)
    plt.plot(X_test, f(X_test), "b", label="$f(x)$")
    plt.plot(X_train[0], y_train[0], ".b", label="LS ~ $y = f(x)+noise$")

    for i in range(n_repeat):
        if i == 0:
            plt.plot(X_test, y_predict[:, i], "r", label=r"$\^y(x)$")
        else:
            plt.plot(X_test, y_predict[:, i], "r", alpha=0.05)

    plt.plot(X_test, np.mean(y_predict, axis=1), "c", label=r"$\mathbb{E}_{LS} \^y(x)$")

    plt.xlim([-5, 5])
    plt.title(name)

    if n == n_estimators - 1:
        plt.legend(loc=(1.1, 0.5))

    plt.subplot(2, n_estimators, n_estimators + n + 1)
    plt.plot(X_test, y_error, "r", label="$error(x)$")
    plt.plot(X_test, y_bias, "b", label="$bias^2(x)$"),
    plt.plot(X_test, y_var, "g", label="$variance(x)$"),
    plt.plot(X_test, y_noise, "c", label="$noise(x)$")

    plt.xlim([-5, 5])
    plt.ylim([0, 0.1])

    if n == n_estimators - 1:
        plt.legend(loc=(1.1, 0.5))

plt.subplots_adjust(right=0.75)
plt.show()