Note

Go to the end to download the full example code. or to run this example in your browser via Binder

k-means 假设的演示#

此示例旨在说明 k-means 产生非直观且可能不理想的聚类的情况。

# 作者：scikit-learn 开发者
# SPDX 许可证标识符：BSD-3-Clause

数据生成#

函数 make_blobs 生成各向同性（球形）的高斯斑点。要获得各向异性（椭圆形）的高斯斑点，需要定义一个线性 变换 。

import numpy as np

from sklearn.datasets import make_blobs

n_samples = 1500
random_state = 170
transformation = [[0.60834549, -0.63667341], [-0.40887718, 0.85253229]]

X, y = make_blobs(n_samples=n_samples, random_state=random_state)
X_aniso = np.dot(X, transformation)  # Anisotropic blobs
X_varied, y_varied = make_blobs(
    n_samples=n_samples, cluster_std=[1.0, 2.5, 0.5], random_state=random_state
)  # Unequal variance
X_filtered = np.vstack(
    (X[y == 0][:500], X[y == 1][:100], X[y == 2][:10])
)  # Unevenly sized blobs
y_filtered = [0] * 500 + [1] * 100 + [2] * 10

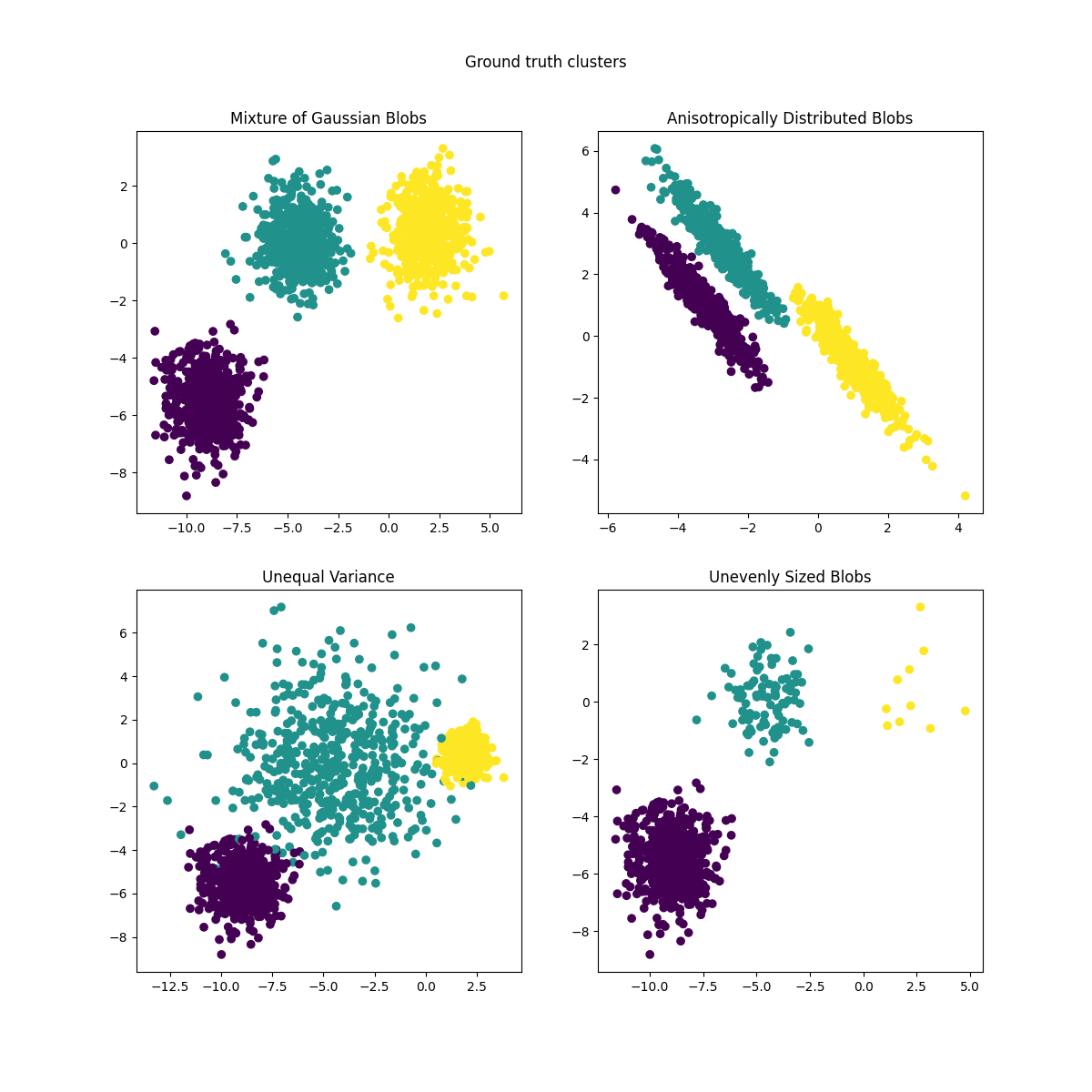
我们可以将结果数据可视化：

import matplotlib.pyplot as plt

fig, axs = plt.subplots(nrows=2, ncols=2, figsize=(12, 12))

axs[0, 0].scatter(X[:, 0], X[:, 1], c=y)
axs[0, 0].set_title("Mixture of Gaussian Blobs")

axs[0, 1].scatter(X_aniso[:, 0], X_aniso[:, 1], c=y)
axs[0, 1].set_title("Anisotropically Distributed Blobs")

axs[1, 0].scatter(X_varied[:, 0], X_varied[:, 1], c=y_varied)
axs[1, 0].set_title("Unequal Variance")

axs[1, 1].scatter(X_filtered[:, 0], X_filtered[:, 1], c=y_filtered)
axs[1, 1].set_title("Unevenly Sized Blobs")

plt.suptitle("Ground truth clusters").set_y(0.95)
plt.show()

Ground truth clusters, Mixture of Gaussian Blobs, Anisotropically Distributed Blobs, Unequal Variance, Unevenly Sized Blobs

拟合模型并绘制结果#

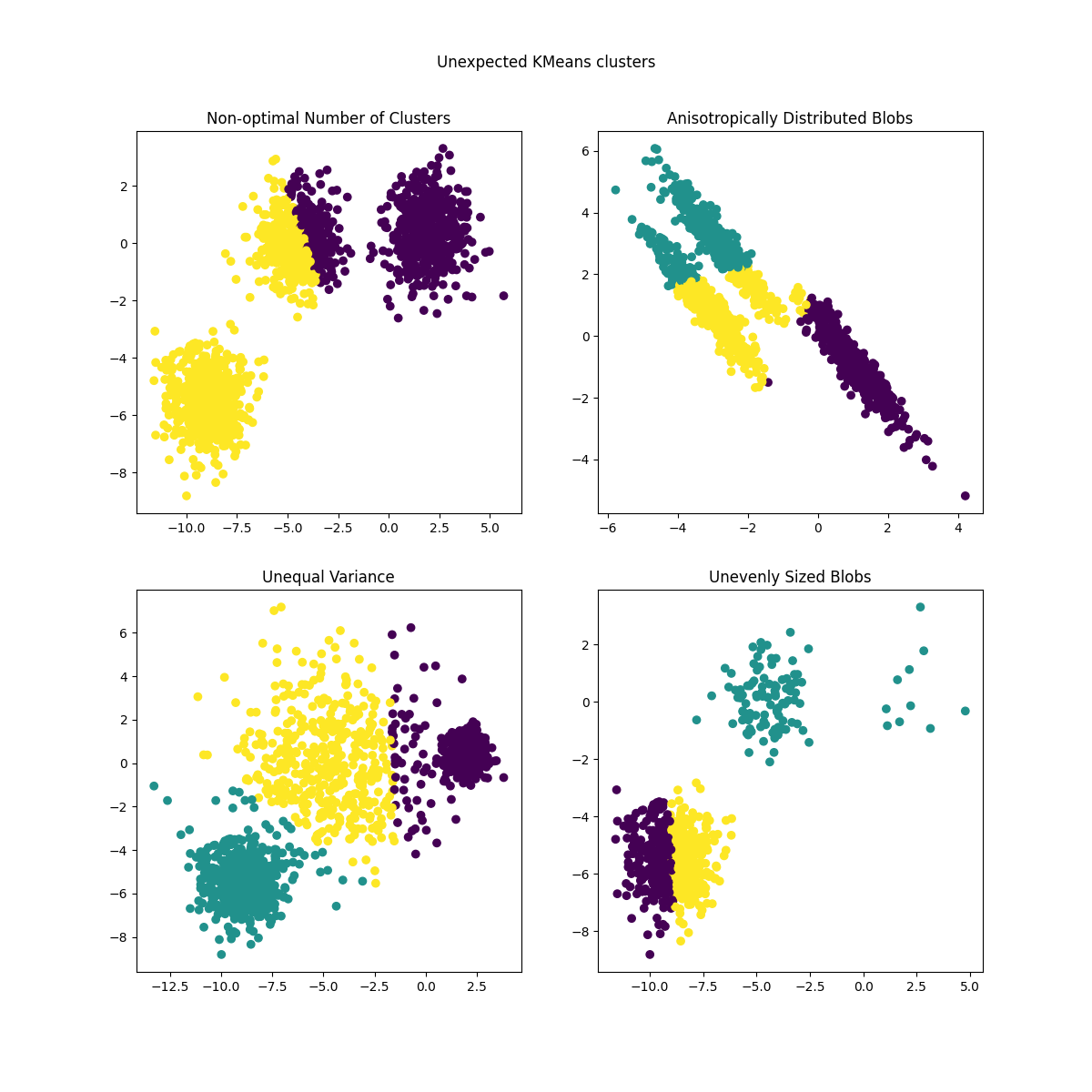
之前生成的数据现在用于展示 KMeans 在以下场景中的表现：

非最优的聚类数量：在实际情况下，没有唯一定义的真正聚类数量。适当的聚类数量需要根据数据标准和预期目标来决定。
各向异性分布的斑点：k-means通过最小化样本到其分配的聚类中心的欧几里得距离来工作。因此，k-means更适用于各向同性且正态分布的聚类（即球形高斯分布）。
不同的方差：k-means等价于对具有相同方差但均值可能不同的k个高斯分布的“混合”进行最大似然估计。
不均匀大小的斑点：没有关于k-means的理论结果表明它需要相似的聚类大小才能表现良好，但最小化欧几里得距离意味着问题越稀疏且维度越高，就越需要使用不同的聚类中心种子运行算法以确保全局最小惯性。

from sklearn.cluster import KMeans

common_params = {
    "n_init": "auto",
    "random_state": random_state,
}

fig, axs = plt.subplots(nrows=2, ncols=2, figsize=(12, 12))

y_pred = KMeans(n_clusters=2, **common_params).fit_predict(X)
axs[0, 0].scatter(X[:, 0], X[:, 1], c=y_pred)
axs[0, 0].set_title("Non-optimal Number of Clusters")

y_pred = KMeans(n_clusters=3, **common_params).fit_predict(X_aniso)
axs[0, 1].scatter(X_aniso[:, 0], X_aniso[:, 1], c=y_pred)
axs[0, 1].set_title("Anisotropically Distributed Blobs")

y_pred = KMeans(n_clusters=3, **common_params).fit_predict(X_varied)
axs[1, 0].scatter(X_varied[:, 0], X_varied[:, 1], c=y_pred)
axs[1, 0].set_title("Unequal Variance")

y_pred = KMeans(n_clusters=3, **common_params).fit_predict(X_filtered)
axs[1, 1].scatter(X_filtered[:, 0], X_filtered[:, 1], c=y_pred)
axs[1, 1].set_title("Unevenly Sized Blobs")

plt.suptitle("Unexpected KMeans clusters").set_y(0.95)
plt.show()

Unexpected KMeans clusters, Non-optimal Number of Clusters, Anisotropically Distributed Blobs, Unequal Variance, Unevenly Sized Blobs

可能的解决方案#

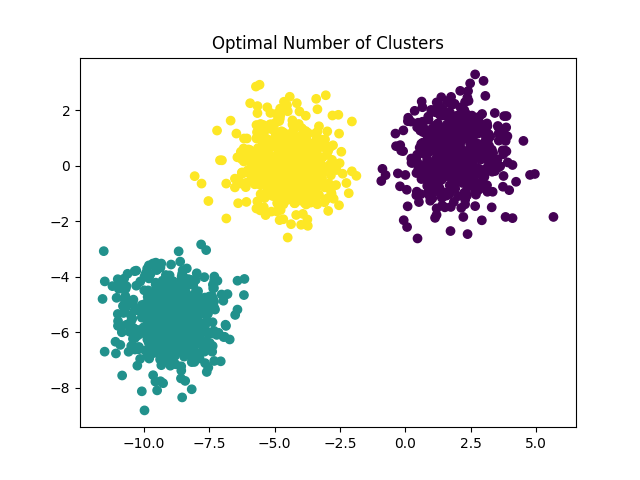
要了解如何找到正确的簇数量，请参见使用轮廓分析选择KMeans聚类的簇数。在这种情况下，将 n_clusters 设置为 3 即可。

y_pred = KMeans(n_clusters=3, **common_params).fit_predict(X)
plt.scatter(X[:, 0], X[:, 1], c=y_pred)
plt.title("Optimal Number of Clusters")
plt.show()

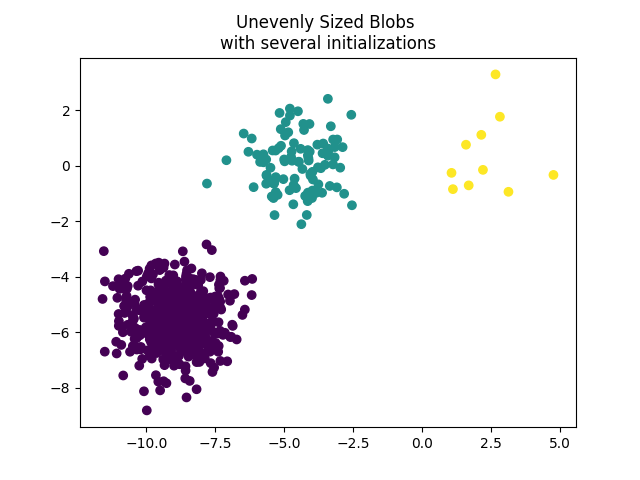
为了处理大小不均匀的斑点，可以增加随机初始化的次数。在这种情况下，我们设置 n_init=10 以避免找到次优的局部最小值。更多细节请参见使用k-means对稀疏数据进行聚类。

y_pred = KMeans(n_clusters=3, n_init=10, random_state=random_state).fit_predict(
    X_filtered
)
plt.scatter(X_filtered[:, 0], X_filtered[:, 1], c=y_pred)
plt.title("Unevenly Sized Blobs \nwith several initializations")
plt.show()

Unevenly Sized Blobs with several initializations

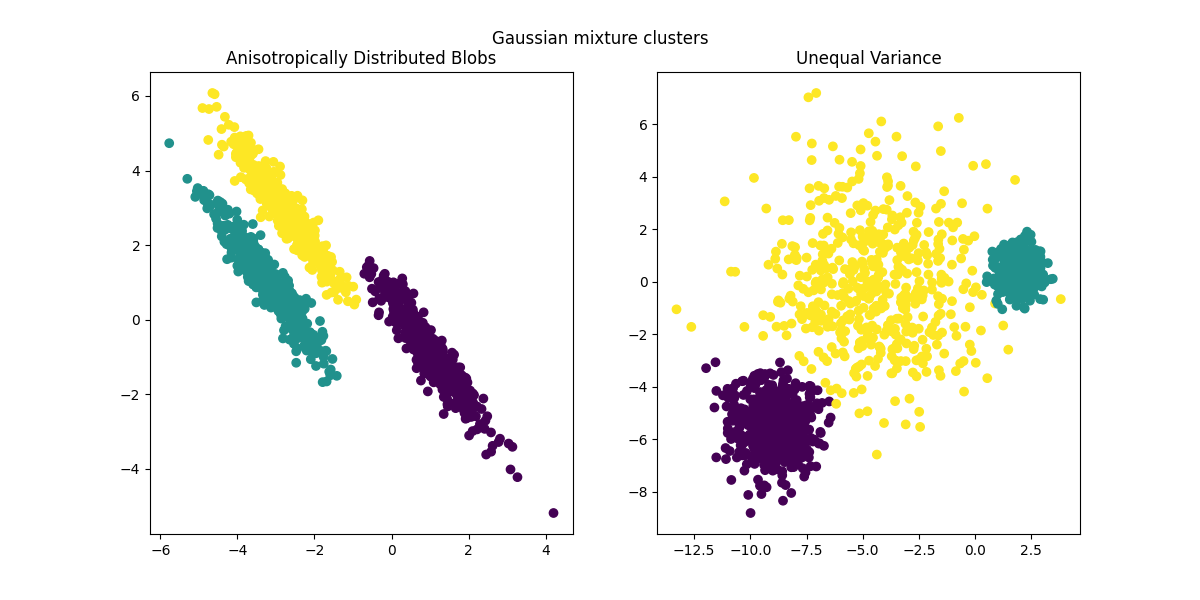
由于各向异性和不等方差是 k-means 算法的实际限制，这里我们建议使用 GaussianMixture ，它同样假设高斯簇，但不对其方差施加任何约束。请注意，仍然需要找到正确的簇数（参见高斯混合模型选择）。

关于其他聚类方法如何处理各向异性或不等方差的簇的示例，请参见示例在玩具数据集上比较不同的聚类算法。

from sklearn.mixture import GaussianMixture

fig, (ax1, ax2) = plt.subplots(nrows=1, ncols=2, figsize=(12, 6))

y_pred = GaussianMixture(n_components=3).fit_predict(X_aniso)
ax1.scatter(X_aniso[:, 0], X_aniso[:, 1], c=y_pred)
ax1.set_title("Anisotropically Distributed Blobs")

y_pred = GaussianMixture(n_components=3).fit_predict(X_varied)
ax2.scatter(X_varied[:, 0], X_varied[:, 1], c=y_pred)
ax2.set_title("Unequal Variance")

plt.suptitle("Gaussian mixture clusters").set_y(0.95)
plt.show()