Note

Go to the end to download the full example code. or to run this example in your browser via Binder

带有和不带有结构的凝聚聚类#

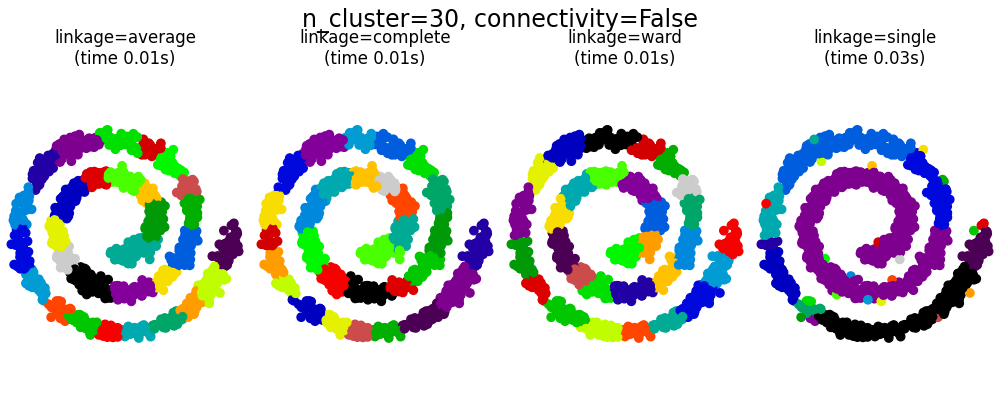
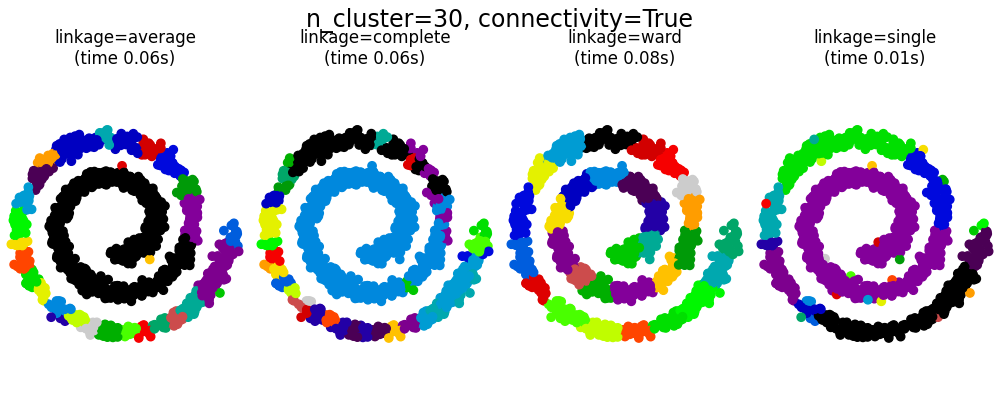
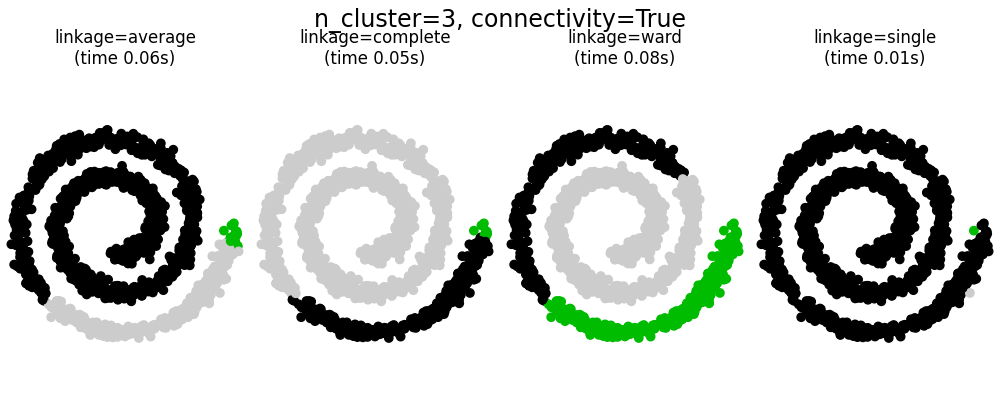
此示例展示了施加连接图以捕捉数据中的局部结构的效果。该图只是20个最近邻的图。

施加连接性的好处有两个。首先，使用稀疏连接矩阵进行聚类通常更快。

其次，当使用连接矩阵时，单一、平均和完全链接是不稳定的，往往会创建一些快速增长的簇。实际上，平均和完全链接通过在合并簇时考虑两个簇之间的所有距离来对抗这种渗透行为（而单一链接通过仅考虑簇之间的最短距离来夸大这种行为）。连接图打破了这种机制，使平均和完全链接更像脆弱的单一链接。这种效果在非常稀疏的图中更为明显（尝试减少kneighbors_graph中的邻居数量）并且在完全链接中尤为显著。特别是，在图中有非常少的邻居数量时，会强加一种接近单一链接的几何结构，而单一链接是众所周知的具有这种渗透不稳定性的。

# 作者：scikit-learn 开发者
# SPDX-License-Identifier: BSD-3-Clause

import time

import matplotlib.pyplot as plt
import numpy as np

from sklearn.cluster import AgglomerativeClustering
from sklearn.neighbors import kneighbors_graph

# 生成示例数据
n_samples = 1500
np.random.seed(0)
t = 1.5 * np.pi * (1 + 3 * np.random.rand(1, n_samples))
x = t * np.cos(t)
y = t * np.sin(t)


X = np.concatenate((x, y))
X += 0.7 * np.random.randn(2, n_samples)
X = X.T

# 创建一个捕捉局部连通性的图。更多的邻居数量将会形成更均匀的簇，但会增加计算时间。非常多的邻居数量会使簇的大小分布更加均匀，但可能无法体现数据的局部流形结构。
knn_graph = kneighbors_graph(X, 30, include_self=False)

for connectivity in (None, knn_graph):
    for n_clusters in (30, 3):
        plt.figure(figsize=(10, 4))
        for index, linkage in enumerate(("average", "complete", "ward", "single")):
            plt.subplot(1, 4, index + 1)
            model = AgglomerativeClustering(
                linkage=linkage, connectivity=connectivity, n_clusters=n_clusters
            )
            t0 = time.time()
            model.fit(X)
            elapsed_time = time.time() - t0
            plt.scatter(X[:, 0], X[:, 1], c=model.labels_, cmap=plt.cm.nipy_spectral)
            plt.title(
                "linkage=%s\n(time %.2fs)" % (linkage, elapsed_time),
                fontdict=dict(verticalalignment="top"),
            )
            plt.axis("equal")
            plt.axis("off")

            plt.subplots_adjust(bottom=0, top=0.83, wspace=0, left=0, right=1)
            plt.suptitle(
                "n_cluster=%i, connectivity=%r"
                % (n_clusters, connectivity is not None),
                size=17,
            )


plt.show()