Note
Go to the end to download the full example code. or to run this example in your browser via Binder
Tweedie回归在保险理赔中的应用#
本示例展示了在 French Motor Third-Party Liability Claims dataset 上使用泊松、伽马和Tweedie回归的应用,灵感来自于一个R教程[1]_。
在这个数据集中,每个样本对应一个保险单,即保险公司与个人(投保人)之间的合同。可用特征包括驾驶员年龄、车辆年龄、车辆功率等。
一些定义:*理赔*是投保人向保险公司提出的赔偿损失的请求。*理赔金额*是保险公司必须支付的金额。*暴露*是给定保单的保险覆盖期限,以年为单位。
这里我们的目标是预测每个暴露单位的总理赔金额的期望值,即平均值,也称为纯保费。
有几种方法可以实现这一目标,其中两种是:
使用泊松分布对理赔次数建模,并使用伽马分布对每次理赔的平均理赔金额(也称为严重度)建模,然后将两者的预测结果相乘以获得总理赔金额。
直接对每个暴露单位的总理赔金额建模,通常使用Tweedie分布,Tweedie幂 \(p \in (1, 2)\) 。
在本示例中,我们将展示这两种方法。我们首先定义一些辅助函数来加载数据和可视化结果。
from functools import partial
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn.datasets import fetch_openml
from sklearn.metrics import (
mean_absolute_error,
mean_squared_error,
mean_tweedie_deviance,
)
def load_mtpl2(n_samples=None):
"""获取法国机动车第三方责任索赔数据集。
Parameters
----------
n_samples: int, 默认值=None
要选择的样本数量(以加快运行时间)。完整数据集有678013个样本。
"""
# freMTPL2freq 数据集来自 https://www.openml.org/d/41214
df_freq = fetch_openml(data_id=41214, as_frame=True).data
df_freq["IDpol"] = df_freq["IDpol"].astype(int)
df_freq.set_index("IDpol", inplace=True)
# freMTPL2sev 数据集来自 https://www.openml.org/d/41215
df_sev = fetch_openml(data_id=41215, as_frame=True).data
# 对相同ID的ClaimAmount求和
df_sev = df_sev.groupby("IDpol").sum()
df = df_freq.join(df_sev, how="left")
df["ClaimAmount"] = df["ClaimAmount"].fillna(0)
# unquote string fields
for column_name in df.columns[df.dtypes.values == object]:
df[column_name] = df[column_name].str.strip("'")
return df.iloc[:n_samples]
def plot_obs_pred(
df,
feature,
weight,
observed,
predicted,
y_label=None,
title=None,
ax=None,
fill_legend=False,
):
"""绘制每个特征级别聚合的观测值和预测值。
Parameters
----------
df : DataFrame
输入数据
feature: str
要绘制的df中的列名
weight : str
df中包含权重或暴露值的列名
observed : str
df中包含观测目标的列名
predicted : DataFrame
与df具有相同索引的包含预测目标的数据框
fill_legend : bool, 默认=False
是否显示fill_between图例
"""
# 按特征级别汇总观察到的和预测的变量
df_ = df.loc[:, [feature, weight]].copy()
df_["observed"] = df[observed] * df[weight]
df_["predicted"] = predicted * df[weight]
df_ = (
df_.groupby([feature])[[weight, "observed", "predicted"]]
.sum()
.assign(observed=lambda x: x["observed"] / x[weight])
.assign(predicted=lambda x: x["predicted"] / x[weight])
)
ax = df_.loc[:, ["observed", "predicted"]].plot(style=".", ax=ax)
y_max = df_.loc[:, ["observed", "predicted"]].values.max() * 0.8
p2 = ax.fill_between(
df_.index,
0,
y_max * df_[weight] / df_[weight].values.max(),
color="g",
alpha=0.1,
)
if fill_legend:
ax.legend([p2], ["{} distribution".format(feature)])
ax.set(
ylabel=y_label if y_label is not None else None,
title=title if title is not None else "Train: Observed vs Predicted",
)
def score_estimator(
estimator,
X_train,
X_test,
df_train,
df_test,
target,
weights,
tweedie_powers=None,
):
"""在训练集和测试集上使用不同的指标评估估计器"""
metrics = [
("D² explained", None), # Use default scorer if it exists
("mean abs. error", mean_absolute_error),
("mean squared error", mean_squared_error),
]
if tweedie_powers:
metrics += [
(
"mean Tweedie dev p={:.4f}".format(power),
partial(mean_tweedie_deviance, power=power),
)
for power in tweedie_powers
]
res = []
for subset_label, X, df in [
("train", X_train, df_train),
("test", X_test, df_test),
]:
y, _weights = df[target], df[weights]
for score_label, metric in metrics:
if isinstance(estimator, tuple) and len(estimator) == 2:
# 对由频率模型和严重性模型的乘积组成的模型进行评分。
est_freq, est_sev = estimator
y_pred = est_freq.predict(X) * est_sev.predict(X)
else:
y_pred = estimator.predict(X)
if metric is None:
if not hasattr(estimator, "score"):
continue
score = estimator.score(X, y, sample_weight=_weights)
else:
score = metric(y, y_pred, sample_weight=_weights)
res.append({"subset": subset_label, "metric": score_label, "score": score})
res = (
pd.DataFrame(res)
.set_index(["metric", "subset"])
.score.unstack(-1)
.round(4)
.loc[:, ["train", "test"]]
)
return res
加载数据集、基本特征提取和目标定义#
我们通过将包含索赔次数( ClaimNb )的 freMTPL2freq 表与包含相同保单 ID( IDpol )的索赔金额( ClaimAmount )的 freMTPL2sev 表连接起来,构建了 freMTPL2 数据集。
from sklearn.compose import ColumnTransformer
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import (
FunctionTransformer,
KBinsDiscretizer,
OneHotEncoder,
StandardScaler,
)
df = load_mtpl2()
# 修正不合理的观测值(可能是数据错误)和一些异常大的索赔金额
df["ClaimNb"] = df["ClaimNb"].clip(upper=4)
df["Exposure"] = df["Exposure"].clip(upper=1)
df["ClaimAmount"] = df["ClaimAmount"].clip(upper=200000)
# 如果索赔金额为0,则我们不将其视为索赔。严重性模型使用的损失函数需要严格为正的索赔金额。这样,频率和严重性之间更加一致。
df.loc[(df["ClaimAmount"] == 0) & (df["ClaimNb"] >= 1), "ClaimNb"] = 0
log_scale_transformer = make_pipeline(
FunctionTransformer(func=np.log), StandardScaler()
)
column_trans = ColumnTransformer(
[
(
"binned_numeric",
KBinsDiscretizer(n_bins=10, random_state=0),
["VehAge", "DrivAge"],
),
(
"onehot_categorical",
OneHotEncoder(),
["VehBrand", "VehPower", "VehGas", "Region", "Area"],
),
("passthrough_numeric", "passthrough", ["BonusMalus"]),
("log_scaled_numeric", log_scale_transformer, ["Density"]),
],
remainder="drop",
)
X = column_trans.fit_transform(df)
# 保险公司对纯保费的建模很感兴趣,即每个保单持有人在其风险暴露单位上的预期总赔付金额:
df["PurePremium"] = df["ClaimAmount"] / df["Exposure"]
# 这可以通过两步建模间接近似:频率乘以每次索赔的平均索赔金额:
df["Frequency"] = df["ClaimNb"] / df["Exposure"]
df["AvgClaimAmount"] = df["ClaimAmount"] / np.fmax(df["ClaimNb"], 1)
with pd.option_context("display.max_columns", 15):
print(df[df.ClaimAmount > 0].head())
ClaimNb Exposure Area VehPower VehAge DrivAge BonusMalus VehBrand \
IDpol
139 1 0.75 F 7 1 61 50 B12
190 1 0.14 B 12 5 50 60 B12
414 1 0.14 E 4 0 36 85 B12
424 2 0.62 F 10 0 51 100 B12
463 1 0.31 A 5 0 45 50 B12
VehGas Density Region ClaimAmount PurePremium Frequency \
IDpol
139 Regular 27000 R11 303.00 404.000000 1.333333
190 Diesel 56 R25 1981.84 14156.000000 7.142857
414 Regular 4792 R11 1456.55 10403.928571 7.142857
424 Regular 27000 R11 10834.00 17474.193548 3.225806
463 Regular 12 R73 3986.67 12860.225806 3.225806
AvgClaimAmount
IDpol
139 303.00
190 1981.84
414 1456.55
424 5417.00
463 3986.67
频率模型 – 泊松分布#
索赔数量( ClaimNb )是一个正整数(包括0)。因此,该目标可以用泊松分布建模。假设它是在给定时间间隔(以年为单位的 Exposure )内以恒定速率发生的离散事件的数量。在这里,我们建模频率 y = ClaimNb / Exposure ,这仍然是一个(缩放的)泊松分布,并使用 Exposure 作为 sample_weight 。
from sklearn.linear_model import PoissonRegressor
from sklearn.model_selection import train_test_split
df_train, df_test, X_train, X_test = train_test_split(df, X, random_state=0)
请记住,尽管此数据集中看似有大量的数据点,但索赔金额不为零的评估点数量却相当少:
len(df_test)
169504
len(df_test[df_test["ClaimAmount"] > 0])
6237
因此,我们预计在随机重新抽样训练测试拆分时,我们的评估结果会有显著的变异性。
通过牛顿求解器在训练集上最小化泊松偏差来估计模型的参数。由于某些特征是共线的(例如,因为我们在 OneHotEncoder 中没有删除任何分类级别),我们使用弱L2惩罚来避免数值问题。
glm_freq = PoissonRegressor(alpha=1e-4, solver="newton-cholesky")
glm_freq.fit(X_train, df_train["Frequency"], sample_weight=df_train["Exposure"])
scores = score_estimator(
glm_freq,
X_train,
X_test,
df_train,
df_test,
target="Frequency",
weights="Exposure",
)
print("Evaluation of PoissonRegressor on target Frequency")
print(scores)
Evaluation of PoissonRegressor on target Frequency
subset train test
metric
D² explained 0.0448 0.0427
mean abs. error 0.1379 0.1378
mean squared error 0.2441 0.2246
请注意,在测试集上测得的分数竟然比训练集上的更好。这可能是由于这次随机的训练-测试集划分所致。适当的交叉验证可以帮助我们评估这些结果的抽样变异性。
我们可以通过驾驶员年龄( DrivAge )、车辆年龄( VehAge )和保险奖励/惩罚( BonusMalus )来汇总观察值和预测值,并进行直观比较。
fig, ax = plt.subplots(ncols=2, nrows=2, figsize=(16, 8))
fig.subplots_adjust(hspace=0.3, wspace=0.2)
plot_obs_pred(
df=df_train,
feature="DrivAge",
weight="Exposure",
observed="Frequency",
predicted=glm_freq.predict(X_train),
y_label="Claim Frequency",
title="train data",
ax=ax[0, 0],
)
plot_obs_pred(
df=df_test,
feature="DrivAge",
weight="Exposure",
observed="Frequency",
predicted=glm_freq.predict(X_test),
y_label="Claim Frequency",
title="test data",
ax=ax[0, 1],
fill_legend=True,
)
plot_obs_pred(
df=df_test,
feature="VehAge",
weight="Exposure",
observed="Frequency",
predicted=glm_freq.predict(X_test),
y_label="Claim Frequency",
title="test data",
ax=ax[1, 0],
fill_legend=True,
)
plot_obs_pred(
df=df_test,
feature="BonusMalus",
weight="Exposure",
observed="Frequency",
predicted=glm_freq.predict(X_test),
y_label="Claim Frequency",
title="test data",
ax=ax[1, 1],
fill_legend=True,
)
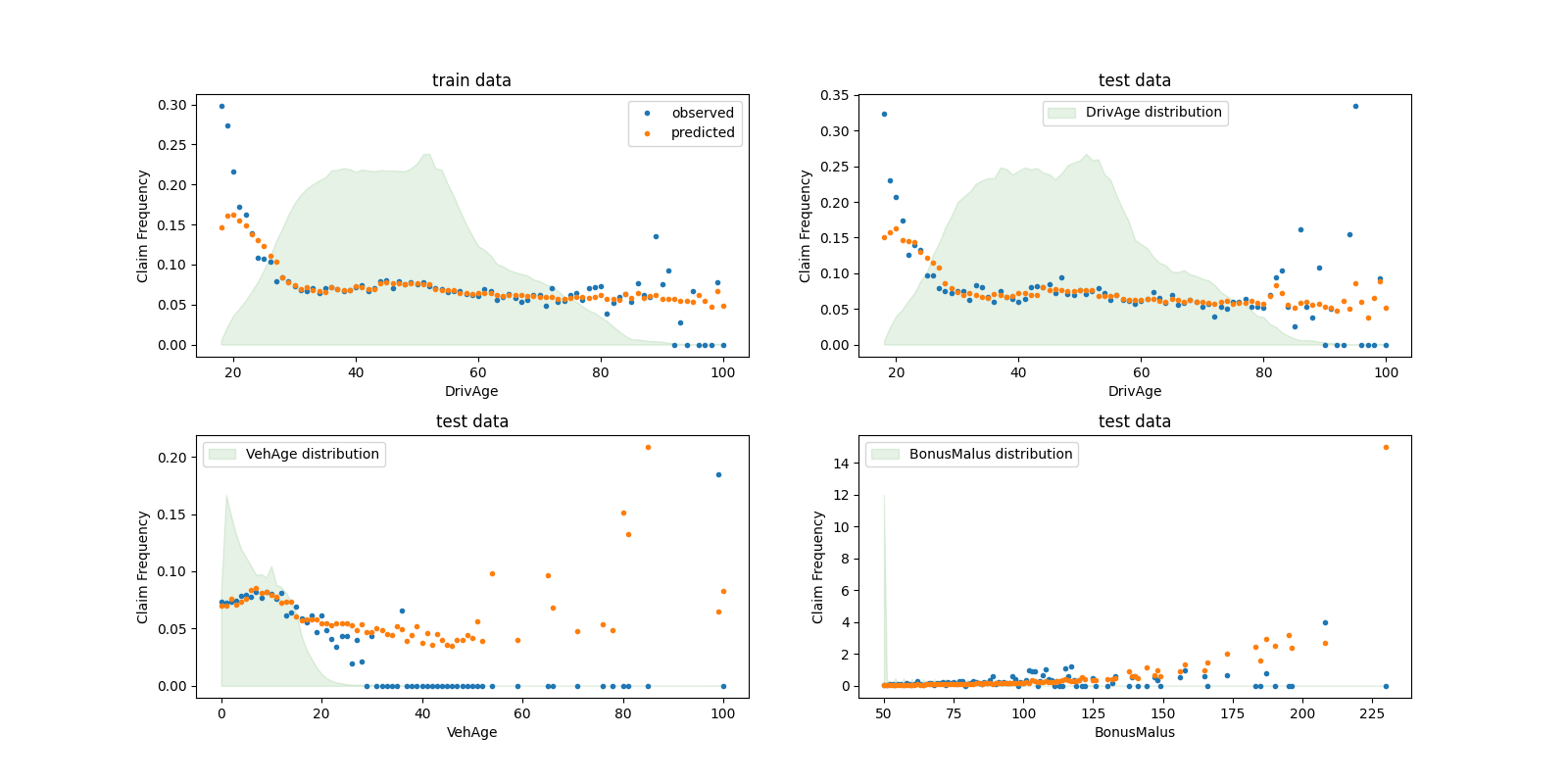
根据观察到的数据,30岁以下司机的事故频率较高,并且与 BonusMalus 变量呈正相关。我们的模型能够大致正确地模拟这种行为。
严重性模型 - 伽马分布#
平均索赔金额或严重性( AvgClaimAmount )可以通过经验表明大致遵循伽马分布。我们为严重性拟合了一个具有与频率模型相同特征的广义线性模型(GLM)。
Note:
我们过滤掉
ClaimAmount == 0,因为伽马分布的支持范围是 \((0, \infty)\) ,而不是 \([0, \infty)\) 。我们使用
ClaimNb作为sample_weight来考虑包含多个索赔的保单。
from sklearn.linear_model import GammaRegressor
mask_train = df_train["ClaimAmount"] > 0
mask_test = df_test["ClaimAmount"] > 0
glm_sev = GammaRegressor(alpha=10.0, solver="newton-cholesky")
glm_sev.fit(
X_train[mask_train.values],
df_train.loc[mask_train, "AvgClaimAmount"],
sample_weight=df_train.loc[mask_train, "ClaimNb"],
)
scores = score_estimator(
glm_sev,
X_train[mask_train.values],
X_test[mask_test.values],
df_train[mask_train],
df_test[mask_test],
target="AvgClaimAmount",
weights="ClaimNb",
)
print("Evaluation of GammaRegressor on target AvgClaimAmount")
print(scores)
Evaluation of GammaRegressor on target AvgClaimAmount
subset train test
metric
D² explained 3.900000e-03 4.400000e-03
mean abs. error 1.756746e+03 1.744042e+03
mean squared error 5.801770e+07 5.030677e+07
这些度量值的数值不一定容易解释。将它们与不使用任何输入特征且始终预测一个常数值(即相同设置下的平均索赔金额)的模型进行比较可能会很有启发性:
from sklearn.dummy import DummyRegressor
dummy_sev = DummyRegressor(strategy="mean")
dummy_sev.fit(
X_train[mask_train.values],
df_train.loc[mask_train, "AvgClaimAmount"],
sample_weight=df_train.loc[mask_train, "ClaimNb"],
)
scores = score_estimator(
dummy_sev,
X_train[mask_train.values],
X_test[mask_test.values],
df_train[mask_train],
df_test[mask_test],
target="AvgClaimAmount",
weights="ClaimNb",
)
print("Evaluation of a mean predictor on target AvgClaimAmount")
print(scores)
Evaluation of a mean predictor on target AvgClaimAmount
subset train test
metric
D² explained 0.000000e+00 -0.000000e+00
mean abs. error 1.756687e+03 1.744497e+03
mean squared error 5.803882e+07 5.033764e+07
我们得出结论,索赔金额非常难以预测。不过,GammaRegressor 能够利用输入特征中的一些信息,在 D² 方面略微优于均值基线。
请注意,所得模型是每次索赔的平均索赔金额。因此,它是以至少有一次索赔为条件的,不能用于预测每份保单的平均索赔金额。为此,需要将其与索赔频率模型结合使用。
print(
"Mean AvgClaim Amount per policy: %.2f "
% df_train["AvgClaimAmount"].mean()
)
print(
"Mean AvgClaim Amount | NbClaim > 0: %.2f"
% df_train["AvgClaimAmount"][df_train["AvgClaimAmount"] > 0].mean()
)
print(
"Predicted Mean AvgClaim Amount | NbClaim > 0: %.2f"
% glm_sev.predict(X_train).mean()
)
print(
"Predicted Mean AvgClaim Amount (dummy) | NbClaim > 0: %.2f"
% dummy_sev.predict(X_train).mean()
)
Mean AvgClaim Amount per policy: 71.78
Mean AvgClaim Amount | NbClaim > 0: 1951.21
Predicted Mean AvgClaim Amount | NbClaim > 0: 1940.95
Predicted Mean AvgClaim Amount (dummy) | NbClaim > 0: 1978.59
我们可以直观地比较按驾驶员年龄( DrivAge )汇总的观测值和预测值。
fig, ax = plt.subplots(ncols=1, nrows=2, figsize=(16, 6))
plot_obs_pred(
df=df_train.loc[mask_train],
feature="DrivAge",
weight="Exposure",
observed="AvgClaimAmount",
predicted=glm_sev.predict(X_train[mask_train.values]),
y_label="Average Claim Severity",
title="train data",
ax=ax[0],
)
plot_obs_pred(
df=df_test.loc[mask_test],
feature="DrivAge",
weight="Exposure",
observed="AvgClaimAmount",
predicted=glm_sev.predict(X_test[mask_test.values]),
y_label="Average Claim Severity",
title="test data",
ax=ax[1],
fill_legend=True,
)
plt.tight_layout()
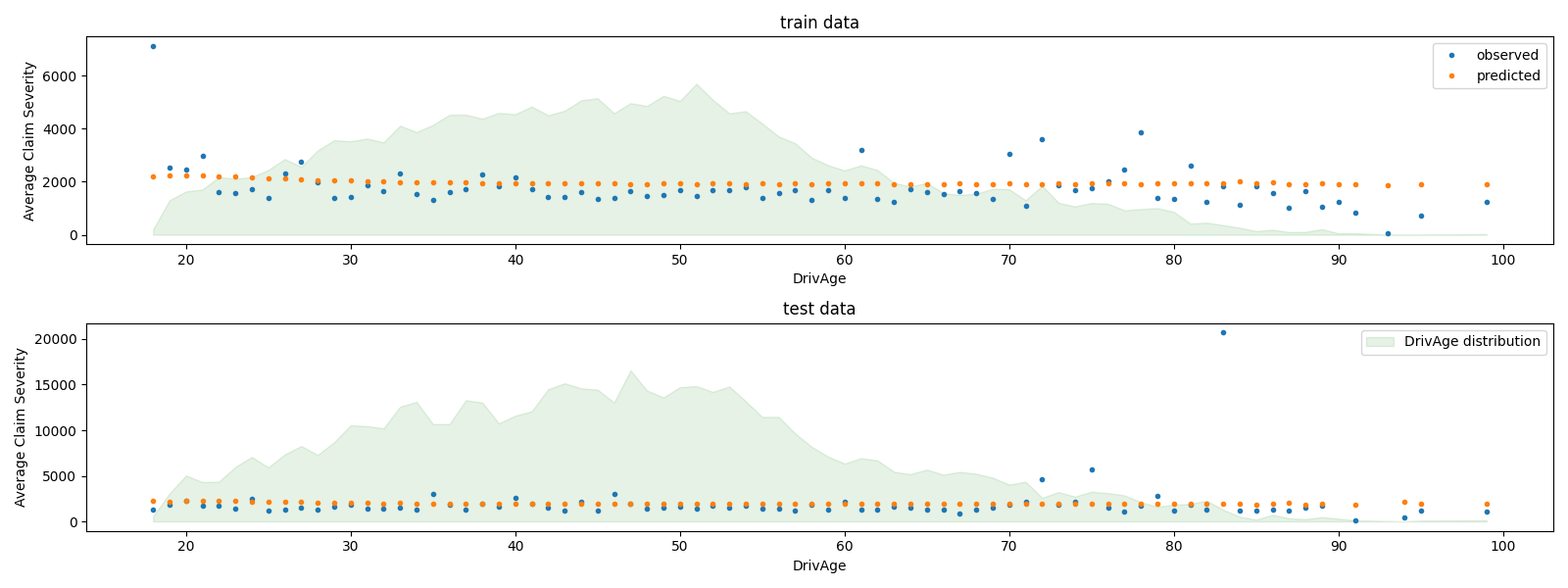
总体而言,无论是在观测数据还是预测数据中,驾驶员年龄( DrivAge )对理赔严重程度的影响都较弱。
纯保费建模:通过乘积模型与单一Tweedie回归模型的比较#
如介绍中所述,每单位暴露的总赔付金额可以建模为频率模型预测值与严重性模型预测值的乘积。
或者,可以直接使用独特的复合泊松伽马广义线性模型(带对数链接函数)来建模总损失。该模型是Tweedie GLM的一个特例,其“幂”参数 \(p \in (1, 2)\) 。在这里,我们先验地将Tweedie模型的“幂”参数固定为某个有效范围内的任意值(1.9)。理想情况下,可以通过网格搜索选择此值,以最小化Tweedie模型的负对数似然,但遗憾的是,目前的实现尚不允许这样做。
我们将比较两种方法的性能。
为了量化两种模型的性能,可以计算在假设总赔付金额服从复合泊松-伽马分布的情况下,训练数据和测试数据的平均偏差。这相当于一个 power 参数在 1 和 2 之间的 Tweedie 分布。
sklearn.metrics.mean_tweedie_deviance 依赖于 power 参数。由于我们不知道 power 参数的真实值,因此我们在这里计算一组可能值的平均偏差,并将模型并排比较,即在相同的 power 值下进行比较。理想情况下,我们希望一个模型在任何 power 值下都能始终优于另一个模型。
from sklearn.linear_model import TweedieRegressor
glm_pure_premium = TweedieRegressor(power=1.9, alpha=0.1, solver="newton-cholesky")
glm_pure_premium.fit(
X_train, df_train["PurePremium"], sample_weight=df_train["Exposure"]
)
tweedie_powers = [1.5, 1.7, 1.8, 1.9, 1.99, 1.999, 1.9999]
scores_product_model = score_estimator(
(glm_freq, glm_sev),
X_train,
X_test,
df_train,
df_test,
target="PurePremium",
weights="Exposure",
tweedie_powers=tweedie_powers,
)
scores_glm_pure_premium = score_estimator(
glm_pure_premium,
X_train,
X_test,
df_train,
df_test,
target="PurePremium",
weights="Exposure",
tweedie_powers=tweedie_powers,
)
scores = pd.concat(
[scores_product_model, scores_glm_pure_premium],
axis=1,
sort=True,
keys=("Product Model", "TweedieRegressor"),
)
print("Evaluation of the Product Model and the Tweedie Regressor on target PurePremium")
with pd.option_context("display.expand_frame_repr", False):
print(scores)
Evaluation of the Product Model and the Tweedie Regressor on target PurePremium
Product Model TweedieRegressor
subset train test train test
metric
D² explained NaN NaN 1.640000e-02 1.370000e-02
mean Tweedie dev p=1.5000 7.669930e+01 7.617050e+01 7.640770e+01 7.640880e+01
mean Tweedie dev p=1.7000 3.695740e+01 3.683980e+01 3.682880e+01 3.692270e+01
mean Tweedie dev p=1.8000 3.046010e+01 3.040530e+01 3.037600e+01 3.045390e+01
mean Tweedie dev p=1.9000 3.387580e+01 3.385000e+01 3.382120e+01 3.387830e+01
mean Tweedie dev p=1.9900 2.015716e+02 2.015414e+02 2.015347e+02 2.015587e+02
mean Tweedie dev p=1.9990 1.914573e+03 1.914370e+03 1.914538e+03 1.914387e+03
mean Tweedie dev p=1.9999 1.904751e+04 1.904556e+04 1.904747e+04 1.904558e+04
mean abs. error 2.730119e+02 2.722128e+02 2.739865e+02 2.731249e+02
mean squared error 3.295040e+07 3.212197e+07 3.295505e+07 3.213056e+07
在这个例子中,两种建模方法都产生了相当的性能指标。由于实现原因,乘积模型的解释方差百分比 \(D^2\) 不可用。
我们还可以通过比较测试和训练子集上的观察到的和预测的总索赔金额来验证这些模型。我们发现,平均而言,这两种模型都倾向于低估总索赔金额(但这种行为取决于正则化的程度)。
res = []
for subset_label, X, df in [
("train", X_train, df_train),
("test", X_test, df_test),
]:
exposure = df["Exposure"].values
res.append(
{
"subset": subset_label,
"observed": df["ClaimAmount"].values.sum(),
"predicted, frequency*severity model": np.sum(
exposure * glm_freq.predict(X) * glm_sev.predict(X)
),
"predicted, tweedie, power=%.2f"
% glm_pure_premium.power: np.sum(exposure * glm_pure_premium.predict(X)),
}
)
print(pd.DataFrame(res).set_index("subset").T)
subset train test
observed 3.917618e+07 1.299546e+07
predicted, frequency*severity model 3.916555e+07 1.313276e+07
predicted, tweedie, power=1.90 3.951751e+07 1.325198e+07
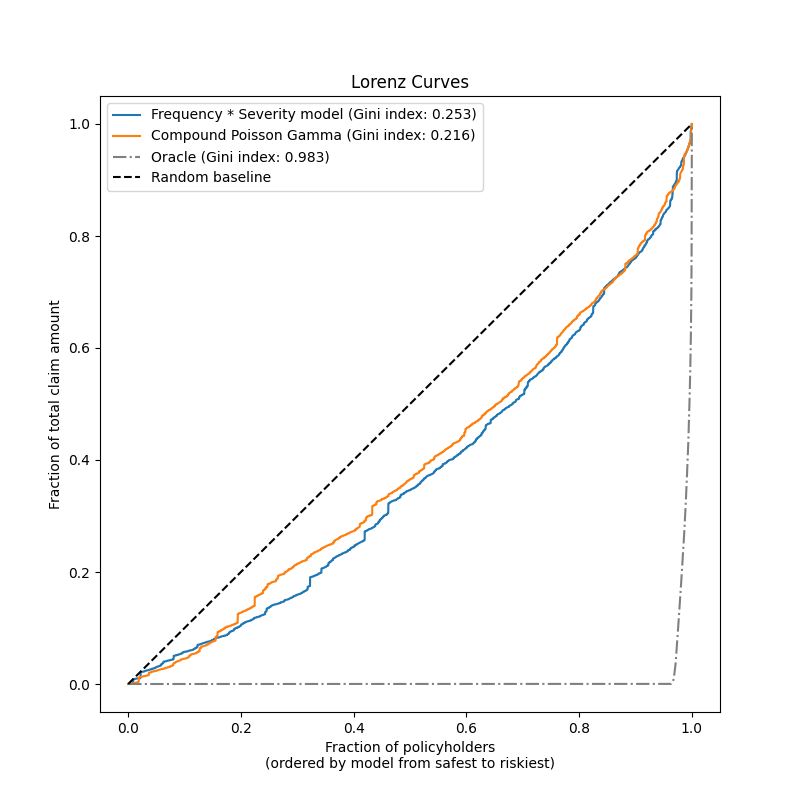
最后,我们可以通过累积索赔的图表来比较这两个模型:对于每个模型,根据模型预测将保单持有人从最安全到最危险进行排序,并在 y 轴上绘制观察到的总累积索赔的比例。这个图通常被称为模型的有序洛伦兹曲线。
基尼系数(基于曲线与对角线之间的面积)可以用作模型选择指标,以量化模型对保单持有人进行排序的能力。请注意,该指标并不反映模型在总赔付金额绝对值方面的准确预测能力,而仅在相对金额方面作为排序指标。基尼系数的上限为1.0,但即使是按观察到的赔付金额对保单持有人进行排序的理想模型也无法达到1.0的得分。
我们观察到,尽管由于从少量特征进行预测的自然难度,大多数事故是不可预测的,并且可能由模型输入特征完全未描述的环境因素引起,但这两种模型在按风险程度对保单持有人进行排序方面都显著优于随机。然而,它们都远不及理想模型。
请注意,Gini指数仅描述模型的排序性能,而不描述其校准情况:对预测值进行任何单调变换都不会改变模型的Gini指数。
最后需要强调的是,直接在纯保费上拟合的复合泊松伽马模型在操作上更简单开发和维护,因为它只包含一个scikit-learn估计器,而不是一对模型,每个模型都有自己的一组超参数。
from sklearn.metrics import auc
def lorenz_curve(y_true, y_pred, exposure):
y_true, y_pred = np.asarray(y_true), np.asarray(y_pred)
exposure = np.asarray(exposure)
# 按预测风险从低到高排序样本:
ranking = np.argsort(y_pred)
ranked_exposure = exposure[ranking]
ranked_pure_premium = y_true[ranking]
cumulated_claim_amount = np.cumsum(ranked_pure_premium * ranked_exposure)
cumulated_claim_amount /= cumulated_claim_amount[-1]
cumulated_samples = np.linspace(0, 1, len(cumulated_claim_amount))
return cumulated_samples, cumulated_claim_amount
fig, ax = plt.subplots(figsize=(8, 8))
y_pred_product = glm_freq.predict(X_test) * glm_sev.predict(X_test)
y_pred_total = glm_pure_premium.predict(X_test)
for label, y_pred in [
("Frequency * Severity model", y_pred_product),
("Compound Poisson Gamma", y_pred_total),
]:
ordered_samples, cum_claims = lorenz_curve(
df_test["PurePremium"], y_pred, df_test["Exposure"]
)
gini = 1 - 2 * auc(ordered_samples, cum_claims)
label += " (Gini index: {:.3f})".format(gini)
ax.plot(ordered_samples, cum_claims, linestyle="-", label=label)
# Oracle model: y_pred == y_test
ordered_samples, cum_claims = lorenz_curve(
df_test["PurePremium"], df_test["PurePremium"], df_test["Exposure"]
)
gini = 1 - 2 * auc(ordered_samples, cum_claims)
label = "Oracle (Gini index: {:.3f})".format(gini)
ax.plot(ordered_samples, cum_claims, linestyle="-.", color="gray", label=label)
# 随机基线
ax.plot([0, 1], [0, 1], linestyle="--", color="black", label="Random baseline")
ax.set(
title="Lorenz Curves",
xlabel="Fraction of policyholders\n(ordered by model from safest to riskiest)",
ylabel="Fraction of total claim amount",
)
ax.legend(loc="upper left")
plt.plot()
[]
Total running time of the script: (0 minutes 5.230 seconds)
Related examples