Note

Go to the end to download the full example code. or to run this example in your browser via Binder

人脸数据集分解#

本示例将 The Olivetti faces dataset 应用于来自模块 sklearn.decomposition 的不同无监督矩阵分解（降维）方法（参见文档章节信号分解为成分（矩阵分解问题））。

作者: Vlad Niculae, Alexandre Gramfort
许可证: BSD 3 条款

数据集准备#

加载和预处理 Olivetti 人脸数据集。

import logging

import matplotlib.pyplot as plt
from numpy.random import RandomState

from sklearn import cluster, decomposition
from sklearn.datasets import fetch_olivetti_faces

rng = RandomState(0)

# 在标准输出上显示进度日志
logging.basicConfig(level=logging.INFO, format="%(asctime)s %(levelname)s %(message)s")

faces, _ = fetch_olivetti_faces(return_X_y=True, shuffle=True, random_state=rng)
n_samples, n_features = faces.shape

# 全局中心化（聚焦于一个特征，对所有样本进行中心化）
faces_centered = faces - faces.mean(axis=0)

# 局部中心化（聚焦于一个样本，对所有特征进行中心化）
faces_centered -= faces_centered.mean(axis=1).reshape(n_samples, -1)

print("Dataset consists of %d faces" % n_samples)

Dataset consists of 400 faces

定义一个基础函数来绘制人脸画廊。

n_row, n_col = 2, 3
n_components = n_row * n_col
image_shape = (64, 64)


def plot_gallery(title, images, n_col=n_col, n_row=n_row, cmap=plt.cm.gray):
    fig, axs = plt.subplots(
        nrows=n_row,
        ncols=n_col,
        figsize=(2.0 * n_col, 2.3 * n_row),
        facecolor="white",
        constrained_layout=True,
    )
    fig.set_constrained_layout_pads(w_pad=0.01, h_pad=0.02, hspace=0, wspace=0)
    fig.set_edgecolor("black")
    fig.suptitle(title, size=16)
    for ax, vec in zip(axs.flat, images):
        vmax = max(vec.max(), -vec.min())
        im = ax.imshow(
            vec.reshape(image_shape),
            cmap=cmap,
            interpolation="nearest",
            vmin=-vmax,
            vmax=vmax,
        )
        ax.axis("off")

    fig.colorbar(im, ax=axs, orientation="horizontal", shrink=0.99, aspect=40, pad=0.01)
    plt.show()

让我们来看一下我们的数据。灰色表示负值，白色表示正值。

plot_gallery("Faces from dataset", faces_centered[:n_components])

分解#

初始化不同的分解估计器，并将它们拟合到所有图像上，然后绘制一些结果。每个估计器提取6个分量作为向量 \(h \in \mathbb{R}^{4096}\) 。我们只是将这些向量以64x64像素图像的形式进行人性化的可视化展示。

请参阅用户指南了解更多信息。

Eigenfaces - 使用随机SVD的PCA#

使用数据的奇异值分解（SVD）进行线性降维，将其投影到低维空间。

通过 sklearn.decomposition.PCA 的 Eigenfaces 估计器还提供了一个标量 noise_variance_ （像素方差的均值），该标量无法显示为图像。

pca_estimator = decomposition.PCA(
    n_components=n_components, svd_solver="randomized", whiten=True
)
pca_estimator.fit(faces_centered)
plot_gallery(
    "Eigenfaces - PCA using randomized SVD", pca_estimator.components_[:n_components]
)

非负分解组件 - NMF#

估计非负原始数据为两个非负矩阵的乘积。

nmf_estimator = decomposition.NMF(n_components=n_components, tol=5e-3)
nmf_estimator.fit(faces)  # original non- negative dataset
plot_gallery("Non-negative components - NMF", nmf_estimator.components_[:n_components])

独立成分 - FastICA#

独立成分分析将多变量向量分解为相加的子成分，这些子成分是最大程度独立的。

ica_estimator = decomposition.FastICA(
    n_components=n_components, max_iter=400, whiten="arbitrary-variance", tol=15e-5
)
ica_estimator.fit(faces_centered)
plot_gallery(
    "Independent components - FastICA", ica_estimator.components_[:n_components]
)

稀疏成分 - MiniBatchSparsePCA#

小批量稀疏PCA（MiniBatchSparsePCA ）提取最能重构数据的稀疏成分集。这个变体比类似的 SparsePCA 更快，但准确性较低。

batch_pca_estimator = decomposition.MiniBatchSparsePCA(
    n_components=n_components, alpha=0.1, max_iter=100, batch_size=3, random_state=rng
)
batch_pca_estimator.fit(faces_centered)
plot_gallery(
    "Sparse components - MiniBatchSparsePCA",
    batch_pca_estimator.components_[:n_components],
)

字典学习#

默认情况下，MiniBatchDictionaryLearning 将数据分成小批量，并通过对小批量进行循环以指定的迭代次数在线优化。

batch_dict_estimator = decomposition.MiniBatchDictionaryLearning(
    n_components=n_components, alpha=0.1, max_iter=50, batch_size=3, random_state=rng
)
batch_dict_estimator.fit(faces_centered)
plot_gallery("Dictionary learning", batch_dict_estimator.components_[:n_components])

聚类中心 - MiniBatchKMeans#

sklearn.cluster.MiniBatchKMeans 计算效率高，并通过 partial_fit 方法实现在线学习。因此，将一些耗时的算法与 MiniBatchKMeans 结合起来可能会有益处。

kmeans_estimator = cluster.MiniBatchKMeans(
    n_clusters=n_components,
    tol=1e-3,
    batch_size=20,
    max_iter=50,
    random_state=rng,
)
kmeans_estimator.fit(faces_centered)
plot_gallery(
    "Cluster centers - MiniBatchKMeans",
    kmeans_estimator.cluster_centers_[:n_components],
)

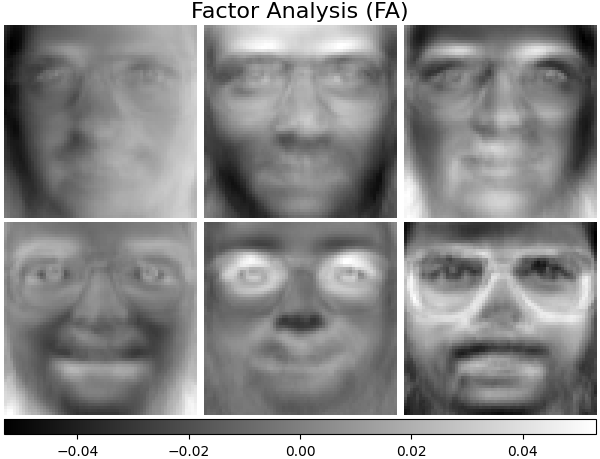
因子分析成分 - FA#

FactorAnalysis 类似于 PCA ，但具有独立建模输入空间每个方向方差（异方差噪声）的优势。更多内容请参阅用户指南。

fa_estimator = decomposition.FactorAnalysis(n_components=n_components, max_iter=20)
fa_estimator.fit(faces_centered)
plot_gallery("Factor Analysis (FA)", fa_estimator.components_[:n_components])

# --- 像素级方差
plt.figure(figsize=(3.2, 3.6), facecolor="white", tight_layout=True)
vec = fa_estimator.noise_variance_
vmax = max(vec.max(), -vec.min())
plt.imshow(
    vec.reshape(image_shape),
    cmap=plt.cm.gray,
    interpolation="nearest",
    vmin=-vmax,
    vmax=vmax,
)
plt.axis("off")
plt.title("Pixelwise variance from \n Factor Analysis (FA)", size=16, wrap=True)
plt.colorbar(orientation="horizontal", shrink=0.8, pad=0.03)
plt.show()

分解：字典学习#

在接下来的部分中，让我们更详细地考虑 DictionaryLearning 。字典学习是一个问题，其目的是找到输入数据的稀疏表示，作为简单元素的组合。这些简单元素构成了一个字典。可以约束字典和/或编码系数为正，以匹配数据中可能存在的约束。

MiniBatchDictionaryLearning 实现了一种更快但精度较低的字典学习算法版本，更适合处理大型数据集。请在用户指南中阅读更多内容。

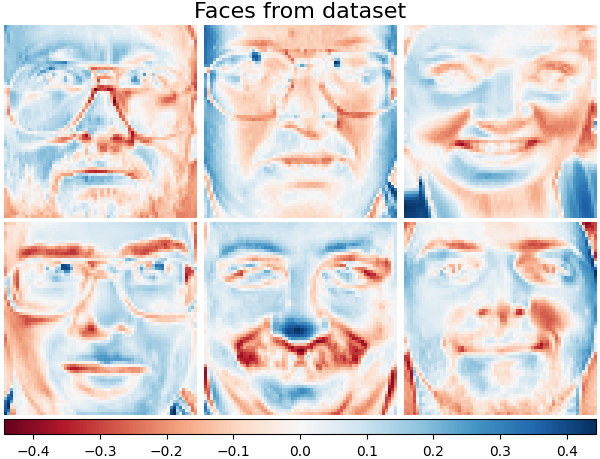
绘制数据集中相同的样本，但使用另一种颜色映射。红色表示负值，蓝色表示正值，白色表示零。

plot_gallery("Faces from dataset", faces_centered[:n_components], cmap=plt.cm.RdBu)

类似于之前的示例，我们更改参数并在所有图像上训练 MiniBatchDictionaryLearning 估计器。通常，字典学习和稀疏编码将输入数据分解为字典和编码系数矩阵。\(X \approx UV\) ，其中 \(X = [x_1, . . . , x_n]\) ，\(X \in \mathbb{R}^{m×n}\) ，字典 \(U \in \mathbb{R}^{m×k}\) ，编码系数 \(V \in \mathbb{R}^{k×n}\) 。

此外，以下是字典和编码系数受到正约束时的结果。

字典学习 - 正字典#

在以下部分中，我们在寻找字典时强制执行正值。

dict_pos_dict_estimator = decomposition.MiniBatchDictionaryLearning(
    n_components=n_components,
    alpha=0.1,
    max_iter=50,
    batch_size=3,
    random_state=rng,
    positive_dict=True,
)
dict_pos_dict_estimator.fit(faces_centered)
plot_gallery(
    "Dictionary learning - positive dictionary",
    dict_pos_dict_estimator.components_[:n_components],
    cmap=plt.cm.RdBu,
)

Dictionary learning - positive dictionary

字典学习 - 正码

下面我们将编码系数限制为一个正矩阵。

dict_pos_code_estimator = decomposition.MiniBatchDictionaryLearning(
    n_components=n_components,
    alpha=0.1,
    max_iter=50,
    batch_size=3,
    fit_algorithm="cd",
    random_state=rng,
    positive_code=True,
)
dict_pos_code_estimator.fit(faces_centered)
plot_gallery(
    "Dictionary learning - positive code",
    dict_pos_code_estimator.components_[:n_components],
    cmap=plt.cm.RdBu,
)

字典学习 - 正字典和编码

另外，如果字典值和编码系数受到正约束，结果如下。

dict_pos_estimator = decomposition.MiniBatchDictionaryLearning(
    n_components=n_components,
    alpha=0.1,
    max_iter=50,
    batch_size=3,
    fit_algorithm="cd",
    random_state=rng,
    positive_dict=True,
    positive_code=True,
)
dict_pos_estimator.fit(faces_centered)
plot_gallery(
    "Dictionary learning - positive dictionary & code",
    dict_pos_estimator.components_[:n_components],
    cmap=plt.cm.RdBu,
)