Note
Go to the end to download the full example code. or to run this example in your browser via Binder
在构建估计器之前填补缺失值#
可以使用基础的 SimpleImputer 通过均值、中位数或最频繁值来替换缺失值。
在这个示例中,我们将研究不同的填补技术:
用常数值 0 填补
用每个特征的均值填补,并结合缺失指示辅助变量
k 近邻填补
迭代填补
我们将使用两个数据集:糖尿病数据集,该数据集由从糖尿病患者收集的 10 个特征变量组成,旨在预测疾病进展;以及加州房价数据集,其目标是加州各区的房价中位数。
由于这两个数据集都没有缺失值,我们将删除一些值以创建具有人为缺失数据的新版本。然后将 RandomForestRegressor 在完整原始数据集上的性能与在使用不同技术填补了人为缺失值的修改数据集上的性能进行比较。
# 作者:scikit-learn 开发者
# SPDX-License-Identifier: BSD-3-Clause
下载数据并生成缺失值集合
首先,我们下载两个数据集。Diabetes 数据集随 scikit-learn 一起提供。它有 442 条目,每条有 10 个特征。California Housing 数据集要大得多,有 20640 条目和 8 个特征。它需要下载。为了加快计算速度,我们只使用前 400 条目,但您可以随意使用整个数据集。
import numpy as np
from sklearn.datasets import fetch_california_housing, load_diabetes
rng = np.random.RandomState(42)
X_diabetes, y_diabetes = load_diabetes(return_X_y=True)
X_california, y_california = fetch_california_housing(return_X_y=True)
X_california = X_california[:300]
y_california = y_california[:300]
X_diabetes = X_diabetes[:300]
y_diabetes = y_diabetes[:300]
def add_missing_values(X_full, y_full):
n_samples, n_features = X_full.shape
# 在75%的行中添加缺失值
missing_rate = 0.75
n_missing_samples = int(n_samples * missing_rate)
missing_samples = np.zeros(n_samples, dtype=bool)
missing_samples[:n_missing_samples] = True
rng.shuffle(missing_samples)
missing_features = rng.randint(0, n_features, n_missing_samples)
X_missing = X_full.copy()
X_missing[missing_samples, missing_features] = np.nan
y_missing = y_full.copy()
return X_missing, y_missing
X_miss_california, y_miss_california = add_missing_values(X_california, y_california)
X_miss_diabetes, y_miss_diabetes = add_missing_values(X_diabetes, y_diabetes)
填补缺失数据并评分
现在我们将编写一个函数,对不同填补方法处理后的数据进行评分。让我们分别查看每个填补方法:
rng = np.random.RandomState(0)
from sklearn.ensemble import RandomForestRegressor
# 要使用实验性的IterativeImputer,我们需要明确地请求它:
from sklearn.experimental import enable_iterative_imputer # noqa
from sklearn.impute import IterativeImputer, KNNImputer, SimpleImputer
from sklearn.model_selection import cross_val_score
from sklearn.pipeline import make_pipeline
N_SPLITS = 4
regressor = RandomForestRegressor(random_state=0)
缺失信息#
除了填补缺失值之外,插补器还具有一个 add_indicator 参数,该参数标记缺失的值,这些值可能包含一些信息。
def get_scores_for_imputer(imputer, X_missing, y_missing):
estimator = make_pipeline(imputer, regressor)
impute_scores = cross_val_score(
estimator, X_missing, y_missing, scoring="neg_mean_squared_error", cv=N_SPLITS
)
return impute_scores
x_labels = []
mses_california = np.zeros(5)
stds_california = np.zeros(5)
mses_diabetes = np.zeros(5)
stds_diabetes = np.zeros(5)
估算分数#
首先,我们想要估算原始数据的分数:
def get_full_score(X_full, y_full):
full_scores = cross_val_score(
regressor, X_full, y_full, scoring="neg_mean_squared_error", cv=N_SPLITS
)
return full_scores.mean(), full_scores.std()
mses_california[0], stds_california[0] = get_full_score(X_california, y_california)
mses_diabetes[0], stds_diabetes[0] = get_full_score(X_diabetes, y_diabetes)
x_labels.append("Full data")
将缺失值替换为0#
现在我们将估算在缺失值被替换为0的数据上的得分:
def get_impute_zero_score(X_missing, y_missing):
imputer = SimpleImputer(
missing_values=np.nan, add_indicator=True, strategy="constant", fill_value=0
)
zero_impute_scores = get_scores_for_imputer(imputer, X_missing, y_missing)
return zero_impute_scores.mean(), zero_impute_scores.std()
mses_california[1], stds_california[1] = get_impute_zero_score(
X_miss_california, y_miss_california
)
mses_diabetes[1], stds_diabetes[1] = get_impute_zero_score(
X_miss_diabetes, y_miss_diabetes
)
x_labels.append("Zero imputation")
kNN 插补缺失值#
KNNImputer 使用所需数量的最近邻的加权或非加权平均值来填补缺失值。
def get_impute_knn_score(X_missing, y_missing):
imputer = KNNImputer(missing_values=np.nan, add_indicator=True)
knn_impute_scores = get_scores_for_imputer(imputer, X_missing, y_missing)
return knn_impute_scores.mean(), knn_impute_scores.std()
mses_california[2], stds_california[2] = get_impute_knn_score(
X_miss_california, y_miss_california
)
mses_diabetes[2], stds_diabetes[2] = get_impute_knn_score(
X_miss_diabetes, y_miss_diabetes
)
x_labels.append("KNN Imputation")
用均值填补缺失值#
def get_impute_mean(X_missing, y_missing):
imputer = SimpleImputer(missing_values=np.nan, strategy="mean", add_indicator=True)
mean_impute_scores = get_scores_for_imputer(imputer, X_missing, y_missing)
return mean_impute_scores.mean(), mean_impute_scores.std()
mses_california[3], stds_california[3] = get_impute_mean(
X_miss_california, y_miss_california
)
mses_diabetes[3], stds_diabetes[3] = get_impute_mean(X_miss_diabetes, y_miss_diabetes)
x_labels.append("Mean Imputation")
迭代插补缺失值#
另一种选择是 IterativeImputer 。它使用循环线性回归,将每个具有缺失值的特征依次建模为其他特征的函数。
实现的版本假设输出变量为高斯分布。如果你的特征显然不是正态分布,考虑将它们转换为更接近正态分布,以可能提高性能。
def get_impute_iterative(X_missing, y_missing):
imputer = IterativeImputer(
missing_values=np.nan,
add_indicator=True,
random_state=0,
n_nearest_features=3,
max_iter=1,
sample_posterior=True,
)
iterative_impute_scores = get_scores_for_imputer(imputer, X_missing, y_missing)
return iterative_impute_scores.mean(), iterative_impute_scores.std()
mses_california[4], stds_california[4] = get_impute_iterative(
X_miss_california, y_miss_california
)
mses_diabetes[4], stds_diabetes[4] = get_impute_iterative(
X_miss_diabetes, y_miss_diabetes
)
x_labels.append("Iterative Imputation")
mses_diabetes = mses_diabetes * -1
mses_california = mses_california * -1
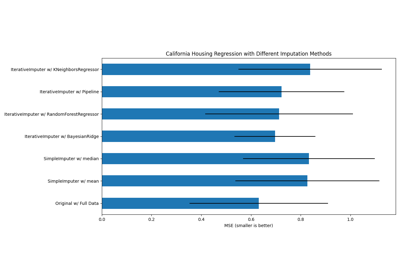
绘制结果
最后我们将可视化分数:
import matplotlib.pyplot as plt
n_bars = len(mses_diabetes)
xval = np.arange(n_bars)
colors = ["r", "g", "b", "orange", "black"]
# 绘制糖尿病结果
plt.figure(figsize=(12, 6))
ax1 = plt.subplot(121)
for j in xval:
ax1.barh(
j,
mses_diabetes[j],
xerr=stds_diabetes[j],
color=colors[j],
alpha=0.6,
align="center",
)
ax1.set_title("Imputation Techniques with Diabetes Data")
ax1.set_xlim(left=np.min(mses_diabetes) * 0.9, right=np.max(mses_diabetes) * 1.1)
ax1.set_yticks(xval)
ax1.set_xlabel("MSE")
ax1.invert_yaxis()
ax1.set_yticklabels(x_labels)
# 绘制加利福尼亚数据集结果
ax2 = plt.subplot(122)
for j in xval:
ax2.barh(
j,
mses_california[j],
xerr=stds_california[j],
color=colors[j],
alpha=0.6,
align="center",
)
ax2.set_title("Imputation Techniques with California Data")
ax2.set_yticks(xval)
ax2.set_xlabel("MSE")
ax2.invert_yaxis()
ax2.set_yticklabels([""] * n_bars)
plt.show()
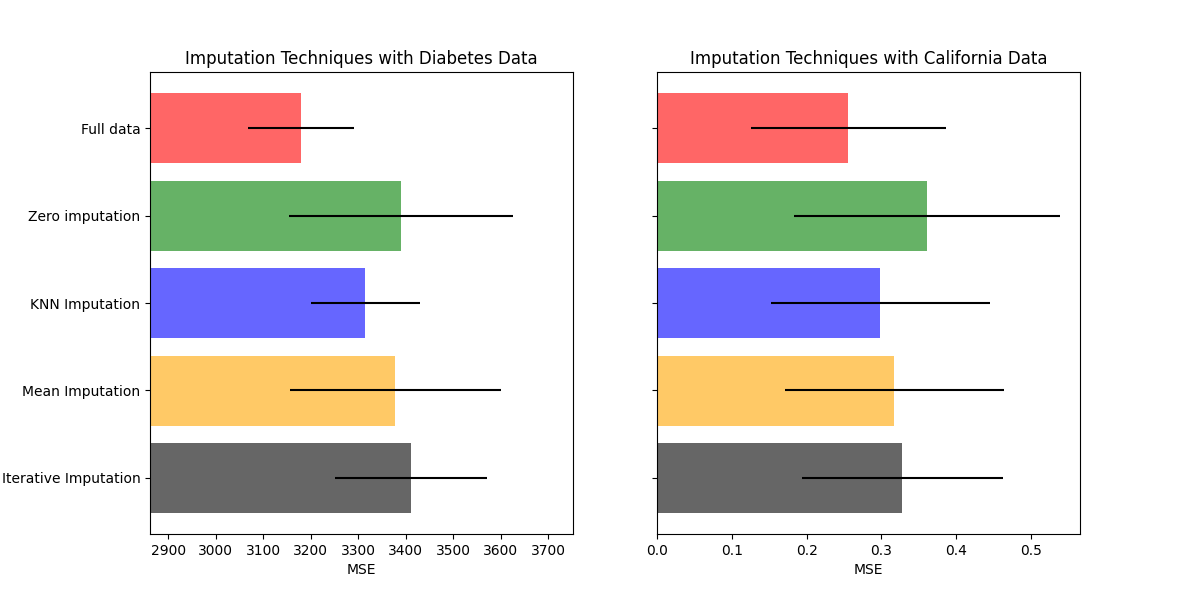
你也可以尝试不同的技术。例如,中位数对于具有高幅度变量的数据来说是一个更稳健的估计量,这些高幅度变量可能会主导结果(也称为“长尾”)。
Total running time of the script: (0 minutes 11.203 seconds)
Related examples