Note

Go to the end to download the full example code. or to run this example in your browser via Binder

真实数据集上的异常值检测#

本示例说明了在真实数据集上进行稳健协方差估计的必要性。这对于异常值检测和更好地理解数据结构都很有用。

我们从葡萄酒数据集中选择了两组两个变量，作为使用多种异常值检测工具进行分析的示例。为了便于可视化，我们使用了二维示例，但需要注意的是，在高维情况下，事情并不那么简单，这一点将在后文中指出。

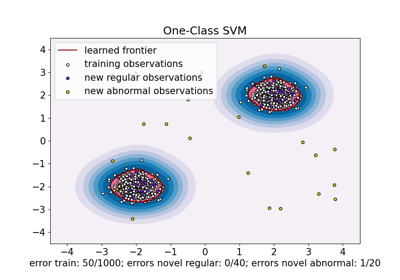
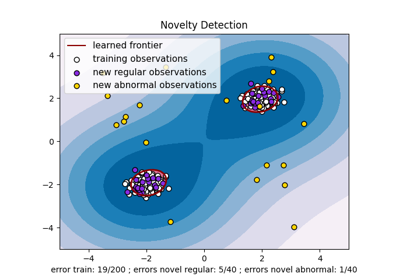
在下面的两个示例中，主要结果是经验协方差估计作为一种非稳健方法，受观测值的异质结构影响很大。尽管稳健协方差估计能够聚焦于数据分布的主要模式，但它坚持认为数据应服从高斯分布，从而导致对数据结构的某些偏差估计，但在某种程度上仍然是准确的。一类支持向量机（One-Class SVM）不假设数据分布的任何参数形式，因此可以更好地建模数据的复杂形状。

# 作者：scikit-learn 开发者
# SPDX-License-Identifier：BSD-3-Clause

第一个例子#

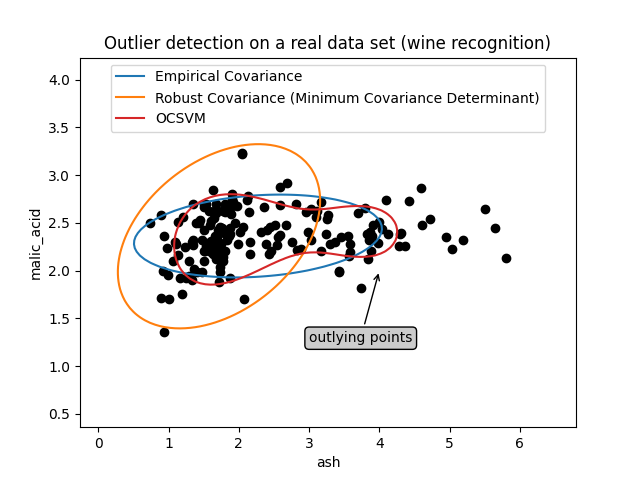
第一个示例说明了当存在离群点时，最小协方差行列式稳健估计器如何帮助集中于相关簇。在这里，经验协方差估计被主簇之外的点所偏斜。当然，一些筛选工具会指出存在两个簇（支持向量机、高斯混合模型、单变量离群点检测等）。但如果这是一个高维示例，这些方法都不容易应用。

from sklearn.covariance import EllipticEnvelope
from sklearn.inspection import DecisionBoundaryDisplay
from sklearn.svm import OneClassSVM

estimators = {
    "Empirical Covariance": EllipticEnvelope(support_fraction=1.0, contamination=0.25),
    "Robust Covariance (Minimum Covariance Determinant)": EllipticEnvelope(
        contamination=0.25
    ),
    "OCSVM": OneClassSVM(nu=0.25, gamma=0.35),
}

import matplotlib.lines as mlines
import matplotlib.pyplot as plt

from sklearn.datasets import load_wine

X = load_wine()["data"][:, [1, 2]]  # two clusters

fig, ax = plt.subplots()
colors = ["tab:blue", "tab:orange", "tab:red"]
# 学习一个用于异常检测的前沿方法，结合多个分类器
legend_lines = []
for color, (name, estimator) in zip(colors, estimators.items()):
    estimator.fit(X)
    DecisionBoundaryDisplay.from_estimator(
        estimator,
        X,
        response_method="decision_function",
        plot_method="contour",
        levels=[0],
        colors=color,
        ax=ax,
    )
    legend_lines.append(mlines.Line2D([], [], color=color, label=name))


ax.scatter(X[:, 0], X[:, 1], color="black")
bbox_args = dict(boxstyle="round", fc="0.8")
arrow_args = dict(arrowstyle="->")
ax.annotate(
    "outlying points",
    xy=(4, 2),
    xycoords="data",
    textcoords="data",
    xytext=(3, 1.25),
    bbox=bbox_args,
    arrowprops=arrow_args,
)
ax.legend(handles=legend_lines, loc="upper center")
_ = ax.set(
    xlabel="ash",
    ylabel="malic_acid",
    title="Outlier detection on a real data set (wine recognition)",
)

Outlier detection on a real data set (wine recognition)

第二个例子#

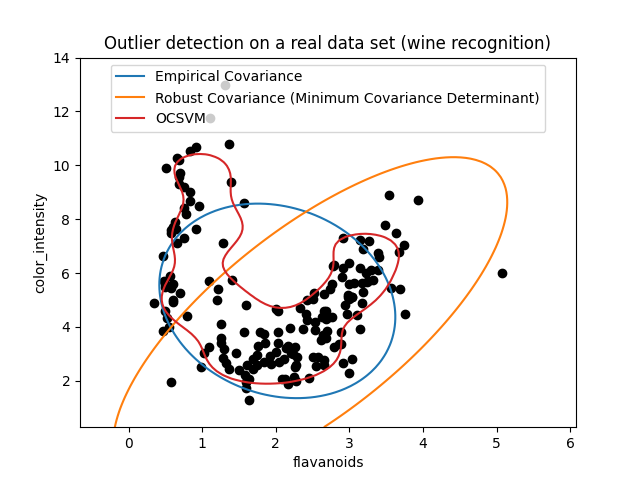
第二个示例展示了最小协方差行列式（Minimum Covariance Determinant）稳健协方差估计器集中于数据分布主要模式的能力：尽管由于香蕉形分布，协方差难以估计，但位置似乎被很好地估计了。不管怎样，我们可以去除一些离群观测值。单类支持向量机（One-Class SVM）能够捕捉真实的数据结构，但难点在于调整其核带宽参数，以在数据散布矩阵的形状和数据过拟合风险之间取得良好的平衡。

X = load_wine()["data"][:, [6, 9]]  # "banana"-shaped

fig, ax = plt.subplots()
colors = ["tab:blue", "tab:orange", "tab:red"]
# 学习一个用于异常检测的前沿方法，结合多个分类器
legend_lines = []
for color, (name, estimator) in zip(colors, estimators.items()):
    estimator.fit(X)
    DecisionBoundaryDisplay.from_estimator(
        estimator,
        X,
        response_method="decision_function",
        plot_method="contour",
        levels=[0],
        colors=color,
        ax=ax,
    )
    legend_lines.append(mlines.Line2D([], [], color=color, label=name))


ax.scatter(X[:, 0], X[:, 1], color="black")
ax.legend(handles=legend_lines, loc="upper center")
ax.set(
    xlabel="flavanoids",
    ylabel="color_intensity",
    title="Outlier detection on a real data set (wine recognition)",
)

plt.show()