Note

Go to the end to download the full example code. or to run this example in your browser via Binder

多项式和样条插值#

本示例演示了如何使用岭回归通过多项式（最高到 degree 次）来逼近一个函数。我们展示了在给定 n_samples 个一维点 x_i 的情况下的两种不同方法：

PolynomialFeatures 生成所有最高到 degree 次的单项式。这给我们提供了所谓的范德蒙德矩阵，该矩阵有 n_samples 行和 degree + 1 列：

[[1, x_0, x_0 ** 2, x_0 ** 3, …, x_0 ** degree],
[1, x_1, x_1 ** 2, x_1 ** 3, …, x_1 ** degree], …]

直观地，这个矩阵可以被解释为一个伪特征矩阵（点的幂次）。该矩阵类似于（但不同于）由多项式核引起的矩阵。
SplineTransformer 生成B样条基函数。B样条的基函数是一个分段多项式函数，其次数为 degree ，且仅在 degree+1 个连续节点之间非零。给定 n_knots 个节点，这将产生一个 n_samples 行和 n_knots + degree - 1 列的矩阵：

[[basis_1(x_0), basis_2(x_0), …],
[basis_1(x_1), basis_2(x_1), …], …]

本示例表明，这两个转换器非常适合使用线性模型来建模非线性效应，使用管道来添加非线性特征。核方法扩展了这一思想，可以引入非常高（甚至无限）维的特征空间。

# 作者：scikit-learn 开发者
# SPDX-License-Identifier: BSD-3-Clause

import matplotlib.pyplot as plt
import numpy as np

from sklearn.linear_model import Ridge
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import PolynomialFeatures, SplineTransformer

我们首先定义一个我们打算近似的函数，并准备绘制它。

def f(x):
    """通过多项式插值来逼近的函数。"""
    return x * np.sin(x)


# 我们想要绘制的整个范围
x_plot = np.linspace(-1, 11, 100)

为了增加趣味性，我们只提供一小部分点进行训练。

x_train = np.linspace(0, 10, 100)
rng = np.random.RandomState(0)
x_train = np.sort(rng.choice(x_train, size=20, replace=False))
y_train = f(x_train)

# 创建这些数组的二维数组版本以供转换器使用
X_train = x_train[:, np.newaxis]
X_plot = x_plot[:, np.newaxis]

现在我们已经准备好创建多项式特征和样条，拟合训练点并展示它们的插值效果。

# 绘图函数
lw = 2
fig, ax = plt.subplots()
ax.set_prop_cycle(
    color=["black", "teal", "yellowgreen", "gold", "darkorange", "tomato"]
)
ax.plot(x_plot, f(x_plot), linewidth=lw, label="ground truth")

# plot training points
ax.scatter(x_train, y_train, label="training points")

# 多项式特征
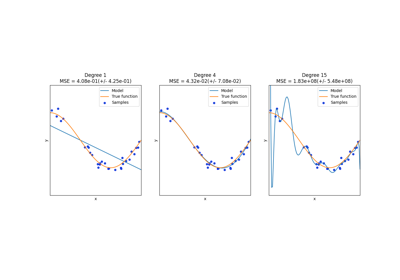
for degree in [3, 4, 5]:
    model = make_pipeline(PolynomialFeatures(degree), Ridge(alpha=1e-3))
    model.fit(X_train, y_train)
    y_plot = model.predict(X_plot)
    ax.plot(x_plot, y_plot, label=f"degree {degree}")

# B样条具有4 + 3 - 1 = 6个基函数
model = make_pipeline(SplineTransformer(n_knots=4, degree=3), Ridge(alpha=1e-3))
model.fit(X_train, y_train)

y_plot = model.predict(X_plot)
ax.plot(x_plot, y_plot, label="B-spline")
ax.legend(loc="lower center")
ax.set_ylim(-20, 10)
plt.show()

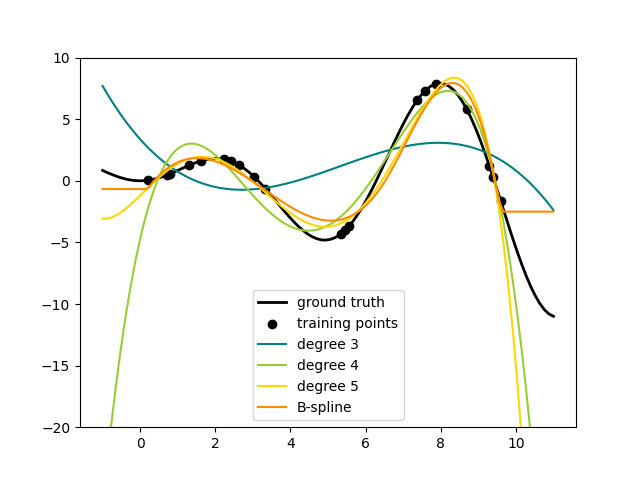
这很好地表明了高次多项式可以更好地拟合数据。但同时，过高的幂次可能会表现出不必要的振荡行为，并且在拟合数据范围之外进行外推时尤其危险。这是B样条的一个优势。它们通常可以像多项式一样很好地拟合数据，并表现出非常平滑的行为。它们在控制外推方面也有很好的选项，默认情况下会继续保持常数。请注意，大多数情况下，你宁愿增加节点的数量，但保持 degree=3 。

为了更深入地了解生成的特征基，我们分别绘制了两个转换器的所有列。

fig, axes = plt.subplots(ncols=2, figsize=(16, 5))
pft = PolynomialFeatures(degree=3).fit(X_train)
axes[0].plot(x_plot, pft.transform(X_plot))
axes[0].legend(axes[0].lines, [f"degree {n}" for n in range(4)])
axes[0].set_title("PolynomialFeatures")

splt = SplineTransformer(n_knots=4, degree=3).fit(X_train)
axes[1].plot(x_plot, splt.transform(X_plot))
axes[1].legend(axes[1].lines, [f"spline {n}" for n in range(6)])
axes[1].set_title("SplineTransformer")

# 绘制样条的节点
knots = splt.bsplines_[0].t
axes[1].vlines(knots[3:-3], ymin=0, ymax=0.8, linestyles="dashed")
plt.show()

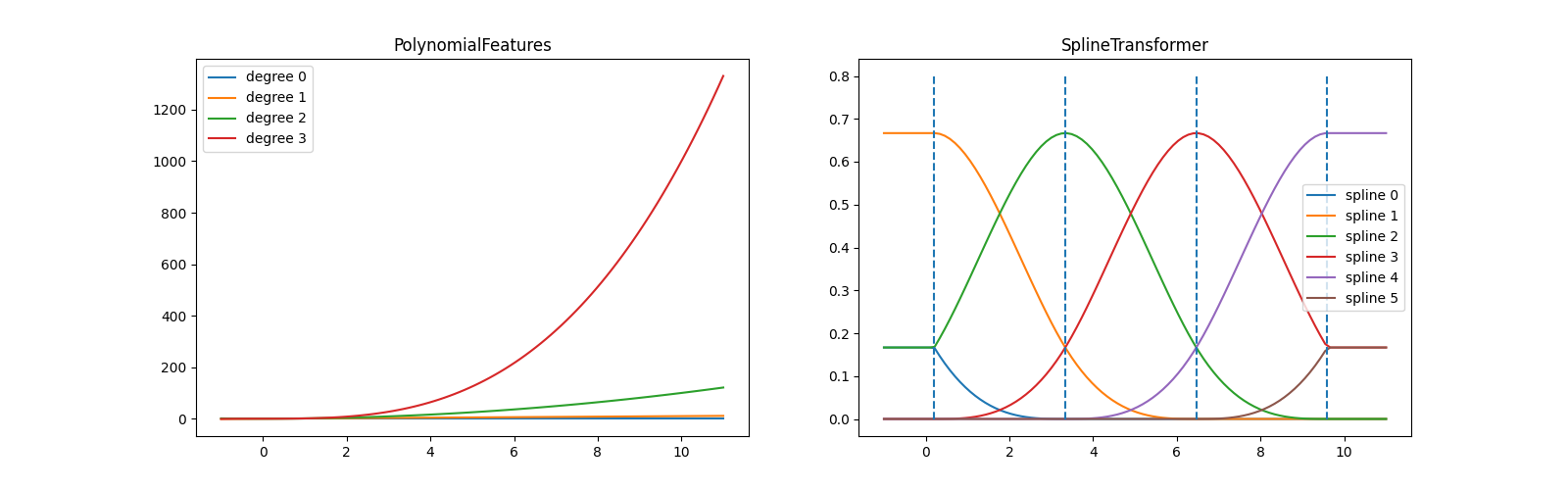
在左图中，我们可以识别出从 x**0 到 x**3 的简单单项式对应的曲线。在右图中，我们可以看到六个三次B样条基函数以及在 fit 过程中选择的四个节点位置。请注意，在拟合区间的左右两侧各有 degree 个额外的节点。这些节点出于技术原因存在，因此我们不展示它们。每个基函数都有局部支撑，并在拟合范围之外继续作为常数。这种外推行为可以通过参数 extrapolation 来改变。

周期样条#

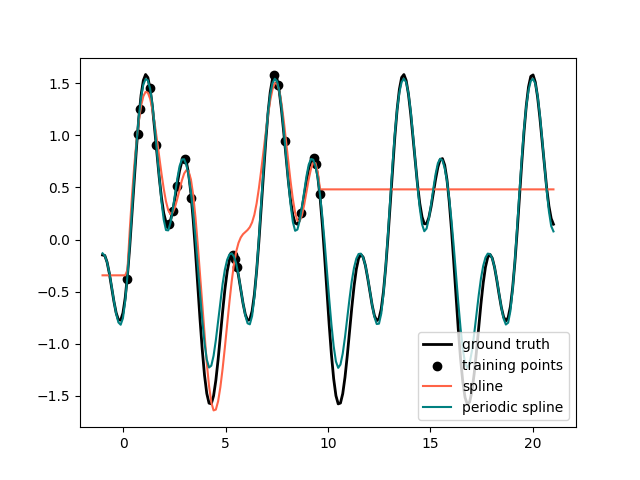
在前面的例子中，我们看到了多项式和样条在超出训练观测范围进行外推时的局限性。在某些情况下，例如具有季节性效应时，我们期望基础信号的周期性延续。此类效应可以使用周期样条进行建模，周期样条在第一个和最后一个节点处具有相等的函数值和相等的导数。在以下案例中，我们展示了在给定周期性附加信息的情况下，周期样条如何在训练数据范围内和范围外都提供更好的拟合。样条的周期是第一个和最后一个节点之间的距离，我们手动指定该距离。

周期样条对于自然周期特征（例如一年中的某一天）也很有用，因为边界节点的平滑性可以防止转换值的跳跃（例如从12月31日到1月1日）。对于这种自然周期特征或更一般的已知周期特征，建议通过手动设置节点将此信息显式传递给 SplineTransformer 。

def g(x):
    """通过周期样条插值进行逼近的函数。"""
    return np.sin(x) - 0.7 * np.cos(x * 3)


y_train = g(x_train)

# 将测试数据扩展到未来：
x_plot_ext = np.linspace(-1, 21, 200)
X_plot_ext = x_plot_ext[:, np.newaxis]

lw = 2
fig, ax = plt.subplots()
ax.set_prop_cycle(color=["black", "tomato", "teal"])
ax.plot(x_plot_ext, g(x_plot_ext), linewidth=lw, label="ground truth")
ax.scatter(x_train, y_train, label="training points")

for transformer, label in [
    (SplineTransformer(degree=3, n_knots=10), "spline"),
    (
        SplineTransformer(
            degree=3,
            knots=np.linspace(0, 2 * np.pi, 10)[:, None],
            extrapolation="periodic",
        ),
        "periodic spline",
    ),
]:
    model = make_pipeline(transformer, Ridge(alpha=1e-3))
    model.fit(X_train, y_train)
    y_plot_ext = model.predict(X_plot_ext)
    ax.plot(x_plot_ext, y_plot_ext, label=label)

ax.legend()
fig.show()

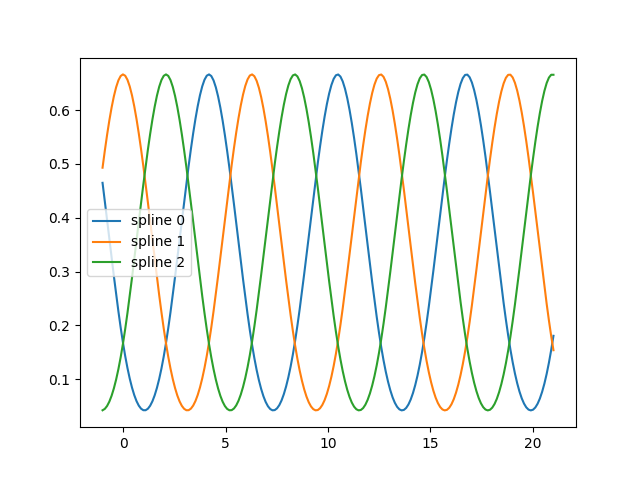
fig, ax = plt.subplots()
knots = np.linspace(0, 2 * np.pi, 4)
splt = SplineTransformer(knots=knots[:, None], degree=3, extrapolation="periodic").fit(
    X_train
)
ax.plot(x_plot_ext, splt.transform(X_plot_ext))
ax.legend(ax.lines, [f"spline {n}" for n in range(3)])
plt.show()