Note

Go to the end to download the full example code. or to run this example in your browser via Binder

使用KBinsDiscretizer离散连续特征#

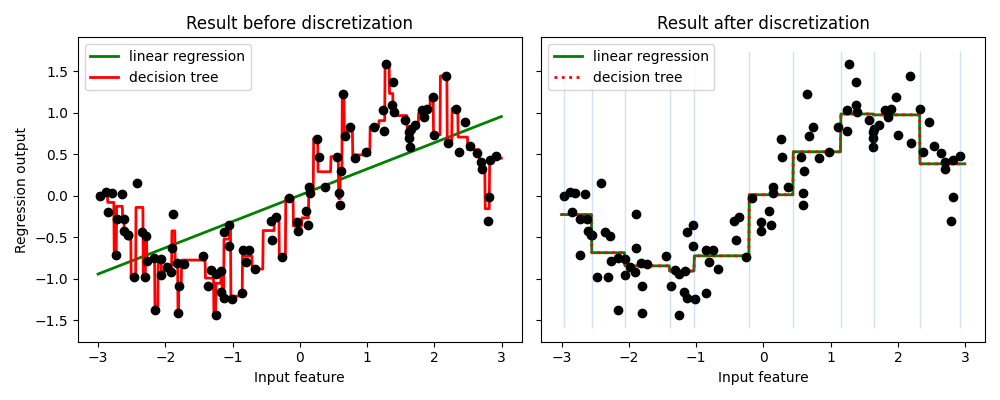
该示例比较了线性回归（线性模型）和决策树（基于树的模型）在对实值特征进行离散化前后的预测结果。

如离散化前的结果所示，线性模型构建速度快且相对易于解释，但只能建模线性关系，而决策树可以构建数据的更复杂模型。使线性模型在连续数据上更强大的一种方法是使用离散化（也称为分箱）。在示例中，我们对特征进行离散化并对转换后的数据进行独热编码。请注意，如果分箱不够宽，则可能会显著增加过拟合的风险，因此通常应在交叉验证下调整离散化参数。

离散化后，线性回归和决策树做出完全相同的预测。由于每个分箱内的特征是恒定的，任何模型都必须对分箱内的所有点预测相同的值。与离散化前的结果相比，线性模型变得更加灵活，而决策树变得不那么灵活。请注意，分箱特征对基于树的模型通常没有有益效果，因为这些模型可以在数据的任何地方进行分割。

Result before discretization, Result after discretization

# 作者：scikit-learn 开发者
# SPDX-License-Identifier: BSD-3-Clause

import matplotlib.pyplot as plt
import numpy as np

from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import KBinsDiscretizer
from sklearn.tree import DecisionTreeRegressor

# 构建数据集
rnd = np.random.RandomState(42)
X = rnd.uniform(-3, 3, size=100)
y = np.sin(X) + rnd.normal(size=len(X)) / 3
X = X.reshape(-1, 1)

# 使用KBinsDiscretizer对数据集进行转换
enc = KBinsDiscretizer(n_bins=10, encode="onehot")
X_binned = enc.fit_transform(X)

# 使用原始数据集进行预测
fig, (ax1, ax2) = plt.subplots(ncols=2, sharey=True, figsize=(10, 4))
line = np.linspace(-3, 3, 1000, endpoint=False).reshape(-1, 1)
reg = LinearRegression().fit(X, y)
ax1.plot(line, reg.predict(line), linewidth=2, color="green", label="linear regression")
reg = DecisionTreeRegressor(min_samples_split=3, random_state=0).fit(X, y)
ax1.plot(line, reg.predict(line), linewidth=2, color="red", label="decision tree")
ax1.plot(X[:, 0], y, "o", c="k")
ax1.legend(loc="best")
ax1.set_ylabel("Regression output")
ax1.set_xlabel("Input feature")
ax1.set_title("Result before discretization")

# 使用转换后的数据集进行预测
line_binned = enc.transform(line)
reg = LinearRegression().fit(X_binned, y)
ax2.plot(
    line,
    reg.predict(line_binned),
    linewidth=2,
    color="green",
    linestyle="-",
    label="linear regression",
)
reg = DecisionTreeRegressor(min_samples_split=3, random_state=0).fit(X_binned, y)
ax2.plot(
    line,
    reg.predict(line_binned),
    linewidth=2,
    color="red",
    linestyle=":",
    label="decision tree",
)
ax2.plot(X[:, 0], y, "o", c="k")
ax2.vlines(enc.bin_edges_[0], *plt.gca().get_ylim(), linewidth=1, alpha=0.2)
ax2.legend(loc="best")
ax2.set_xlabel("Input feature")
ax2.set_title("Result after discretization")

plt.tight_layout()
plt.show()