Note

Go to the end to download the full example code. or to run this example in your browser via Binder

多任务Lasso的联合特征选择#

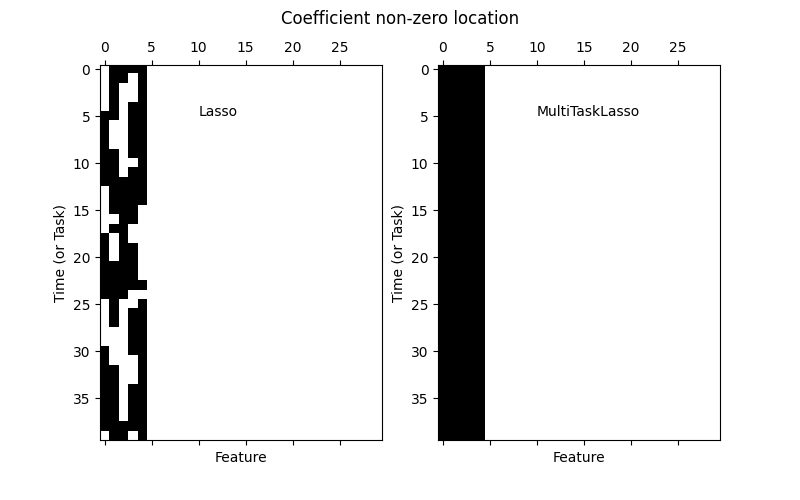
多任务Lasso允许联合拟合多个回归问题，强制所选特征在所有任务中保持一致。此示例模拟了序列测量，每个任务是一个时间点，相关特征在时间上幅度变化但保持相同。多任务Lasso强制在一个时间点选择的特征在所有时间点都被选择。这使得Lasso的特征选择更加稳定。

# 作者：scikit-learn 开发者
# SPDX 许可证标识符：BSD-3-Clause

生成数据#

import numpy as np

rng = np.random.RandomState(42)

# 生成一些具有随机频率和相位的正弦波的二维系数
n_samples, n_features, n_tasks = 100, 30, 40
n_relevant_features = 5
coef = np.zeros((n_tasks, n_features))
times = np.linspace(0, 2 * np.pi, n_tasks)
for k in range(n_relevant_features):
    coef[:, k] = np.sin((1.0 + rng.randn(1)) * times + 3 * rng.randn(1))

X = rng.randn(n_samples, n_features)
Y = np.dot(X, coef.T) + rng.randn(n_samples, n_tasks)

Fit models#

from sklearn.linear_model import Lasso, MultiTaskLasso

coef_lasso_ = np.array([Lasso(alpha=0.5).fit(X, y).coef_ for y in Y.T])
coef_multi_task_lasso_ = MultiTaskLasso(alpha=1.0).fit(X, Y).coef_

绘制支撑线和时间序列#

import matplotlib.pyplot as plt

fig = plt.figure(figsize=(8, 5))
plt.subplot(1, 2, 1)
plt.spy(coef_lasso_)
plt.xlabel("Feature")
plt.ylabel("Time (or Task)")
plt.text(10, 5, "Lasso")
plt.subplot(1, 2, 2)
plt.spy(coef_multi_task_lasso_)
plt.xlabel("Feature")
plt.ylabel("Time (or Task)")
plt.text(10, 5, "MultiTaskLasso")
fig.suptitle("Coefficient non-zero location")

feature_to_plot = 0
plt.figure()
lw = 2
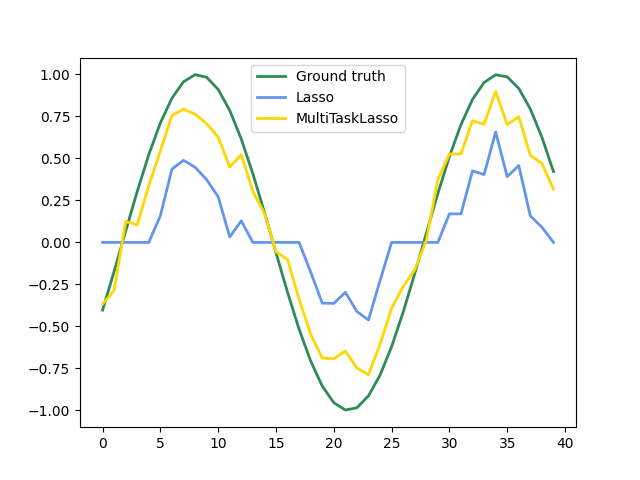
plt.plot(coef[:, feature_to_plot], color="seagreen", linewidth=lw, label="Ground truth")
plt.plot(
    coef_lasso_[:, feature_to_plot], color="cornflowerblue", linewidth=lw, label="Lasso"
)
plt.plot(
    coef_multi_task_lasso_[:, feature_to_plot],
    color="gold",
    linewidth=lw,
    label="MultiTaskLasso",
)
plt.legend(loc="upper center")
plt.axis("tight")
plt.ylim([-1.1, 1.1])
plt.show()