Note

Go to the end to download the full example code. or to run this example in your browser via Binder

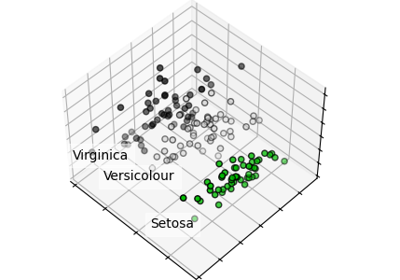
稀疏性示例：仅拟合特征1和特征2#

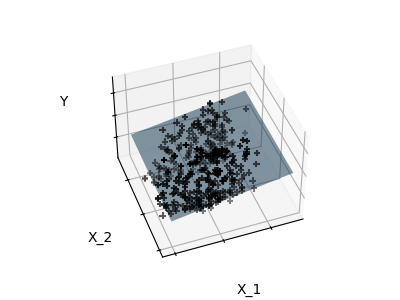
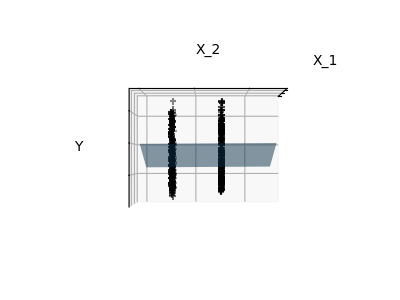
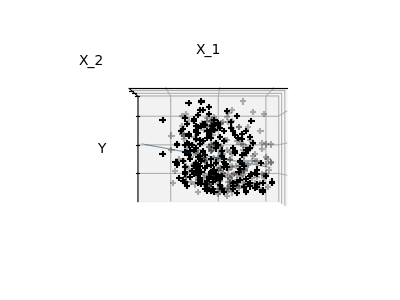
下图展示了对糖尿病数据集的特征1和特征2进行拟合的结果。尽管特征2在完整模型中具有较大的系数，但与仅使用特征1相比，它对 y 的贡献并不大。

# 代码来源：Gaël Varoquaux
# 由Jaques Grobler修改用于文档
# SPDX许可证标识符：BSD-3-Clause

首先，我们加载糖尿病数据集。

import numpy as np

from sklearn import datasets

X, y = datasets.load_diabetes(return_X_y=True)
indices = (0, 1)

X_train = X[:-20, indices]
X_test = X[-20:, indices]
y_train = y[:-20]
y_test = y[-20:]

接下来我们拟合一个线性回归模型。

from sklearn import linear_model

ols = linear_model.LinearRegression()
_ = ols.fit(X_train, y_train)

最后，我们从三个不同的视角绘制图形。

import matplotlib.pyplot as plt

# 未使用但需要的导入，用于在 matplotlib 版本小于 3.2 时进行 3D 投影
import mpl_toolkits.mplot3d  # noqa: F401


def plot_figs(fig_num, elev, azim, X_train, clf):
    fig = plt.figure(fig_num, figsize=(4, 3))
    plt.clf()
    ax = fig.add_subplot(111, projection="3d", elev=elev, azim=azim)

    ax.scatter(X_train[:, 0], X_train[:, 1], y_train, c="k", marker="+")
    ax.plot_surface(
        np.array([[-0.1, -0.1], [0.15, 0.15]]),
        np.array([[-0.1, 0.15], [-0.1, 0.15]]),
        clf.predict(
            np.array([[-0.1, -0.1, 0.15, 0.15], [-0.1, 0.15, -0.1, 0.15]]).T
        ).reshape((2, 2)),
        alpha=0.5,
    )
    ax.set_xlabel("X_1")
    ax.set_ylabel("X_2")
    ax.set_zlabel("Y")
    ax.xaxis.set_ticklabels([])
    ax.yaxis.set_ticklabels([])
    ax.zaxis.set_ticklabels([])


# 生成三个不同视角的不同图形
elev = 43.5
azim = -110
plot_figs(1, elev, azim, X_train, ols)

elev = -0.5
azim = 0
plot_figs(2, elev, azim, X_train, ols)

elev = -0.5
azim = 90
plot_figs(3, elev, azim, X_train, ols)

plt.show()