梯度提升回归

本示例演示了如何使用梯度提升从一组弱预测模型中生成一个预测模型。梯度提升可以用于回归和分类问题。在这里，我们将训练一个模型来解决糖尿病回归任务。我们将使用最小二乘损失和500棵深度为4的回归树，从:class:~sklearn.ensemble.GradientBoostingRegressor 中获得结果。

注意：对于较大的数据集（n_samples >= 10000），请参考:class:~sklearn.ensemble.HistGradientBoostingRegressor 。有关展示:class:~ensemble.HistGradientBoostingRegressor 其他优势的示例，请参见:ref:sphx_glr_auto_examples_ensemble_plot_hgbt_regression.py 。

# 作者：scikit-learn 开发者
# SPDX-License-Identifier: BSD-3-Clause

import matplotlib.pyplot as plt
import numpy as np

from sklearn import datasets, ensemble
from sklearn.inspection import permutation_importance
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split

加载数据

首先我们需要加载数据。

diabetes = datasets.load_diabetes()
X, y = diabetes.data, diabetes.target

数据预处理

接下来，我们将拆分数据集，使用90%进行训练，剩余部分用于测试。我们还将设置回归模型参数。你可以调整这些参数，观察结果的变化。

n_estimators ：将执行的提升阶段的数量。稍后，我们将绘制偏差与提升迭代次数的关系图。

max_depth ：限制树中的节点数量。最佳值取决于输入变量的相互作用。

min_samples_split ：拆分内部节点所需的最小样本数量。

learning_rate : 每棵树的贡献将缩减多少。

loss ：要优化的损失函数。在这种情况下使用的是最小二乘函数，不过还有许多其他选项（参见：GradientBoostingRegressor ）。

X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.1, random_state=13
)

params = {
    "n_estimators": 500,
    "max_depth": 4,
    "min_samples_split": 5,
    "learning_rate": 0.01,
    "loss": "squared_error",
}

拟合回归模型

现在我们将初始化梯度提升回归器并用我们的训练数据进行拟合。我们还将查看测试数据的均方误差。

reg = ensemble.GradientBoostingRegressor(**params)
reg.fit(X_train, y_train)

mse = mean_squared_error(y_test, reg.predict(X_test))
print("The mean squared error (MSE) on test set: {:.4f}".format(mse))

The mean squared error (MSE) on test set: 3027.4544

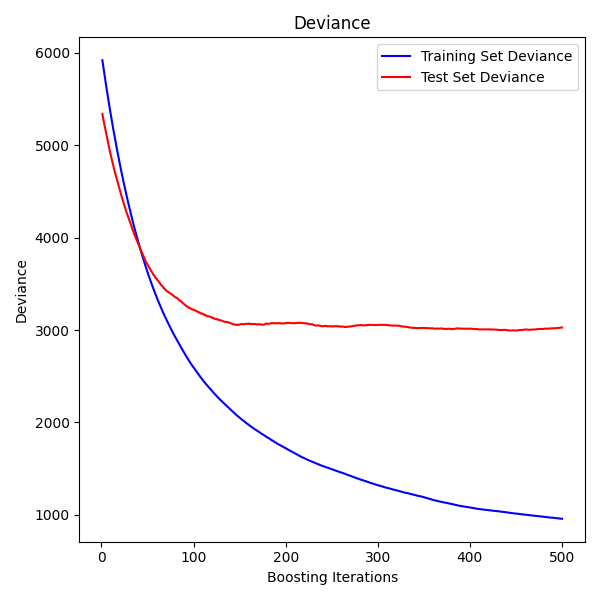
绘制训练偏差图

最后，我们将对结果进行可视化。为此，我们将首先计算测试集偏差，然后将其与提升迭代次数进行对比绘图。

test_score = np.zeros((params["n_estimators"],), dtype=np.float64)
for i, y_pred in enumerate(reg.staged_predict(X_test)):
    test_score[i] = mean_squared_error(y_test, y_pred)

fig = plt.figure(figsize=(6, 6))
plt.subplot(1, 1, 1)
plt.title("Deviance")
plt.plot(
    np.arange(params["n_estimators"]) + 1,
    reg.train_score_,
    "b-",
    label="Training Set Deviance",
)
plt.plot(
    np.arange(params["n_estimators"]) + 1, test_score, "r-", label="Test Set Deviance"
)
plt.legend(loc="upper right")
plt.xlabel("Boosting Iterations")
plt.ylabel("Deviance")
fig.tight_layout()
plt.show()

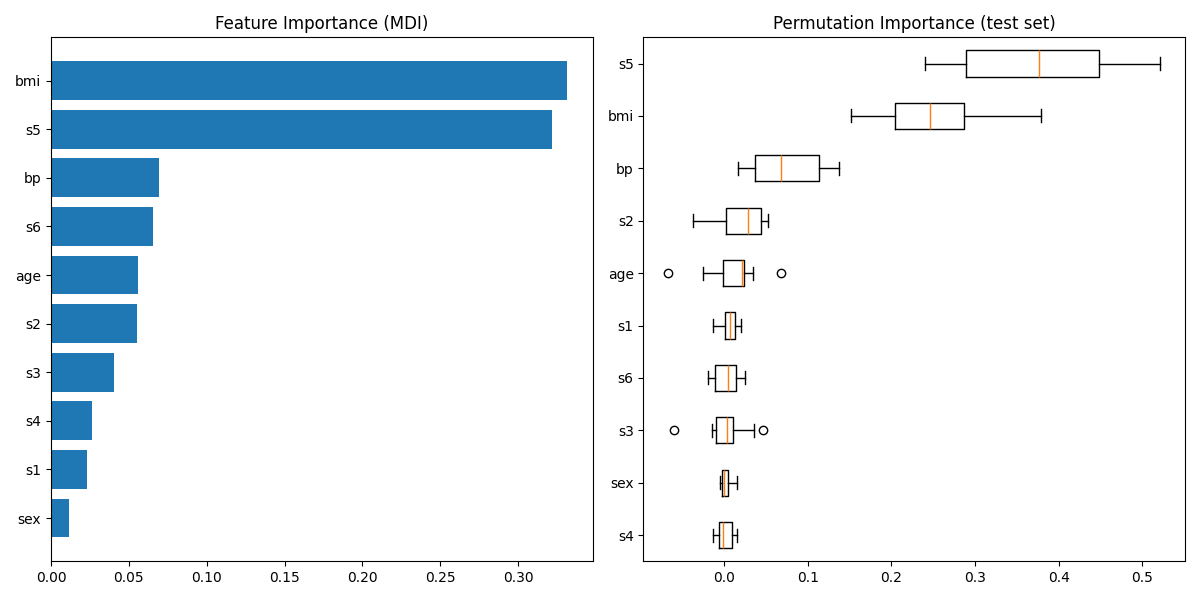
绘制特征重要性

注意，对于 高基数 特征（具有许多唯一值），基于杂质的特征重要性可能会产生误导。作为替代，可以在保留的测试集上计算 reg 的置换重要性。更多详情请参见 排列特征重要性 。

对于这个例子，基于不纯度的方法和置换方法识别出了相同的两个强预测特征，但顺序不同。第三个最具预测性的特征 “bp” 对于这两种方法也是相同的。其余特征的预测性较低，并且置换图的误差条显示它们与0重叠。

feature_importance = reg.feature_importances_
sorted_idx = np.argsort(feature_importance)
pos = np.arange(sorted_idx.shape[0]) + 0.5
fig = plt.figure(figsize=(12, 6))
plt.subplot(1, 2, 1)
plt.barh(pos, feature_importance[sorted_idx], align="center")
plt.yticks(pos, np.array(diabetes.feature_names)[sorted_idx])
plt.title("Feature Importance (MDI)")

result = permutation_importance(
    reg, X_test, y_test, n_repeats=10, random_state=42, n_jobs=2
)
sorted_idx = result.importances_mean.argsort()
plt.subplot(1, 2, 2)
plt.boxplot(
    result.importances[sorted_idx].T,
    vert=False,
    labels=np.array(diabetes.feature_names)[sorted_idx],
)
plt.title("Permutation Importance (test set)")
fig.tight_layout()
plt.show()

/app/scikit-learn-main-origin/examples/ensemble/plot_gradient_boosting_regression.py:123: MatplotlibDeprecationWarning:

The 'labels' parameter of boxplot() has been renamed 'tick_labels' since Matplotlib 3.9; support for the old name will be dropped in 3.11.

Related examples

梯度提升袋外估计

梯度提升袋外估计

使用贝叶斯岭回归进行曲线拟合

使用贝叶斯岭回归进行曲线拟合

使用KBinsDiscretizer离散连续特征

使用KBinsDiscretizer离散连续特征

梯度提升中的提前停止

梯度提升中的提前停止