Note
Go to the end to download the full example code. or to run this example in your browser via Binder
绘制学习曲线和检查模型的可扩展性#
在这个示例中,我们展示了如何使用类
LearningCurveDisplay 来轻松绘制学习曲线。此外,我们对朴素贝叶斯和SVM分类器获得的学习曲线进行了解释。
然后,我们通过观察这些预测模型的计算成本,而不仅仅是它们的统计准确性,来探索并得出关于它们可扩展性的一些结论。
学习曲线#
学习曲线展示了在训练过程中增加更多样本的效果。通过检查模型在训练得分和测试得分方面的统计性能来描绘这种效果。
在这里,我们使用数字数据集计算朴素贝叶斯分类器和带有RBF核的SVM分类器的学习曲线。
from sklearn.datasets import load_digits
from sklearn.naive_bayes import GaussianNB
from sklearn.svm import SVC
X, y = load_digits(return_X_y=True)
naive_bayes = GaussianNB()
svc = SVC(kernel="rbf", gamma=0.001)
from_estimator 方法在给定数据集和预测模型的情况下显示学习曲线。为了估计分数的不确定性,该方法使用了交叉验证程序。
import matplotlib.pyplot as plt
import numpy as np
from sklearn.model_selection import LearningCurveDisplay, ShuffleSplit
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(10, 6), sharey=True)
common_params = {
"X": X,
"y": y,
"train_sizes": np.linspace(0.1, 1.0, 5),
"cv": ShuffleSplit(n_splits=50, test_size=0.2, random_state=0),
"score_type": "both",
"n_jobs": 4,
"line_kw": {"marker": "o"},
"std_display_style": "fill_between",
"score_name": "Accuracy",
}
for ax_idx, estimator in enumerate([naive_bayes, svc]):
LearningCurveDisplay.from_estimator(estimator, **common_params, ax=ax[ax_idx])
handles, label = ax[ax_idx].get_legend_handles_labels()
ax[ax_idx].legend(handles[:2], ["Training Score", "Test Score"])
ax[ax_idx].set_title(f"Learning Curve for {estimator.__class__.__name__}")
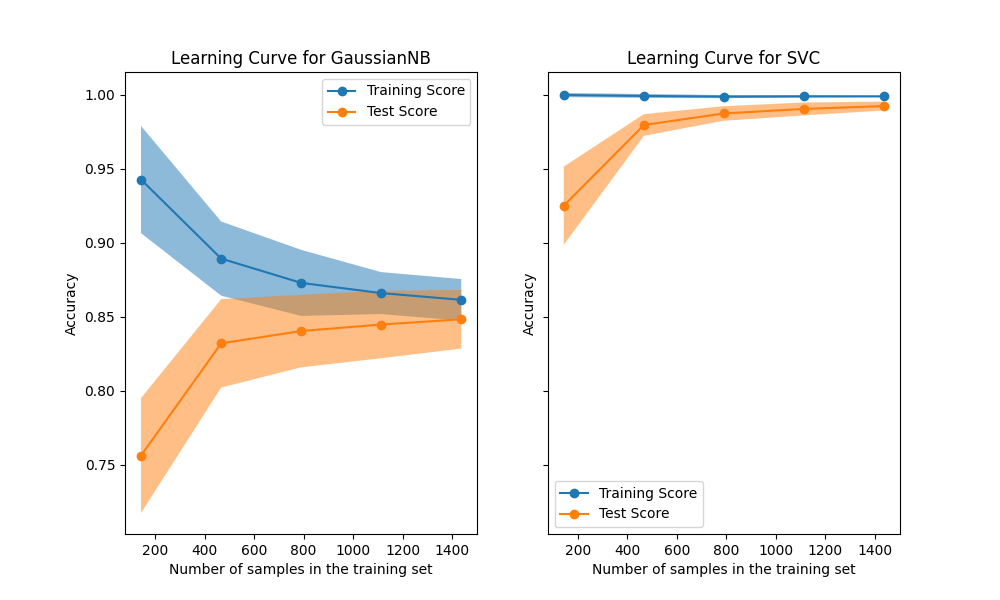
我们首先分析朴素贝叶斯分类器的学习曲线。它的形状在更复杂的数据集中也很常见:在使用少量样本进行训练时,训练得分非常高,而随着样本数量的增加,训练得分会下降;而测试得分在开始时非常低,随着样本的增加而上升。当所有样本都用于训练时,训练和测试得分变得更加真实。
我们看到使用RBF核的SVM分类器的另一条典型学习曲线。无论训练集的大小如何,训练得分始终保持在较高水平。另一方面,测试得分随着训练数据集的大小增加而提高。实际上,它增加到某个点后达到一个平台。观察到这样的平台表明,获取新数据来训练模型可能没有用,因为模型的泛化性能不会再提高了。
复杂度分析#
除了这些学习曲线之外,还可以从训练和评分时间的角度来看预测模型的可扩展性。
LearningCurveDisplay 类不提供此类信息。我们需要改用 learning_curve 函数并手动绘制图表。
from sklearn.model_selection import learning_curve
common_params = {
"X": X,
"y": y,
"train_sizes": np.linspace(0.1, 1.0, 5),
"cv": ShuffleSplit(n_splits=50, test_size=0.2, random_state=0),
"n_jobs": 4,
"return_times": True,
}
train_sizes, _, test_scores_nb, fit_times_nb, score_times_nb = learning_curve(
naive_bayes, **common_params
)
train_sizes, _, test_scores_svm, fit_times_svm, score_times_svm = learning_curve(
svc, **common_params
)
fig, ax = plt.subplots(nrows=2, ncols=2, figsize=(16, 12), sharex=True)
for ax_idx, (fit_times, score_times, estimator) in enumerate(
zip(
[fit_times_nb, fit_times_svm],
[score_times_nb, score_times_svm],
[naive_bayes, svc],
)
):
# 关于拟合时间的可扩展性
ax[0, ax_idx].plot(train_sizes, fit_times.mean(axis=1), "o-")
ax[0, ax_idx].fill_between(
train_sizes,
fit_times.mean(axis=1) - fit_times.std(axis=1),
fit_times.mean(axis=1) + fit_times.std(axis=1),
alpha=0.3,
)
ax[0, ax_idx].set_ylabel("Fit time (s)")
ax[0, ax_idx].set_title(
f"Scalability of the {estimator.__class__.__name__} classifier"
)
# 关于评分时间的可扩展性
ax[1, ax_idx].plot(train_sizes, score_times.mean(axis=1), "o-")
ax[1, ax_idx].fill_between(
train_sizes,
score_times.mean(axis=1) - score_times.std(axis=1),
score_times.mean(axis=1) + score_times.std(axis=1),
alpha=0.3,
)
ax[1, ax_idx].set_ylabel("Score time (s)")
ax[1, ax_idx].set_xlabel("Number of training samples")
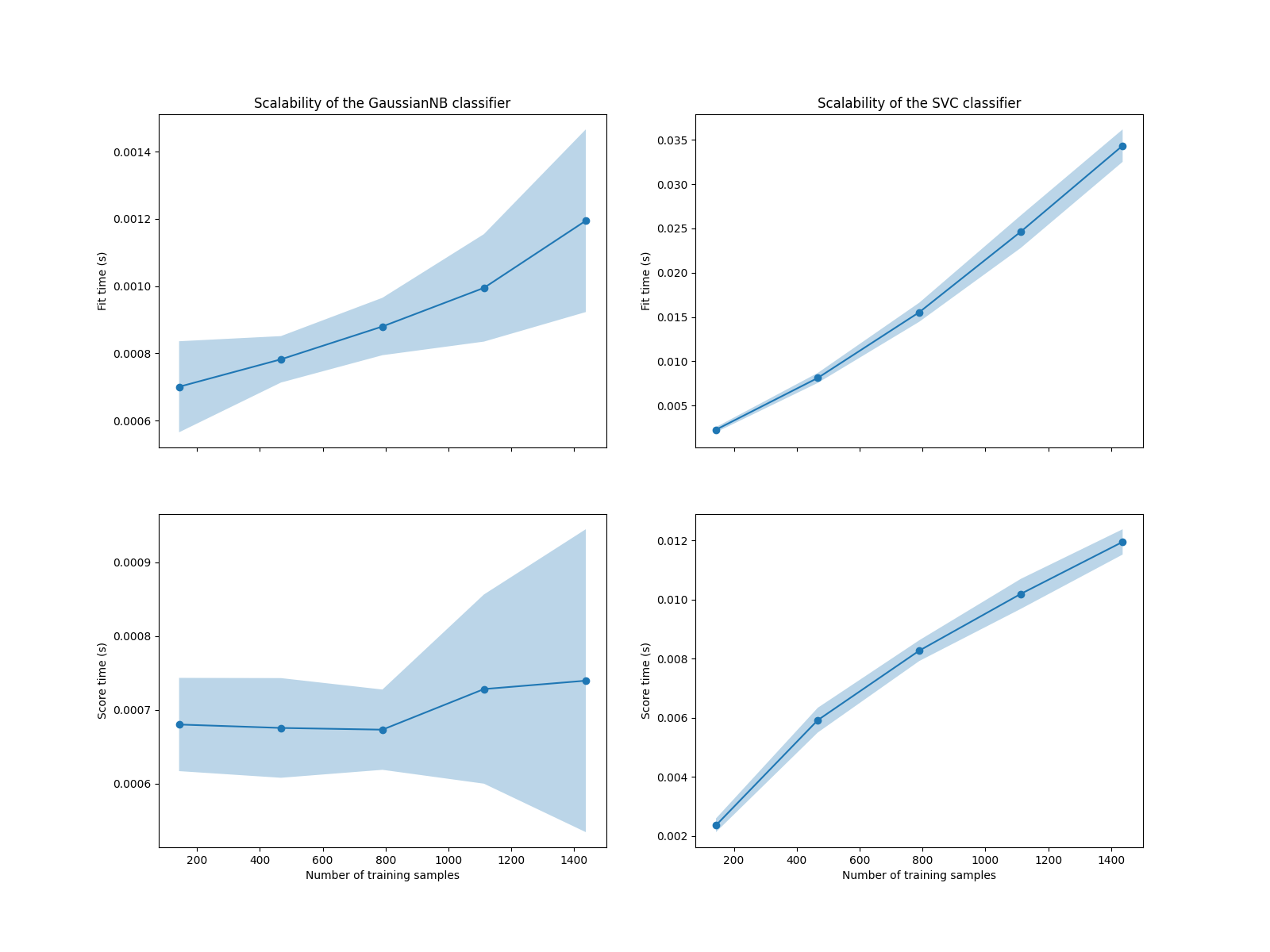
我们看到 SVM 和朴素贝叶斯分类器的可扩展性非常不同。SVM 分类器在拟合和评分时的复杂度会随着样本数量的增加而迅速增加。实际上,已知该分类器的拟合时间复杂度与样本数量呈超过二次方的关系,这使得它难以扩展到超过几万个样本的数据集。相比之下,朴素贝叶斯分类器在拟合和评分时的复杂度较低,因此扩展性要好得多。
随后,我们可以检查训练时间增加与交叉验证得分之间的权衡。
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(16, 6))
for ax_idx, (fit_times, test_scores, estimator) in enumerate(
zip(
[fit_times_nb, fit_times_svm],
[test_scores_nb, test_scores_svm],
[naive_bayes, svc],
)
):
ax[ax_idx].plot(fit_times.mean(axis=1), test_scores.mean(axis=1), "o-")
ax[ax_idx].fill_between(
fit_times.mean(axis=1),
test_scores.mean(axis=1) - test_scores.std(axis=1),
test_scores.mean(axis=1) + test_scores.std(axis=1),
alpha=0.3,
)
ax[ax_idx].set_ylabel("Accuracy")
ax[ax_idx].set_xlabel("Fit time (s)")
ax[ax_idx].set_title(
f"Performance of the {estimator.__class__.__name__} classifier"
)
plt.show()
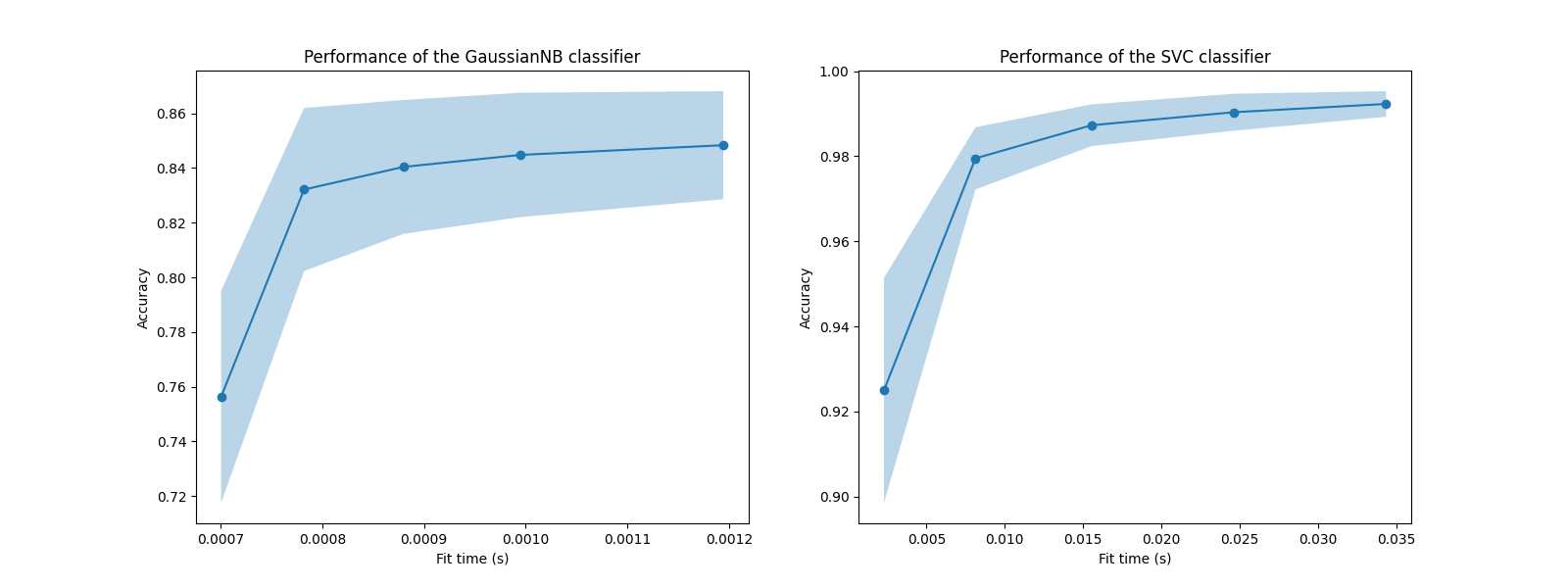
在这些图中,我们可以寻找交叉验证得分不再增加且仅训练时间增加的拐点。
Total running time of the script: (0 minutes 8.693 seconds)
Related examples