Note
Go to the end to download the full example code. or to run this example in your browser via Binder
类似然比率用于衡量分类性能#
本示例演示了 class_likelihood_ratios 函数,该函数计算正似然比和负似然比 ( LR+ , LR- ),以评估二元分类器的预测能力。正如我们将看到的,这些指标与测试集中类的比例无关,这使得它们在研究数据与目标应用的数据类比例不同的情况下非常有用。
一个典型的应用是医学中的病例对照研究,其中类几乎是平衡的,而普通人群中类严重不平衡。在这种应用中,个体患有目标疾病的测试前概率可以选择为患病率,即某特定人群中被发现患有某种疾病的比例。测试后概率则表示在测试结果为阳性的情况下,疾病确实存在的概率。
在本示例中,我们首先讨论由 类别似然比 给出的测试前和测试后几率之间的关系。然后我们在一些受控场景中评估它们的行为。在最后一部分中,我们将它们绘制为阳性类患病率的函数。
# 作者: Arturo Amor <david-arturo.amor-quiroz@inria.fr>
# Olivier Grisel <olivier.grisel@ensta.org>
测试前与测试后分析#
假设我们有一个包含生理测量值 X 的受试者群体,这些测量值有望作为疾病的间接生物标志物,以及实际的疾病指标 y (真实情况)。群体中的大多数人不携带疾病,但少数人(在这种情况下大约10%)携带疾病:
from sklearn.datasets import make_classification
X, y = make_classification(n_samples=10_000, weights=[0.9, 0.1], random_state=0)
print(f"Percentage of people carrying the disease: {100*y.mean():.2f}%")
Percentage of people carrying the disease: 10.37%
一个机器学习模型被构建用于诊断一个具有某些生理测量值的人是否可能携带感兴趣的疾病。为了评估该模型,我们需要在一个保留的测试集上评估其性能:
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
然后我们可以拟合我们的诊断模型,并计算阳性似然比,以评估该分类器作为疾病诊断工具的有效性:
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import class_likelihood_ratios
estimator = LogisticRegression().fit(X_train, y_train)
y_pred = estimator.predict(X_test)
pos_LR, neg_LR = class_likelihood_ratios(y_test, y_pred)
print(f"LR+: {pos_LR:.3f}")
LR+: 12.617
由于正类似然比远大于1.0,这意味着基于机器学习的诊断工具是有用的:在测试结果为阳性的情况下,病情确实存在的事后几率比事前几率大12倍以上。
交叉验证似然比#
我们评估在某些特定情况下类别似然比测量的变异性。
import pandas as pd
def scoring(estimator, X, y):
y_pred = estimator.predict(X)
pos_lr, neg_lr = class_likelihood_ratios(y, y_pred, raise_warning=False)
return {"positive_likelihood_ratio": pos_lr, "negative_likelihood_ratio": neg_lr}
def extract_score(cv_results):
lr = pd.DataFrame(
{
"positive": cv_results["test_positive_likelihood_ratio"],
"negative": cv_results["test_negative_likelihood_ratio"],
}
)
return lr.aggregate(["mean", "std"])
我们首先验证在上一节中使用默认超参数的 LogisticRegression 模型。
from sklearn.model_selection import cross_validate
estimator = LogisticRegression()
extract_score(cross_validate(estimator, X, y, scoring=scoring, cv=10))
我们确认该模型是有用的:测试后的赔率是测试前赔率的12到20倍。
相反,让我们考虑一个虚拟模型,该模型将输出与训练集中平均疾病流行率相似概率的随机预测:
from sklearn.dummy import DummyClassifier
estimator = DummyClassifier(strategy="stratified", random_state=1234)
extract_score(cross_validate(estimator, X, y, scoring=scoring, cv=10))
在这里,两个类别的似然比都接近1.0,这使得该分类器作为改进疾病检测的诊断工具毫无用处。
另一种虚拟模型的选项是始终预测最频繁的类别,在这种情况下是“无病”。
estimator = DummyClassifier(strategy="most_frequent")
extract_score(cross_validate(estimator, X, y, scoring=scoring, cv=10))
没有正预测意味着不会有真正例(true positives)或假正例(false positives),导致 LR+ 未定义,这绝不应被解释为无限的 LR+ (即分类器完美识别正例)。在这种情况下,class_likelihood_ratios 函数默认返回 nan 并发出警告。实际上, LR- 的值帮助我们排除这个模型。
在对样本量少且高度不平衡的数据进行交叉验证时,可能会出现类似的情况:某些折叠中没有患病样本,因此在测试时不会输出真正例或假阴性。从数学上讲,这会导致无限的 LR+ ,这也不应被解释为模型完美地识别了阳性病例。这种情况会导致估计的似然比的方差更高,但仍可以解释为患病后测试几率的增加。
estimator = LogisticRegression()
X, y = make_classification(n_samples=300, weights=[0.9, 0.1], random_state=0)
extract_score(cross_validate(estimator, X, y, scoring=scoring, cv=10))
对流行率的不变性#
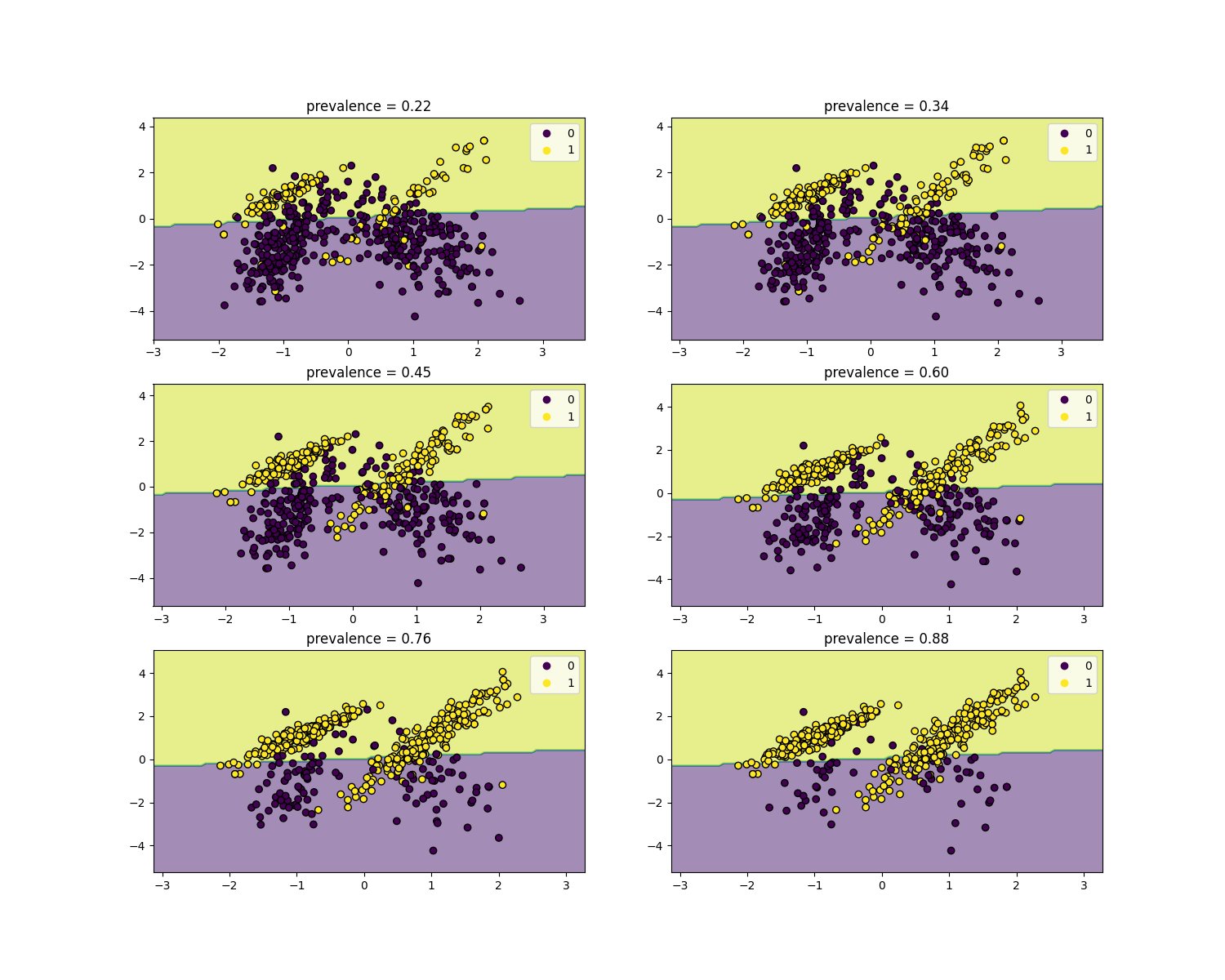
似然比与疾病流行率无关,可以在不同人群之间外推,而不考虑任何可能的类别不平衡, 只要对所有人群应用相同的模型 。请注意,在下面的图中, **决策边界是恒定的**(有关不平衡类别的边界决策研究,请参见:ref:sphx_glr_auto_examples_svm_plot_separating_hyperplane_unbalanced.py )。
我们在患病率为50%的病例对照研究中训练一个 LogisticRegression 基础模型。然后在患病率不同的人群中进行评估。我们使用 make_classification 函数来确保数据生成过程始终与下图所示相同。标签 1 对应于阳性类别“疾病”,而标签 0 代表“无疾病”。
from collections import defaultdict
import matplotlib.pyplot as plt
import numpy as np
from sklearn.inspection import DecisionBoundaryDisplay
populations = defaultdict(list)
common_params = {
"n_samples": 10_000,
"n_features": 2,
"n_informative": 2,
"n_redundant": 0,
"random_state": 0,
}
weights = np.linspace(0.1, 0.8, 6)
weights = weights[::-1]
# 在平衡类上拟合和评估基础模型
X, y = make_classification(**common_params, weights=[0.5, 0.5])
estimator = LogisticRegression().fit(X, y)
lr_base = extract_score(cross_validate(estimator, X, y, scoring=scoring, cv=10))
pos_lr_base, pos_lr_base_std = lr_base["positive"].values
neg_lr_base, neg_lr_base_std = lr_base["negative"].values
我们现在将展示每个流行水平的决策边界。请注意,我们只绘制了原始数据的一个子集,以更好地评估线性模型的决策边界。
fig, axs = plt.subplots(nrows=3, ncols=2, figsize=(15, 12))
for ax, (n, weight) in zip(axs.ravel(), enumerate(weights)):
X, y = make_classification(
**common_params,
weights=[weight, 1 - weight],
)
prevalence = y.mean()
populations["prevalence"].append(prevalence)
populations["X"].append(X)
populations["y"].append(y)
# 下采样以进行绘图
rng = np.random.RandomState(1)
plot_indices = rng.choice(np.arange(X.shape[0]), size=500, replace=True)
X_plot, y_plot = X[plot_indices], y[plot_indices]
# 绘制基础模型在不同流行率下的固定决策边界
disp = DecisionBoundaryDisplay.from_estimator(
estimator,
X_plot,
response_method="predict",
alpha=0.5,
ax=ax,
)
scatter = disp.ax_.scatter(X_plot[:, 0], X_plot[:, 1], c=y_plot, edgecolor="k")
disp.ax_.set_title(f"prevalence = {y_plot.mean():.2f}")
disp.ax_.legend(*scatter.legend_elements())
我们定义了一个用于自举的方法。
def scoring_on_bootstrap(estimator, X, y, rng, n_bootstrap=100):
results_for_prevalence = defaultdict(list)
for _ in range(n_bootstrap):
bootstrap_indices = rng.choice(
np.arange(X.shape[0]), size=X.shape[0], replace=True
)
for key, value in scoring(
estimator, X[bootstrap_indices], y[bootstrap_indices]
).items():
results_for_prevalence[key].append(value)
return pd.DataFrame(results_for_prevalence)
我们使用自举法对每个流行率的基础模型进行评分。
results = defaultdict(list)
n_bootstrap = 100
rng = np.random.default_rng(seed=0)
for prevalence, X, y in zip(
populations["prevalence"], populations["X"], populations["y"]
):
results_for_prevalence = scoring_on_bootstrap(
estimator, X, y, rng, n_bootstrap=n_bootstrap
)
results["prevalence"].append(prevalence)
results["metrics"].append(
results_for_prevalence.aggregate(["mean", "std"]).unstack()
)
results = pd.DataFrame(results["metrics"], index=results["prevalence"])
results.index.name = "prevalence"
results
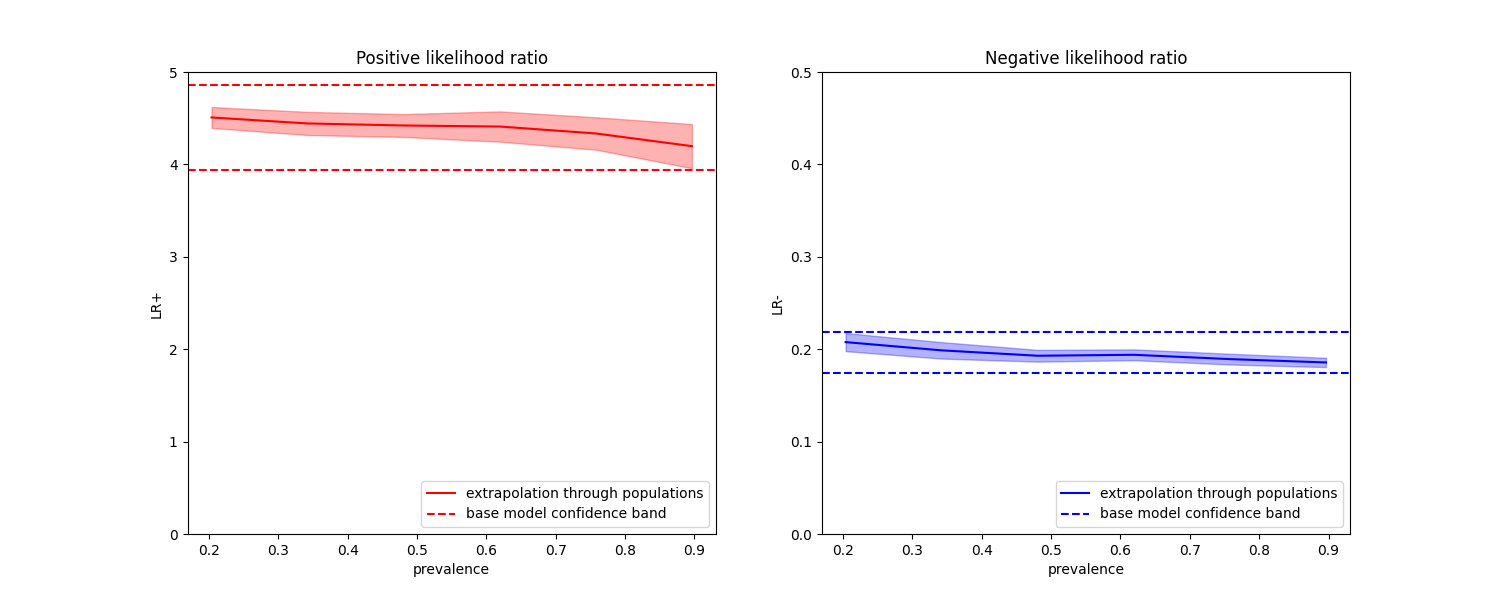
在下图中,我们观察到使用不同流行率重新计算的类别似然比确实在一个标准差范围内保持恒定,与在平衡类别下计算的结果一致。
fig, (ax1, ax2) = plt.subplots(nrows=1, ncols=2, figsize=(15, 6))
results["positive_likelihood_ratio"]["mean"].plot(
ax=ax1, color="r", label="extrapolation through populations"
)
ax1.axhline(y=pos_lr_base + pos_lr_base_std, color="r", linestyle="--")
ax1.axhline(
y=pos_lr_base - pos_lr_base_std,
color="r",
linestyle="--",
label="base model confidence band",
)
ax1.fill_between(
results.index,
results["positive_likelihood_ratio"]["mean"]
- results["positive_likelihood_ratio"]["std"],
results["positive_likelihood_ratio"]["mean"]
+ results["positive_likelihood_ratio"]["std"],
color="r",
alpha=0.3,
)
ax1.set(
title="Positive likelihood ratio",
ylabel="LR+",
ylim=[0, 5],
)
ax1.legend(loc="lower right")
ax2 = results["negative_likelihood_ratio"]["mean"].plot(
ax=ax2, color="b", label="extrapolation through populations"
)
ax2.axhline(y=neg_lr_base + neg_lr_base_std, color="b", linestyle="--")
ax2.axhline(
y=neg_lr_base - neg_lr_base_std,
color="b",
linestyle="--",
label="base model confidence band",
)
ax2.fill_between(
results.index,
results["negative_likelihood_ratio"]["mean"]
- results["negative_likelihood_ratio"]["std"],
results["negative_likelihood_ratio"]["mean"]
+ results["negative_likelihood_ratio"]["std"],
color="b",
alpha=0.3,
)
ax2.set(
title="Negative likelihood ratio",
ylabel="LR-",
ylim=[0, 0.5],
)
ax2.legend(loc="lower right")
plt.show()
Total running time of the script: (0 minutes 0.938 seconds)
Related examples
sphx_glr_auto_examples_model_selection_plot_successive_halving_iterations.py